【线段树】【P3740】 [HAOI2014]贴海报

传送门

Description

　　Bytetown城市要进行市长竞选，所有的选民可以畅所欲言地对竞选市长的候选人发表言论。为了统一管理，城市委员会为选民准备了一个张贴海报的electoral墙。

张贴规则如下：

1. electoral墙是一个长度为N个单位的长方形，每个单位记为一个格子；

2. 所有张贴的海报的高度必须与electoral墙的高度一致的；

3. 每张海报以“A B”表示，即从第A个格子到第B个格子张贴海报；

4. 后贴的海报可以覆盖前面已贴的海报或部分海报。

现在请你判断，张贴完所有海报后，在electoral墙上还可以看见多少张海报。

Input

　　第一行： N M 分别表示electoral墙的长度和海报个数

　　接下来M行: Ai Bi 表示每张海报张贴的位置

Output

　　输出贴完所有海报后，在electoral墙上还可以看见的海报数。

Sample Input

100 5
1 4
2 6
8 10
3 4
7 10

Sample Output

4

Hint　

　　10<= N <= 10000000 1<=M<=1000 1<= Ai <= Bi <=10000000

　　所有的数据都是整数。数据之间有一个空格

Solution

　　考虑暴力修改 上界复杂度将达到O(nm)。显然扯淡。

　　考虑进行优化。由于是对区间操作。最后输出答案也相当于对区间[1,n]进行询问，于是自然想到对区间操作最拿手的线段树。

　　如果在线修改，记录区间上有几个广告，以及区间上广告是否覆盖完全（即最右侧的广告在区间外是否还有一块），合并时f[p]=f[dp]+f[ddp](+1)，会产生问题：如样例图片：

　　　　　　　　　　

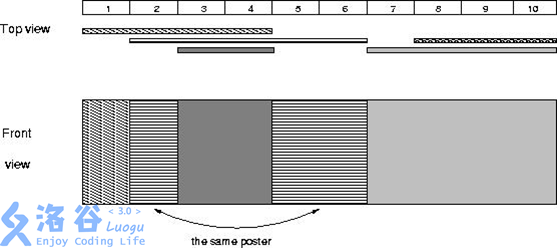
观察样例中间被英文标出的地方，使用上述算法，改区间会被判定为有三个广告。但事实上只有两个，因为是上面覆盖了下面的一部分。

　　如何解决此问题？考虑广告数量太大无法状压，但不强制在线，于是我们把广告都读进来，倒序插入。因为较早贴上的广告显然无法影响到后面的广告。这里再次使用了阶段划分和无后效性的思想。对于一个区间，如果已经被提前计算的广告完全覆盖，则直接return。一个广告能被看见，当且仅当他能覆盖一个独立的区间。至此，问题得解。

Code

#include<cstdio>
#include<algorithm>
#define ci const int
#define maxn 10000010
#define maxt 40000010

inline void qr(int &x) {
    char ch=getchar(),last=' ';
    while(ch>'9'||ch<'0') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9')    x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    if(last=='-')    x=-x;
}

inline int max(const int &a,const int &b) {if(a>b) return a;return b;}
inline int min(const int &a,const int &b) {if(a<b) return a;return b;}
inline int abs(const int &a) {if(a>=0) return a;return -a;}

inline void swap(int &a,int &b) {int temp=a;a=b;b=temp;}

int n,m,a,b,cnt;

bool tree[maxt],judge;

struct M {
    int l,r;
};
M MU[maxn];

void change(ci l,ci r,ci p,ci aiml,ci aimr) {
    if(l>r) return;
    if(l>aimr||r<aiml) return;
    if(l>=aiml&&r<=aimr) {if(!tree[p]) tree[p]=judge=true;return;}
    if(tree[p])    return;
    int mid=(l+r)>>1,dp=p<<1,ddp=dp|1;
    change(l,mid,dp,aiml,aimr);change(mid+1,r,ddp,aiml,aimr);
    tree[p]=tree[dp]&&tree[ddp];
}

int main() {
    qr(n);qr(m);
    for(int i=1;i<=m;++i) {qr(MU[i].l);qr(MU[i].r);}
    do {
        judge=false;
        change(1,n,1,MU[m].l,MU[m].r);
        if(judge) ++cnt;
    } while(--m);
    printf("%d
",cnt);
    return 0;
}

Summary

　　1、阶段划分是做任何题十分有力的工具，除开DP外，也要时刻应用。
　　2、在线难以处理时，考虑离线。正序难以处理时，考虑倒序。无序难以处理时，考虑有序。因为后者往往在一定程度上满足无后效性。