B [yLOI2019] 梅深不见冬
Background
风,吹起梅岭的深冬;霜,如惊涛一样汹涌;雪,飘落后把所有烧成空,
像这场,捕捉不到的梦。
醒来时已是多年之久,宫门铜环才长了铁锈,
也开始生出离愁。
——银临《梅深不见冬》
Description
给定一棵 (n) 个节点的树,在树上行走,每次要么选择一个没有到达过的子节点,要么返回父节点。想要在一个节点 (u) 放上梅花当且仅当 (u) 的任意子节点 (v) 都被放上了 (w_v) 朵梅花。在任意时刻可以收回任意节点的梅花。对于每个节点,求如果想在这个节点放梅花,则至少需要准备多少梅花。
Limitations
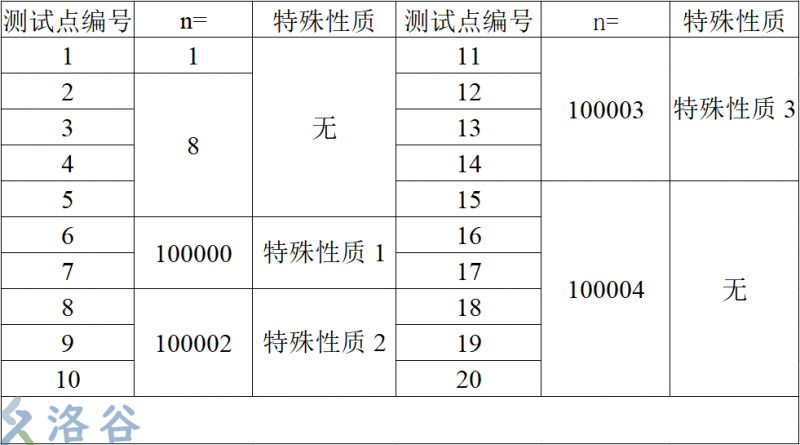
特殊性质1:每个节点的孩子结点个数不超过 (2)
特殊性质2:每个节点的孩子节点个数不超过 (5)
特殊性质3:任意一个节点到根的路径上的点数不超过 (3),也即树高不超过 (3)
对于 (100\%) 的数据,保证 (1 leq w_i leq 1000)
Solution
测试点 (1):
只有一个节点,输出 (w_1) 即可。期望得分 (5~pts)
测试点 (2~sim 5):
爆搜一个行走的顺序,然后可以 (O(n)) 判断是否合法。时间复杂度 (O(n! imes n)),期望得分 (20~pts)
测试点 (6~sim~7):
注意到题目所规定的走法相当于按照树的某个dfs序走,即离开某个节点时必须遍历完它的子树,否则子树中一旦有一个节点没有被遍历到,则永远无法返回这个节点。
如果设在点 (u) 上放上 (w_u) 朵梅花最少需要 (ans_u) 朵梅花的话,考虑对于 (u) 的两个孩子 (x,~y),如果先走 (x),那么首先需要准备 (ans_x) 朵梅花,放上了 (w_x) 朵梅花,剩余了 (ans_x - w_x) 朵花,再走 (y),需要准备 (ans_y) 朵花,当前有 (ans_x - w_x),则需要额外准备 (max(ans_y - ans_x + w_x, 0)) 朵花。先走 (y) 的情况类似,比较一下哪种情况更优即可。
时间复杂度 (O(n)),期望得分 (10~pts)
测试点 (8~sim 10):
孩子节点个数不超过 (5),于是爆搜一下走哪个孩子的顺序,用类似子任务 (3) 的方法统计,然后取最优的即可。
时间复杂度 (O(n imes x!)),其中 (x) 为最大的节点孩子个数。期望得分 (15~pts)
测试点 (11~sim 14):
树高不超过 (3),考虑第 (3) 层的节点,答案显然是他们自身的权值,第二层的节点,答案是第三层的权值和。
对于第一层的根节点 (u),考虑放满他的孩子的花费和在这个节点上放梅花的花费的关系:
如果放满它的孩子花费为 (c),它的孩子的权值和为 (W),则会剩余 (rest = c - W) 朵梅花,由于 (W) 是个常量,(rest) 与 (c) 正相关。考虑当 (w_u > rest) 时,需要额外花费 (w_u - rest) 元,花费为 (w_u - rest + rest = w_u) 元,当 (w_u leq rest) 时,花费 (rest) 元。由此可以发现,当 (rest) 减小时,所需要的花费不会增大。又因为 (rest) 与 (c) 正相关,因此放满它的孩子的花费变地,在这个节点上放梅花的花费不会增加。因此最小化放满它孩子的花费即可得到答案。
对于一个节点 (x),设往这个节点上放上梅花至少需要准备 (ans_x) 朵梅花,而 (x) 的权值为 (w_x),我们的问题是选择一个最优的放梅花的序列,使得最终需要准备的梅花最小。这个问题的答案是按照 (ans_x - w_x) 的不升序排序即可。
考虑证明这个结论:
设有两个节点 (i,~j),设 (a_i = ans_i - w_i,~a_j = ans_j - w_j) 且 (a_i > a_j)。
考虑先放 (i) 再放 (j) 需要准备的梅花朵数是 (max(ans_i, ans_j + w_i))(一式),同理先放 (j) 所需要准备的梅花朵数是 (max(ans_j, ans_i + w_j))(二式)。
由于 (a_i = ans_i - w_i),得 (ans_i = a_i + w_i)。(ans_j) 同理。对一式二式分别提出 (w)。
则
考虑一式的 (max) 如果取 (a_i),那么 ( ext{一式} = w_i + a_i < w_i + a_i + w_j = ext{二式})
如果取 (ans_j),那么 ( ext{一式} = w_i + w_j + a_j < w_i + w_j + w_i = ext{二式})
因此,一式恒小于二式,先放 (i) 更优。
据此做数学归纳可得,按照 (ans - w) 的不升序排序后的序列是最优的。
于是即可排序以后用上面的方式统计答案,时间复杂度 (O(n log n)),期望得分 (20~pts)
测试点 (15~sim 20):
发现上面的结论可以应用于这棵树上的任何一个节点,于是每个节点都按照这样的方法排序即可。时间复杂度 (O(n log n)),期望得分 (30 pts)。