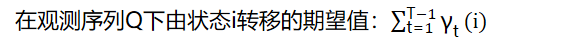【ML-13-3】隐马尔科夫模型HMM--Baum-Welch(鲍姆-韦尔奇)
【ML-13-4】隐马尔科夫模型HMM--预测问题Viterbi(维特比)算法
目录
- 基础--HMM常用概率的计算
- HMM模型参数求解概述
- Baum-Welch算法原理
- Baum-Welch算法推导
- Baum-Welch算法总结
一、基础--HMM常用概率计算
利用前向概率和后向概率,我们可以计算出HMM中单个状态和两个状态的概率公式。
1.1 单个状态的概率
求给定模型λ和观测序列Q的情况下,在时刻t处于状态si的概率,记做:

单个状态概率的意义主要是用于判断在每个时刻最可能存在的状态,从而可以得到一个状态序列作为最终的预测结果。
利用前向概率和后向概率的定义可知:
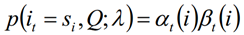
由上面两个表达式可知:
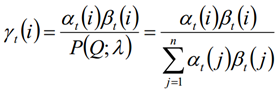
1.2 两个状态的联合概率
求给定模型λ和观测序列Q的情况下,在时刻t处于状态si并时刻t+1处于状态sj概率,记做:
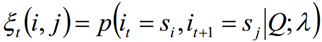
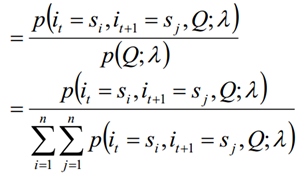
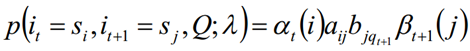
1.3 上述两种求和可以得到:
二、HMM模型参数求解概述
在本篇我们会讨论HMM模型参数求解的问题,即已知观测序列Q={q1,q2,...,qT},估计模型λ=(A,B,π)的参数,使得在该模型下观测序列P(Q|λ)最大。这个问题在HMM三个问题里算是最复杂的。在研究这个问题之前,建议先阅读这个系列的前两篇以熟悉HMM模型和HMM的前向后向算法,以及EM算法原理总结
HMM模型参数求解根据已知的条件可以分为两种情况。第一种情况较为简单,就是我们已知D个长度为T的观测序列和对应的隐藏状态序列,直接利用大数定理的结论"频率的极限是概率",直接给出HMM的参数估计;
1.1 假设所有样本中初始隐藏状态为qi的频率计数为S(i),那么初始概率分布为:
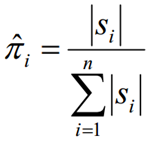
1.2 假设样本从隐藏状态qi转移到qj的频率计数是Sij,那么状态转移矩阵求得为:
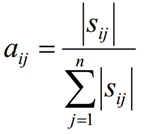
1.3 假设样本隐藏状态为qj且观测状态为vk的频率计数是qjk,那么观测状态概率矩阵为:
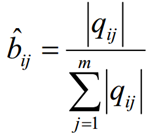
可见第一种情况下求解模型还是很简单的。但是在很多时候,我们无法得到HMM样本观察序列对应的隐藏序列,只有D个长度为T的观测序列,此时我们能不能求出合适的HMM模型参数呢?这就是我们的第二种情况,也是我们本文要讨论的重点。它的解法最常用的是鲍姆-韦尔奇算法(Baum-Welch),其实就是基于EM算法的求解,只不过Baum-Welch算法出现的时代,EM算法还没有被抽象出来,所以我们本文还是说鲍姆-韦尔奇算法法。这也提示我们抽象一种具体算法可能也是很重要的工程。
三、Baum-Welch算法原理


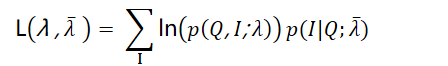
在M步,我们极大化上式,然后得到更新后的模型参数如下:
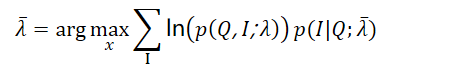

四、Baum-Welch算法推导
我们需要先计算联合分布P(Q,I;λ)的表达式如下:
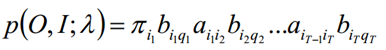
E步得到的期望表达式为:
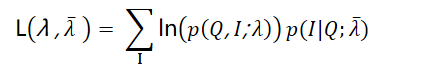
在M步要极大化上式:

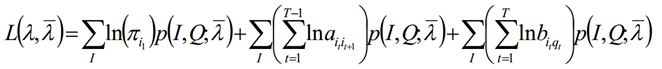
- 我们看看对模型参数Π的求导。由于Π只在上式中括号里的第一部分出现,因此我们对于Π的极大化式子为:
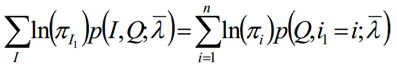
极大化上式,使用拉格朗日乘子法:
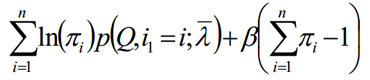
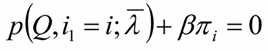
求和相加可得:

再代入可得到:
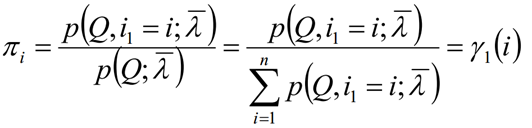
- 极大化L,使用拉格朗日乘子法,求解aij的值:
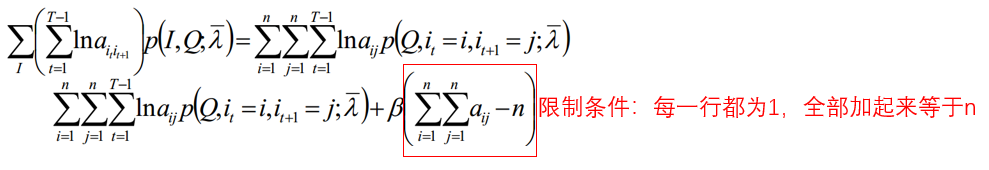
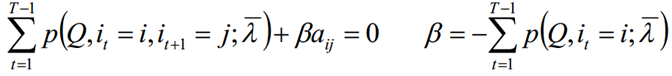
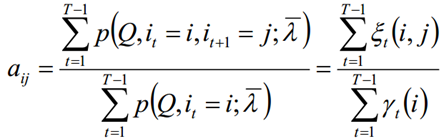
- 同理:极大化L,使用拉格朗日乘子法,求解bij的值
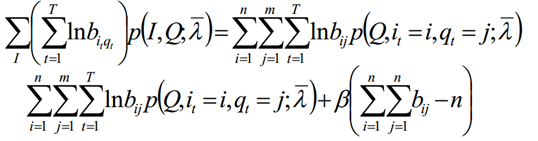
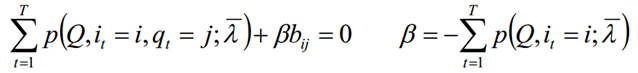
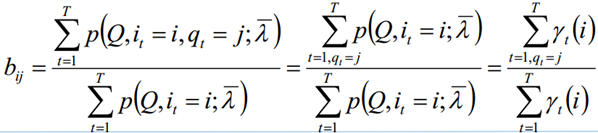
- 汇总:极大化L函数,分别可以求得π、a、b的值。

五、Baum-Welch算法总结
这里我们概括总结下鲍姆-韦尔奇算法的流程。
输入: D个观测序列样本
输出:HMM模型参数
具体流程:
1)随机初始化所有的πi,aij,bij
2) 对于每个样本d=1,2,...D,用前向后向算法计算γ,ξ
3) 更新模型参数:
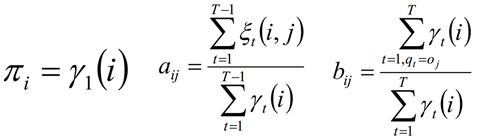
4) 如果πi,aij,bij的值已经收敛,则算法结束,否则回到第2)步继续迭代。
附件一:手写练习