剑指offer_49_丑数

丑数

题目链接：https://leetcode-cn.com/problems/chou-shu-lcof/

题目内容：

我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

示例:

输入: n = 10
输出: 12
解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

说明:

1. 1 是丑数。
2. n 不超过1690。

题目解析

题目解析内容来自于题解中 Krahets

做题首先得明白题意。对于此道题，我们首先要做的事儿，是取搞清楚这个丑数是个啥。

根据题意和相关资料得知，丑数 = 某小丑数 X 某因子

其中，因子只有 2， 3， 5 三个。示例： 10 = 5 X 2，则 10 即是丑数

设已知长度为 n 的丑数序列 x₁, x₂, .. , x_n, 求第 n + 1 个丑数 x_n+1。根据上面我们推出的性质，可知，这个 x_n+1 只可能下面三种情况之一得到的。（索引 a, b, c 是 1 ~ n-1 中的未知数）

x_n+1 = x_a X 2 , x_n+1 = x_b X 3 , x_n+1 = x_c X 5 ,

因为 x_n+1 是 最接近 X_n 的丑数，就好像丑数 10 的右边，是 2 * 6， 3 * 4 ，5*3 中最小的那个一样，因此

​ x_n+1 = min( x_a X 2 , x_b X 3 , x_c X 5 )

因此，我们可以设置 a， b， c 三个指针指向首个丑数(即 1)，循环根据递推公式得到下个丑数，并每轮将对应的指针 + 1 即可。

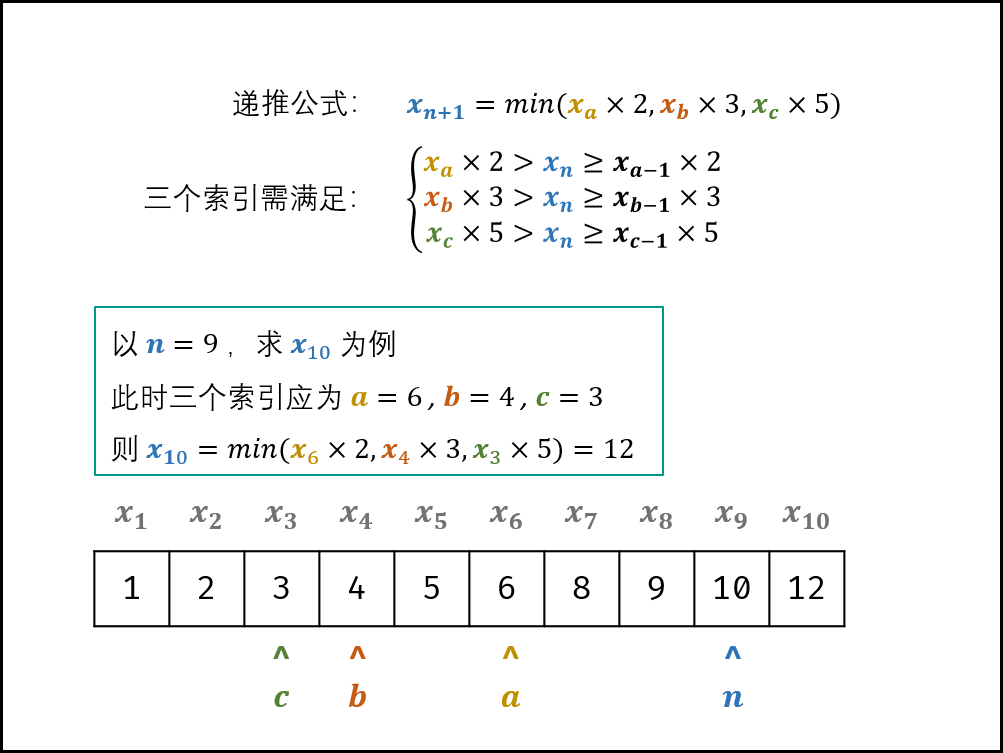
动态规划解析：

• 状态定义：设动态规划表为一维数组 dp，dp[i] 代表第 i + 1 个丑数

• 转移方程：

  1. 当索引 a， b， c满足下列条件时， dp[i] 为三种情况的最小值；
  2. 每轮计算 dp[i]后，需要更新 a，b，c 的值，使其始终满足方程条件。实现方法：分别独立判断 dp[i] 和 dp[a] * 2, dp[b] * 3, dp[c] * 5 的大小关系，若相等，则将对应的索引 a，b，c 加 1.

• 初始状态：dp[0] = 1, 即第一个丑数为 1；

• 返回值：dp[n - 1], 即返回第 n 个丑数

复杂度分析

• 时间复杂度O(N): 其中 N = n，动态规划需要遍历计算 dp 列表
• 空间复杂度O(N): 长度为 N 的 dp 列表使用 O(N) 的额外空间

代码

class Solution():
    def nthUglyNumber(self, n):
        dp, a, b, c = [1] * n, 0, 0, 0
        for i in range(1, n):
            n2, n3, n5 = dp[a] * 2, dp[b] * 3, dp[c] * 5
            dp[i] = min(n2, n3, n5)
            if dp[i] == n2:
                a += 1
            if dp[i] == n3:
                b += 1
            if dp[i] == n5:
                c += 1
        return dp[-1]
    
if __name__ == "__main__":
    solution = Solution()
    res = solution.nthUglyNumber(10)
    print(res)

本题需要动态规划知识。有不清楚逻辑的建议到题解评论中看一下sunrise的解释