数据结构杂谈（三）堆排序

堆

用数组存储一个堆，看成一个近似的完全二叉树。堆有自己的尺寸（不一定与数组长度相同）。

堆的性质：父结点比儿子结点大是最大堆；父节点比儿子节点小是最小堆。

本文以最大堆为例。

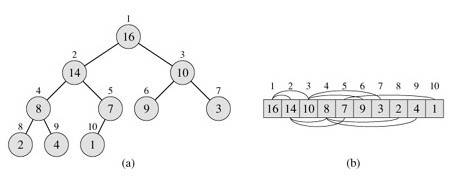
对于一个结点i，其父结点标号是i/2向下取整，左子结点是2*i，右子结点是2*i+1。

堆的高度是log(n)。

堆排序的思想

堆排序的本质是淘汰赛。分组比赛最终得到冠军。

一个典型的淘汰赛

要实现堆排序，需要以下步骤。

1. 对于不符合堆性质的地方，需要进行重建堆
2. 对于初始的情况，需要初始建堆
3. 用1和2实现堆排序堆排序

重建堆

对于不符合堆性质（最大堆：父结点比儿子结点大）的地方，需要进行重建堆。

重建堆的思想：

1. 找到当前结点i、左子结点、右子结点中的最大值
2. 将最大的结点交换到当前i的位置
3. 由于交换之后可能破坏子树，需要对交换的子节点递归调用重建堆算法
4. 如果没有发生交换，则为递归出口

c++实现

void restoreHeap(MyArray &arr, int curr, int size)
{
    int leftSon = curr * 2 + 1;//元素标号从0开始，这里再加1
    int rightSon = curr * 2 + 2;
    int maxLoc = curr;
    if (leftSon<size)
        maxLoc = (arr[maxLoc]>arr[leftSon]) ? maxLoc : leftSon;
    if (rightSon<size)
        maxLoc = (arr[maxLoc]>arr[rightSon]) ? maxLoc : rightSon;
    if (maxLoc != curr)
    {
        arr.swap(curr, maxLoc);
        restoreHeap(arr, maxLoc, size);
    }
}

算法分析

重建堆的时间复杂度是O(n)

初始建堆

进行排序时，数组元素顺序进入堆中，未保证堆的性质，需要对堆进行初始化。

初始建堆的思想

从最后一个内结点向前不断重建堆，自底向上的重建。

c++实现

void initHeap(MyArray &arr, int size)
{
    for (int i = size / 2; i >= 0; i--)
    {
        restoreHeap(arr, i, size);
    }
}

算法分析

初始建堆的时间复杂度是O(n)

堆排序

对一个最大堆，最大元素在根结点的位置，将根与堆的最后一个元素交换，并将堆的尺寸减1，然后重建堆，直到排好序。

c++实现

void heapSort(MyArray& arr)
{
    int size = arr.len();
    initHeap(arr, size);
    while (size>0)
    {
        arr.swap(size-1, 0);
        --size;
        restoreHeap(arr, 0, size);
    }
}

算法分析

堆排序的时间复杂度是O(nlgn)

*关于MyArray类，请移步至我的上一篇博客http://www.cnblogs.com/yatesxu/p/5369976.html