归并排序
package sort; import java.util.Arrays; /** * 归并排序 * 〈功能详细描述〉 * * @author 17090889 * @see [相关类/方法](可选) * @since [产品/模块版本] (可选) */ public class MergeSortTest { public static void main(String[] args) { int[] arr = {6, 19, 80, 4, 3, 60, 1, 38}; //在排序前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间 int[] temp = new int[arr.length]; sort(arr, 0, arr.length - 1, temp); System.out.println(Arrays.toString(arr)); // int[][] a = new int[2][]; } private static void sort(int[] arr, int left, int right, int[] temp) { if (left < right) { int mid = (left + right) / 2; //左边归并排序,使得左子序列有序 sort(arr, left, mid, temp); //右边归并排序,使得右子序列有序 sort(arr, mid + 1, right, temp); //将两个有序子数组合并操作 merge(arr, left, mid, right, temp); } } private static void merge(int[] arr, int left, int mid, int right, int[] temp) { //左序列指针 int i = left; //右序列指针 int j = mid + 1; //临时数组指针 int t = 0; while (i <= mid && j <= right) { // 两个子数组首下标数据比较,小的一方将数据放入临时数组中,下标加1并继续和右边子数组的原来的数据比较 if (arr[i] <= arr[j]) { temp[t++] = arr[i++]; } else { temp[t++] = arr[j++]; } } //将左边剩余元素填充进temp中,若右边下标走完,左边还有数据,则将剩余数据依次放入临时数组中 while (i <= mid) { temp[t++] = arr[i++]; } //将右序列剩余元素填充进temp中,若左边数据走完,右边还有数据,则将剩余数据依次放进临时数组中 while (j <= right) { temp[t++] = arr[j++]; } t = 0; //将temp中的元素全部拷贝到原数组中 while (left <= right) { arr[left++] = temp[t++]; } } }
快速排序
package sort; import java.util.Arrays; /** * 〈一句话功能简述〉 * 〈功能详细描述〉 * * @author 17090889 * @see [相关类/方法](可选) * @since [产品/模块版本] (可选) */ public class QuickSortTest { // 快速排序test private static void quickSort(int[] num, int left, int right) { int i = left; int j = right; if (i > j) { return; } int base = num[left]; while (i != j) { while (num[j] >= base && i < j) { j--; } while (num[i] <= base && i < j) { i++; } if (i < j) { // 交换位置 int t = num[i]; num[i] = num[j]; num[j] = t; } } // 替换基数 num[left] = num[i]; num[i] = base; quickSort(num, left, i - 1); quickSort(num, i + 1, right); } public static void main(String[] args) { int[] num = {6, 1, 2, 7, 9, 3, 4, 5, 10, 8}; // quickSort(num, 0, 9); quickSort2(num, 0, 9); System.out.println(Arrays.toString(num)); } /** * 经对快速排序算法的思想研究得知,需要知道待排序数组,数组中待排序的左右下标,使用递归算法,出口是左右下标相遇 */ private static void quickSort2(int[] a, int left, int right) { if (left >= right) { return; } int i = left; int j = right; // 基数取最左边的一个数 int base = a[left]; while (i != j) { // 进行排序,先从最右边开始探测,找到小于等于基数的数则停下来,或者两哨兵相遇 while (a[j] >= base && j > i) { j--; } // 另一哨兵从左边开始探测,找到大于等于基数的数则停下来,或者两哨兵相遇 while (a[i] <= base && i < j) { i++; } // 两哨兵还未相遇 if (i < j) { int temp = a[i]; a[i] = a[j]; a[j] = temp; } } // 两哨兵相遇 // 和基准数交换位置 a[left] = a[i]; a[i] = base; // 分别对基数左边的数组和右边的数组进行递归排序 quickSort2(a, left, i - 1); quickSort2(a, i + 1, right); } }
如果每次基准元素都选择第一个元素的话,那么对于逆序的数列,时间复杂度就退化成了O(n^2) ;那么如何选择基准元素呢?可以从待排序列表中随机选择一个元素
然后将选择的元素和列表第一个元素进行交换。
冒泡排序
package sort; import java.util.Arrays; /** * 〈一句话功能简述〉 * 〈功能详细描述〉 * * @author 17090889 * @see [相关类/方法](可选) * @since [产品/模块版本] (可选) */ public class BubbleSortTest { // 冒泡排序 private static void bubbleSort(int[] a) { int len = a.length; for (int i = 0; i < len; i++) { // 第一次冒泡排序后就把最大的元素放在了最后一位,第二次排序就排最后一位之前的数组就可以了,i代表已经排好序的元素的数量 for (int j = 0; j < len - i - 1; j++) { if (a[j] > a[j + 1]) { int temp = a[j + 1]; a[j + 1] = a[j]; a[j] = temp; } } } } public static void main(String[] args) { int[] num = {6, 1, 2, 7, 9, 3, 4, 5, 10, 8}; bubbleSort(num); System.out.println(Arrays.toString(num)); } }
冒泡排序的优化,定义一个 布尔值,如果在一次冒泡排序中,没有元素进行交换,则代表已经完成排序,break退出循环
// 冒泡排序的优化 private static void optBubbleSort(int[] a) { int len = a.length; for (int i = 0; i < len - 1; i++) { // 定义标记此轮排序是否有元素交换的布尔值,默认false boolean exchange = false; for (int j = 0; j < len - i - 1; j++) { if (a[j] > a[j + 1]) { int temp = a[j + 1]; a[j + 1] = a[j]; a[j] = temp; exchange = true; } } if (!exchange) { //此轮没有元素交换 break; } } }
插入排序
package sort; import java.util.Arrays; /** * 直接插入排序 * 〈功能详细描述〉 * * @author 17090889 * @see [相关类/方法](可选) * @since [产品/模块版本] (可选) */ public class InsertSortTest { public static void insertSort(int[] a) { // 从第二个元素开始排序,碰到大于要排序的数将其往后移动一位 int length = a.length; for (int i = 1; i < length; i++) { // 要排序的数 int insertNUm = a[i]; // 第一个要比较的数的下标,也就是已经排好序的元素 int j = i - 1; while (j >= 0 && a[j] > insertNUm) { a[j + 1] = a[j]; j--; } // 将要排序的数插入响应的位置 a[j + 1] = insertNUm; } } public static void main(String[] args) { int[] a = {6, 19, 80, 4, 3, 60, 1, 38}; insertSort(a); System.out.println(Arrays.toString(a)); } }
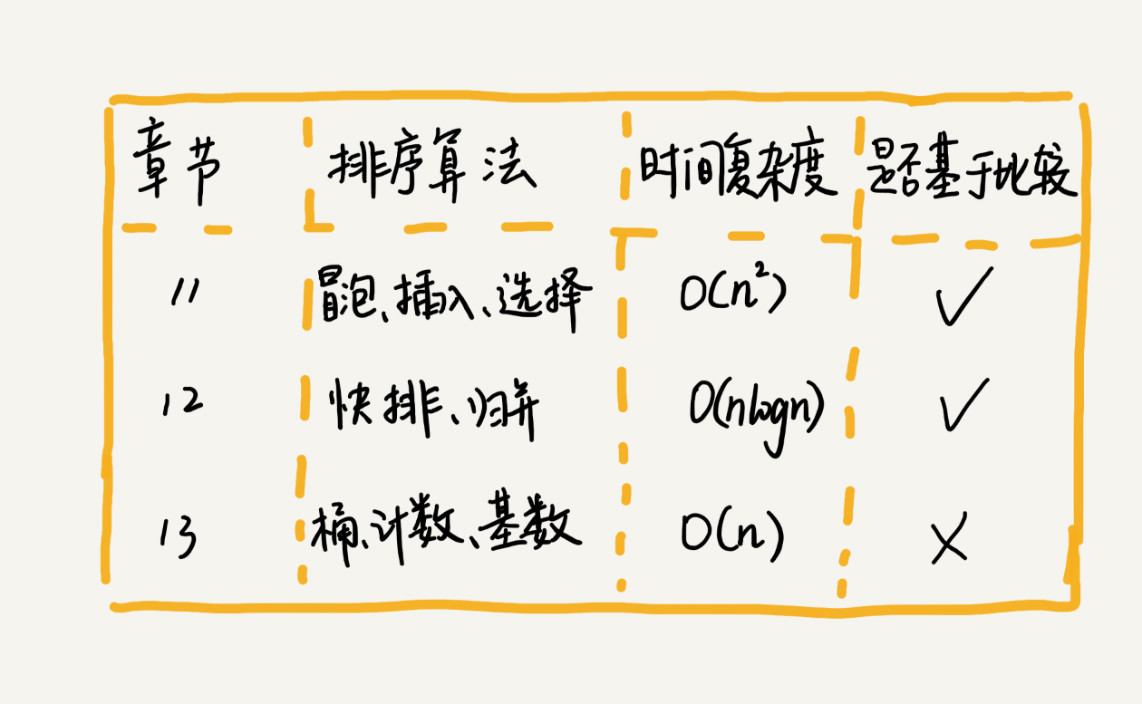
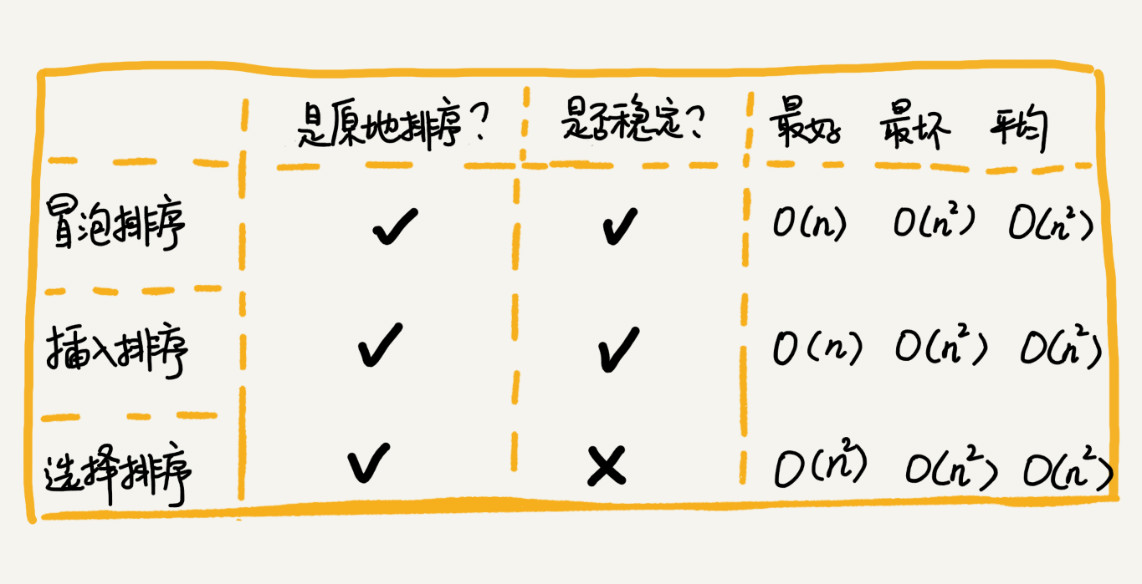
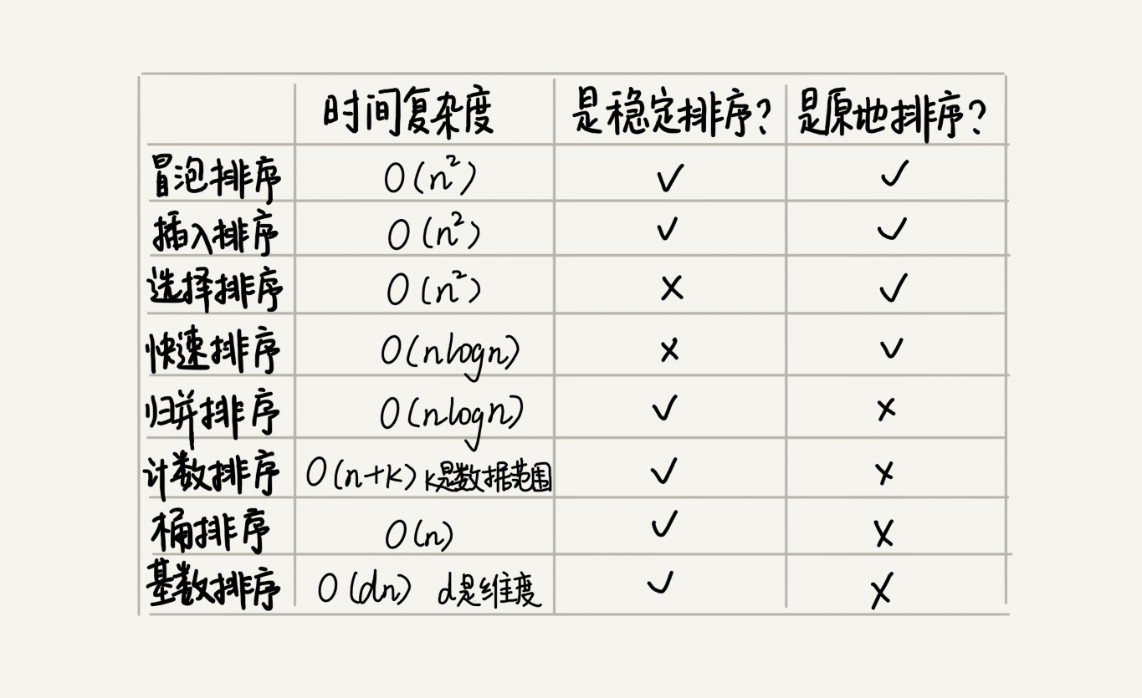
如何选择合适的排序算法:
二分查找(Binary Search)
也叫折半查找,是一种针对有序数据集合的查找算法。利用二分思想,每次都通过跟区间的中间元素的比较,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为0。
时间复杂度为O(logn)
假设数据大小是n,每次查找后数据都会缩小为原来的一半,也就是除以2。最后的情况下,直到查找区间被缩小为空,才停止。

可以看出这是一个等比数列,当查找停止时,n/2^k=1 时,k的值就是总共缩小的次数。而每一次缩小只涉及两个数据的大小比较,所以经过了
k次区间缩小操作,时间复杂度就是O(k)。通过n/2^k=1,得到k=logn,所以时间复杂度就是O(logn)。
O(logn) 这种对数时间复杂度。这是一种极其高效的时间复杂度,有的时候甚至比时间复杂度是常量级的O(1)的算法还要高效。因为,即便n非常大
,对应的logn也很小,比如n等于2的32次方,大约是42亿,也就是说如果在42亿个数据中用二分查找一个数据,最多需要比较32次。
堆排序
二叉堆是一个完全二叉树,其分为最大堆和最小堆
最大堆:最大堆的堆顶是整个堆中的最大元素,最大堆中的任何一个父节点的值,都大于或等于它左右孩子节点的值
最小堆:最小堆的堆顶是整个堆中的最小元素,最小堆中的任何一个父节点的值,都小于或等于它左右孩子节点的值
二叉堆的存储方式不是链式存储而是顺序存储,换句话说,二叉堆的所有节点都存储在数组中。假设父节点的下标是parent,那么它的左孩子的下标就是2xparent+1,
右孩子下标是2xparent+2.
/** * 堆排序,插入元素到最小堆中 * 〈功能详细描述〉 * * @author 17090889 * @see [相关类/方法](可选) * @since [产品/模块版本] (可选) */ public class HeapSort { /** * 插入元素到堆顶,然后进行堆顶元素的下沉 * * @param a * @param parentIndex */ public static void downAdjust(int[] a, int parentIndex) { int length = a.length; // 临时保存父节点的值,用于交换 int temp = a[parentIndex]; // 左子节点的索引 int childIndex = 2 * parentIndex + 1; while (childIndex < length) { // 如果有右子节点,则右子节点的下标 int rightChildIndex = childIndex + 1; // 判断是否有右子节点,如果有右子节点,则找到左右子节点中最小元素的下标 if (rightChildIndex < length && a[rightChildIndex] < a[childIndex]) { childIndex = rightChildIndex; } // 如果父节点小于任一子节点,则无需下沉,退出循环 if (a[parentIndex] < a[childIndex]) { break; } // 否则父子交换 a[parentIndex] = a[childIndex]; a[childIndex] = temp; // 进行下一次下沉循环的 parentIndex = childIndex; childIndex = childIndex * 2 + 1; } } /** * 给定乱序数组构建一个堆 * * @param a */ public static void buildHeap(int[] a) { // 从最后一个非叶子节点开始,依次做下沉调整,怎么找到最后一个非叶子结点呢?那就是有子节点的节点 // 即2*parentIndex+1=length-1,那么parentIndex=(length-1)/2 for (int i = (a.length - 1) / 2; i >= 0; i--) { downAdjust(a, i); } } public static void main(String[] args) { int[] a = {10, 7, 2, 6, 5, 3, 8, 9}; buildHeap(a); System.out.println(""); } }
线性排序:桶排序、计数排序、基数排序,这些排序的时间复杂度都是线性的,即O(n),之所以能做到线性的时间复杂度,主要原因是
这三个算法都是非基于比较的排序算法,都不涉及元素之间的比较排序。
桶排序
桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中。
核心思想是将要排序的数据按照数据区间分到几个有序的桶(每个桶可以数组实现,所有的桶用集合存储)中,每个桶里的数据再单独进行排序。
桶内排完序之后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。
计数排序
计数排序可以看成是桶排序的一种特殊情况,当要排序的n个数据,所处的范围并不大的时候,比如最大值是k,我们就可以把数据划分为k
个桶,每个桶内的数据值是相同的,省掉了桶内排序的时间。如20个随机整数,取值范围是0-10,要求以最快的速度把这20个整数从小到大进
行排序。由于取值范围是0-10这11个数,所以可以建立一个长度为11的数组,数组下标从0-10,元素的初始值全是0,然后遍历这个无序数列,
每一个整数按照其值找到索引对号入座,同时对应数组下标的元素进行加1操作。最后遍历完毕时,数组中下标存的值就是值为下标的数列的元素
出现的次数,然后遍历输出数组元素的下标值,元素的值为几,输出几次即可。
/** * 计数排序 * 〈功能详细描述〉 * * @author 17090889 * @see [相关类/方法](可选) * @since [产品/模块版本] (可选) */ public class CountSort { public static int[] countSort(int[] a) { int length = a.length; // 得到数列的最大值(考虑优化的话可以再得到最小值,然后使用最小值作为偏移量作为实际值和数组下标的对应关系) int max = a[0]; int min = a[0]; for (int i = 0; i < length; i++) { if (a[i] > max) { max = a[i]; } if (a[i] < min) { min = a[i]; } } // 得到计数数组的长度 int[] countArray = new int[max - min + 1]; // 遍历数列,填充统计数组 for (int i = 0; i < length; i++) { countArray[a[i] - min]++; } // 新数组 int[] newArr = new int[length]; int index = 0; // 遍历统计结果放到一个新的数组中 for (int i = 0; i < countArray.length; i++) { for (int j = 0; j < countArray[i]; j++) { newArr[index++] = i + min; } } return newArr; } public static void main(String[] args) { int[] a = new int[]{4, 4, 6, 5, 3, 2, 8, 1, 7, 5, 6, 7, 10}; int[] newArr = countSort(a); System.out.println(Arrays.toString(newArr)); } }
计数排序有它的局限性:
1、当数列最大和最小值差距过大时,并不适合用计数排序
2、当数列元素不是整数时,也不适合用计数排序