Q:每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0...m-1报数....这样下去....直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!^_^)。请你试着想下,哪个小朋友会得到这份礼品呢?(注:小朋友的编号是从0到n-1)
如果没有小朋友,请返回-1
T:(约瑟夫环问题)
1.使用单向循环链表(或者使用list,vector,queue都可以,whatever,方便就好):
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
int LastRemaining_Solution(int n, int m) {
if (n == 0 || m == 0)
return -1;
ListNode *head = new ListNode(0);
ListNode *list = head;
for (int i = 1; i < n; i++) {
ListNode *temp = new ListNode(i);
list->next = temp;
list = list->next;
}
list->next = head;
while (list->next != list) {
for (int i = 0; i < m - 1; i++)
list = list->next;
ListNode *temp2 = list->next;
list->next = temp2->next;
temp2->next = nullptr;
free(temp2);
}
return list->val;
}
2.约瑟夫环公式
因为数据是放在数组里,所以我在数组后面加上了数组的复制,以体现是环状的。我们先忽略图片里的箭头:
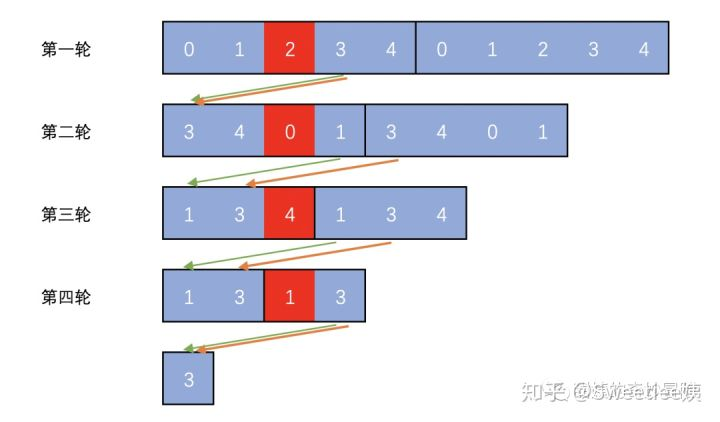
很明显我们每次删除的是第m个数字,我都标红了。
第一轮是 [0, 1, 2, 3, 4] ,所以是 [0, 1, 2, 3, 4] 这个数组的多个复制。这一轮 2 删除了。
第二轮开始时,从 3 开始,所以是 [3, 4, 0, 1] 这个数组的多个复制。这一轮 0 删除了。
第三轮开始时,从 1 开始,所以是 [1, 3, 4] 这个数组的多个复制。这一轮 4 删除了。
第四轮开始时,还是从 1 开始, 所以是 [1, 3] 这个数组的多个复制。这一轮 1 删除了。
最后剩下的数字是 3 。
图中的绿色的线指的是新的一轮的开头是怎么指定的,每次都是固定地向前移动m个位置。最后剩下的 3 的下标是 0 。
第四轮反推,补上m个位置,然后模上当时的数组大小 2, 位置是 (0 + 3 ) % 2 = 1 。
第三轮反推,补上m个位置,然后模上当时的数组大小 3, 位置是 (1 + 3) % 3 = 1 。
第二轮反推,补上m个位置,然后模上当时的数组大小 4, 位置是 (1 + 3) % 4 = 0 。
第一轮反推,补上m个位置,然后模上当时的数组大小 5, 位置是 (0 + 3) % 5 = 3 。
所以最终剩下的数字的下标就是 3 。因为数组是从0开始的,所以最终答案就是 3 。
总结一下反推的过程,就是 **(当前index + m) % 上一轮剩余数字的个数 **。
约瑟夫环问题的公式:(f(n,m) = (f(n-1, m) + m) mod n)
虽然不是在证明这个公式,但是通过这种方式,希望你能理解这个公式。
int LastRemaining_Solution(int n, int m)
{
if(n == 0)
return -1;
if(n == 1)
return 0;
else
return (LastRemaining_Solution(n - 1, m) + m) % n;
}