Codeforces Round #548 div2 C

一道快速幂,因为忘记处理时 +modp 而产生负数错误,在此记录

题目大意

给出一颗生成树,树边有红边与黑边两种.
定义一个好的长度为k的序列为 ([a_1,a_2,dots,a_k]) 其中相邻两个点可以不相邻,则经过一条最短路径走到. 从(a_1)走到(a_k)至少经过一条黑边. 其中允许(a_i=a_j) && (i!=j)

例子:

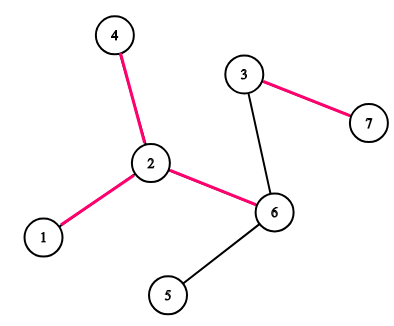
对于这颗树,考虑(k=3)时,([1,4,7],[5,5,3],[2,3,7])是好的,([1,4,6],[5,5,5],[3,7,3])是坏的
求好的序列的个数(mod 1e9+7)

思路

说实话我光理解题意加思路就想了不止半个小时

1. 计算总的序列数(f1=pow(n,k))
2. 计算坏的序列数(f2=sum{pow(i,k)})
3. (ans = f1-f2)

说了是不是没说? 但观察所给图像发现坏序列数确实更容易计算

我们把一个点只通过红边所能到达的点称为它的联通集,坏序列只会发生在在联通集内部移动的情况,所有(i=联通集的大小). 注意: 一个点不与红边相连时,它所在联通集为它本身. 一个联通集只计算一次

Code:

#include<bits/stdc++.h> 

#define ll long long 

#define inf 0x3f3f3f3f
using namespace std; 

const int maxn = 1*1e5+10;
const int modp = 1e9+7;
int n,k;

ll Pow(ll num,ll k){
	int res = 1;
	while(k){
		if(k%2==1)
			res = (res*num)%modp;
		num = (num*num)%modp;
		k>>=1;
	}
	return res;
}
vector<int> a[maxn];
int vis[maxn];

int dfs(int k){
	int res = 1;
	vis[k] = 1;
	for(int i=0;i<a[k].size();++i){
		if(vis[a[k][i]])	continue;
		vis[a[k][i]] = 1;
		res += dfs(a[k][i]);
	}
	return res;
}

int main(){
	cin >> n >> k;
	int f,t,p;
	for(int i=1;i<n;++i){
		scanf("%d %d %d",&f,&t,&p);
		if(p==0){
			a[f].push_back(t);
			a[t].push_back(f);
		}
	}
	ll res = Pow(n*1LL,k*1LL);
	
//	cout << res << endl;
	for(int i=1;i<=n;++i){
		if(vis[i])	continue;
		ll tmp = dfs(i);
//		cout << tmp << endl;
		res += modp-Pow(tmp*1LL,k*1LL);
		res %= modp;
	} 
	cout << res << endl;
	return 0;
} 

错误: res -=Pow(tmp1LL,k1LL);
直接减在模意义下会出现问题,(+mod)可以避免,计算完后在取一次模即可.