队列总结

　　队列简称队，是一种只允许在表的一端进行插入操作, 而在表的另一端进行删除操作的线性表。 允许插入的一端称为队尾， 队尾元素的位置由rear 指出； 允许删除的一端称为队头, 队头元素的位置由front指出。

　　

　　注：

　　1. 约定 rear指向队尾元素所指的位置

　　　front指向队头元素所在位置的前一个位置　

　

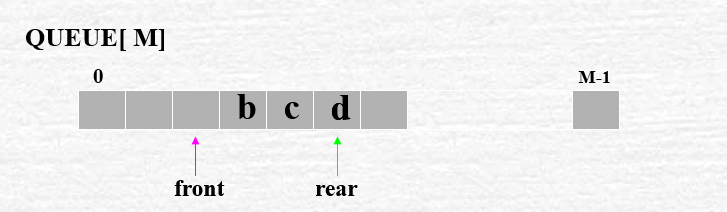
　　初始条件：front=-1  rear=-1     

　　测试为空：front==rear     //front所在位置相当于已经操作后的空位置，先移动后操作

　实现方式： 一、一维数组

　a）普通的一维数组队列存在假溢出的问题，即整体的front与rear向后靠，而前边元素实际空闲得不到利用--解决方法->b)

// test.cpp: 定义控制台应用程序的入口点。
#include "stdafx.h"
#include "stdlib.h"
#define M 1000
int queue[M];
int front = -1;
int rear = -1;
int add_queue(int yuansu)
{
    if (rear != M-1)
    {
        rear++;
        queue[rear] = yuansu;
        return 1;
    }
    else
    {
        printf("FULL");
        return 0;
    }
}
int out_queue()
{
    if (rear != front)
    {
        front++;
        return queue[front];
    }
    else
    {
        printf("EMPTY");
    }
}
int main()
{
    add_queue(1);
    add_queue(2);
    out_queue();
    out_queue();
    return 0;
}

 b） 循环队列

基本思想：

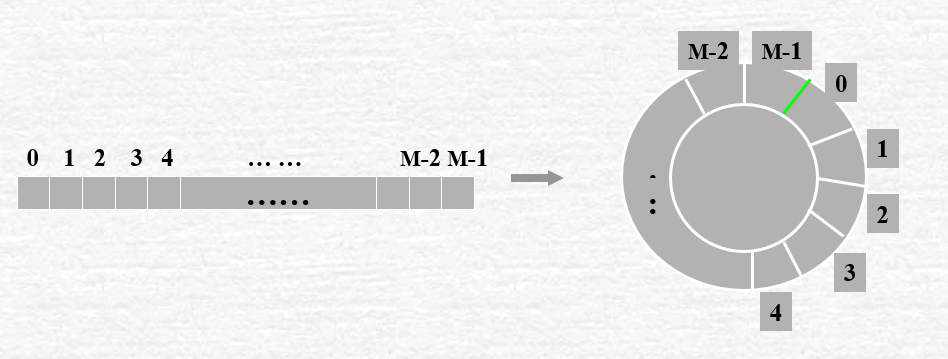
此处应注意循环队列与普通队列的不同点即可。

循环队列：

1. 初始rear=front=0； 

2.入队操作： rear=(rear+1)%M 

这句话相当于   if（rear<M-1)  rear++;

　　　　　　 else rear=0;

3.出队操作：front=（front+1）%M

应特别注意：循环队列牺牲一个存储空间（0元素）来区分队空和队满。

队空条件： front==rear

队满条件：(rear+1)%M==front  //取余相当于能跨过终点

// test.cpp: 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include "stdlib.h"
#define M 4
int queue[M];
int front = 0;
int rear = 0; 
int add_queue(int yuansu)
{
    if (front != (rear + 1) % M)
    { 
        rear = (rear + 1) % M; queue[rear] = yuansu;
        return 1;
    }
    else
    {
        printf("FULL");
        return 0;
    }
}
int out_queue()
{
    int ch;
    if (rear != front)
    {    
        front = (front + 1) % M;
        ch = queue[front];
        return ch;
    }
    else
    {
        printf("EMPTY");
        return 0;
    }
}
int main()
{
    add_queue(1);
    add_queue(2);
    out_queue();
    out_queue();
    return 0;
}

二、队列的链表实现

 队列的链式存储结构是用一个线性链表表示一个队列， 指针 front 与rear 分别指向队头 元素与队尾元素所在的链结点。

队空的标志： rear==NULL'

// test.cpp: 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include"stdlib.h"
#include"stack.h"
struct node { char data;
struct node * link;
};
struct node *rear;
struct node *front;
void add_queue(char ch)
{
    struct node * p = (struct node *)malloc(sizeof(struct node));
    p->data = ch;
    p->link = NULL;

    if (rear == NULL)
    {
        front=p;
        rear = front;
    }
    else
    {
        rear->link = p;
        rear = p;

    }
}
char del_queue()
{
    char chtemp;
    if (front == NULL)
    {
        printf("EMPTY");
        return 0;
    }
    else
    {
        chtemp=front->data;
        front = front->link;
        return chtemp;
    }
}
int main()
{
    add_queue('1');
    add_queue('2');
    del_queue();
    del_queue();
    del_queue();
    return 0;
}