1.实数的定义
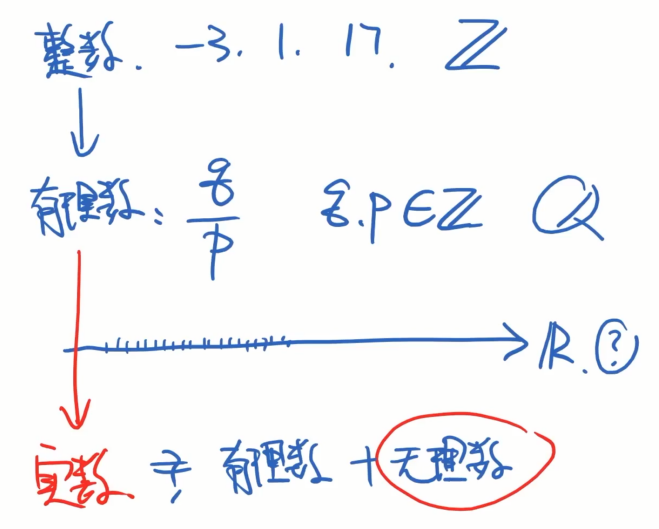
假设我们知道了整数的定义,像-3,1,17这些都属于整数Z。然后有理数则是两个整数相除q/p ,q,p属于Z,则是有理数Q。
什么是实数R呢?实数R代表横数轴上的所有数,如何定义实数呢?将实数定义为有理数+无理数?显然不可以,因为我们不知道还没有无理数的定义。
那要怎样定义实数呢?
戴德金 分划:
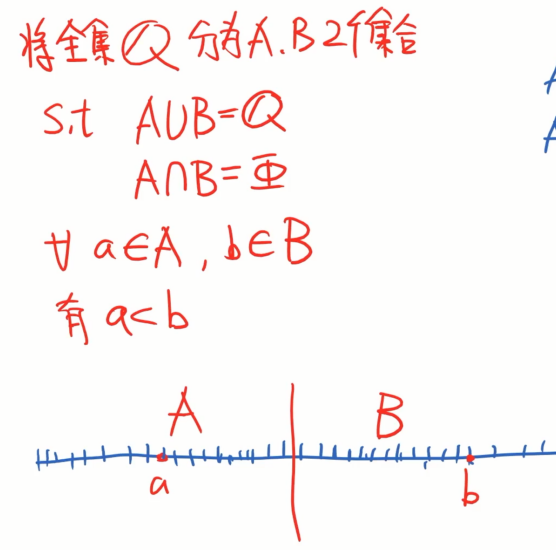
1.以有理数Q为全集,划分为A,B两个集合,使得 A∪B=Q,A∩B=∅,且只要a∈A,b∈B,则有a<b

2.则划分切割点的数有三种情况,如图所示,这些切割点的数的集合,就是实数。
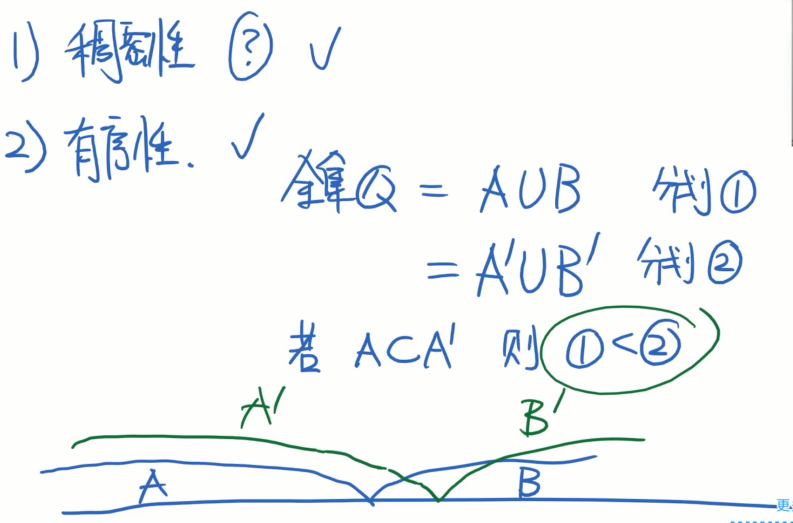
3.戴德金分划 的这种定义实数的方式,拥有稠密性(分无可分)和有序性(左小右大),符合数学对一个数集定义的要求。
单调有界序列存在极限(引理1)
2.实数元素的个数
1.整数、自然数、有理数,都是可列的,等势的,也就是元素的个数是相同的。
2.自然数少于实数(反证法)(有点绕额,感觉不是很重要的样纸)
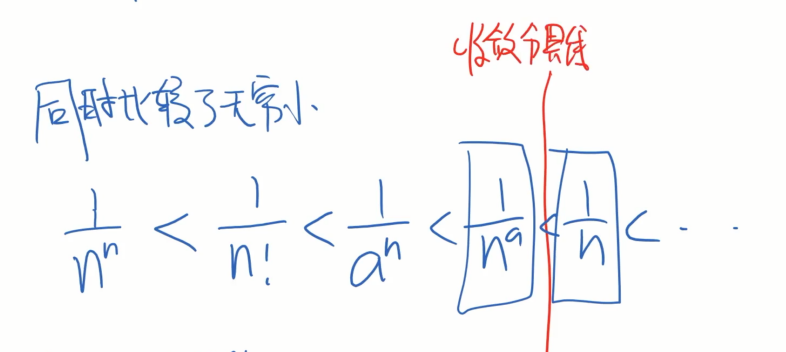
3.无穷大比较
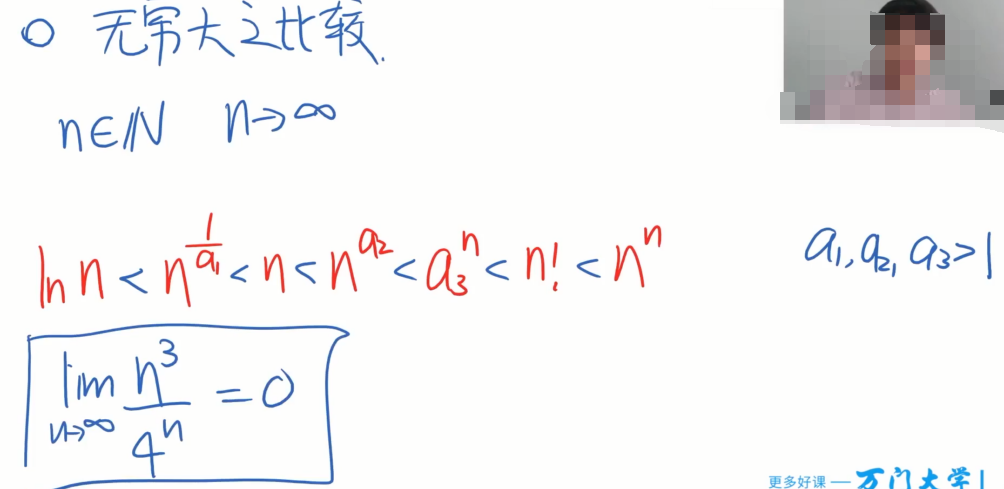
左边的函数除以右边的函数极限等于0
4.极限的定义

5.极限的四则运算
1.极限相加


6.极限的复合


7.连续性

连续的几个函数叠加,有可能会成为阶跃的函数
