讲在前面,本来想通过一个简单的多层感知机实验一下不同的优化方法的,结果写着写着就先研究起评价指标来了,之前也写过一篇:https://www.cnblogs.com/xiximayou/p/13700934.html
与上篇不同的是,这次我们新加了一些相关的实现,接下来我们慢慢来看。
利用pytorch搭建多层感知机分类的整个流程
导入相关包
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.utils.data import Dataset, DataLoader
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score, classification_report, confusion_matrix
from sklearn.preprocessing import label_binarize
from sklearn.metrics import roc_curve, auc
设置随机种子
设置随机种子总是需要的,它可以让我们的实验可以复现:即对于随机初始化的数据生成相同的结果。
np.random.seed(0)
torch.manual_seed(0)
torch.cuda.manual_seed_all(0)
加载数据
使用简单的sklearn自带的数字数据:
print("加载数据")
digits = load_digits()
data, label = digits.data, digits.target
# print(data.shape, label.shape)
train_data, test_data, train_label, test_label = train_test_split(data, label, test_size=.3, random_state=123)
print('训练数据:', train_data.shape)
print('测试数据:', test_data.shape)
定义相关参数
print("定义相关参数")
epochs = 30
batch_size = train_data.shape[0]
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
input_dim = data.shape[1]
hidden_dim = 256
output_dim = len(set(label))
构建数据集
pytorch构建数据集可以自己实现一个类,继承Dataset,然后在类中重写__len__和__getitem__方法。
print("构建数据集")
class DigitsDataset(Dataset):
def __init__(self, input_data, input_label):
data = []
for i,j in zip(input_data, input_label):
data.append((i,j))
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self, index):
d, l = self.data[index]
return d, l
在初始化的时候,我们将每一条数据及其标签放在一个列表中,然后在__len__中计算数据的总量,在__getitem__中根据索引取得每一条数据。接下我们我们要使用DataLoader将定义的数据集转换为数据加载器。
trainDataset = DigitsDataset(train_data, train_label)
testDataset = DigitsDataset(test_data, test_label)
# print(trainDataset[0])
# print(trainDataset[0])
trainDataLoader = DataLoader(trainDataset, batch_size=batch_size, shuffle=True, num_workers=2)
testDataLoader = DataLoader(testDataset, batch_size=batch_size, shuffle=False, num_workers=2)
定义模型
这里我们就简单的实现下多层感知机:
class Model(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(Model, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.relu = nn.ReLU()
self.fc2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
x = self.fc1(x)
x = self.relu(x)
x = self.fc2(x)
return x
定义损失函数、优化器和初始化相关参数
model = Model(input_dim, hidden_dim, output_dim)
print(model)
model.to(device)
print("定义损失函数、优化器")
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9, weight_decay=1e-4)
print("初始化相关参数")
for param in model.parameters():
nn.init.normal_(param, mean=0, std=0.01)
进行训练和测试
这里我们就仅仅使用sklearn自带的评价指标函数来计算评价指标:accuracy_score:计算准确率, precision_score:计算精确率, recall_score:计算召回率, f1_score:计算f1, classification_report:分类报告, confusion_matrix:混淆矩阵。具体是怎么使用的,我们可以直接看代码。
print("开始训练主循环")
total_step = len(trainDataLoader)
model.train()
for epoch in range(epochs):
tot_loss = 0.0
tot_acc = 0.0
train_preds = []
train_trues = []
# model.train()
for i,(train_data_batch, train_label_batch) in enumerate(trainDataLoader):
train_data_batch = train_data_batch.float().to(device) # 将double数据转换为float
train_label_batch = train_label_batch.to(device)
outputs = model(train_data_batch)
# _, preds = torch.max(outputs.data, 1)
loss = criterion(outputs, train_label_batch)
# print(loss)
#反向传播优化网络参数
loss.backward()
optimizer.step()
optimizer.zero_grad()
#累加每个step的损失
tot_loss += loss.data
train_outputs = outputs.argmax(dim=1)
train_preds.extend(train_outputs.detach().cpu().numpy())
train_trues.extend(train_label_batch.detach().cpu().numpy())
# tot_acc += (outputs.argmax(dim=1) == train_label_batch).sum().item()
sklearn_accuracy = accuracy_score(train_trues, train_preds)
sklearn_precision = precision_score(train_trues, train_preds, average='micro')
sklearn_recall = recall_score(train_trues, train_preds, average='micro')
sklearn_f1 = f1_score(train_trues, train_preds, average='micro')
print("[sklearn_metrics] Epoch:{} loss:{:.4f} accuracy:{:.4f} precision:{:.4f} recall:{:.4f} f1:{:.4f}".format(epoch, tot_loss, sklearn_accuracy, sklearn_precision, sklearn_recall, sklearn_f1))
test_preds = []
test_trues = []
model.eval()
with torch.no_grad():
for i,(test_data_batch, test_data_label) in enumerate(testDataLoader):
test_data_batch = test_data_batch.float().to(device) # 将double数据转换为float
test_data_label = test_data_label.to(device)
test_outputs = model(test_data_batch)
test_outputs = test_outputs.argmax(dim=1)
test_preds.extend(test_outputs.detach().cpu().numpy())
test_trues.extend(test_data_label.detach().cpu().numpy())
sklearn_precision = precision_score(test_trues, test_preds, average='micro')
sklearn_recall = recall_score(test_trues, test_preds, average='micro')
sklearn_f1 = f1_score(test_trues, test_preds, average='micro')
print(classification_report(test_trues, test_preds))
conf_matrix = get_confusion_matrix(test_trues, test_preds)
print(conf_matrix)
plot_confusion_matrix(conf_matrix)
print("[sklearn_metrics] accuracy:{:.4f} precision:{:.4f} recall:{:.4f} f1:{:.4f}".format(sklearn_accuracy, sklearn_precision, sklearn_recall, sklearn_f1))
定义和绘制混淆矩阵
额外的,我们补充一下混淆矩阵的计算和绘制。
def get_confusion_matrix(trues, preds):
labels = [0,1,2,3,4,5,6,7,8,9]
conf_matrix = confusion_matrix(trues, preds, labels)
return conf_matrix
def plot_confusion_matrix(conf_matrix):
plt.imshow(conf_matrix, cmap=plt.cm.Greens)
indices = range(conf_matrix.shape[0])
labels = [0,1,2,3,4,5,6,7,8,9]
plt.xticks(indices, labels)
plt.yticks(indices, labels)
plt.colorbar()
plt.xlabel('y_pred')
plt.ylabel('y_true')
# 显示数据
for first_index in range(conf_matrix.shape[0]):
for second_index in range(conf_matrix.shape[1]):
plt.text(first_index, second_index, conf_matrix[first_index, second_index])
plt.savefig('heatmap_confusion_matrix.jpg')
plt.show()
结果显示
加载数据
训练数据: (1257, 64)
测试数据: (540, 64)
定义相关参数
构建数据集
定义计算评价指标
定义模型
Model(
(fc1): Linear(in_features=64, out_features=256, bias=True)
(relu): ReLU()
(fc2): Linear(in_features=256, out_features=10, bias=True)
)
定义损失函数、优化器
初始化相关参数
开始训练主循环
[sklearn_metrics] Epoch:0 loss:2.2986 accuracy:0.1098 precision:0.1098 recall:0.1098 f1:0.1098
[sklearn_metrics] Epoch:1 loss:2.2865 accuracy:0.1225 precision:0.1225 recall:0.1225 f1:0.1225
[sklearn_metrics] Epoch:2 loss:2.2637 accuracy:0.1702 precision:0.1702 recall:0.1702 f1:0.1702
[sklearn_metrics] Epoch:3 loss:2.2316 accuracy:0.3174 precision:0.3174 recall:0.3174 f1:0.3174
[sklearn_metrics] Epoch:4 loss:2.1915 accuracy:0.5561 precision:0.5561 recall:0.5561 f1:0.5561
[sklearn_metrics] Epoch:5 loss:2.1438 accuracy:0.6881 precision:0.6881 recall:0.6881 f1:0.6881
[sklearn_metrics] Epoch:6 loss:2.0875 accuracy:0.7669 precision:0.7669 recall:0.7669 f1:0.7669
[sklearn_metrics] Epoch:7 loss:2.0213 accuracy:0.8226 precision:0.8226 recall:0.8226 f1:0.8226
[sklearn_metrics] Epoch:8 loss:1.9428 accuracy:0.8409 precision:0.8409 recall:0.8409 f1:0.8409
[sklearn_metrics] Epoch:9 loss:1.8494 accuracy:0.8552 precision:0.8552 recall:0.8552 f1:0.8552
[sklearn_metrics] Epoch:10 loss:1.7397 accuracy:0.8568 precision:0.8568 recall:0.8568 f1:0.8568
[sklearn_metrics] Epoch:11 loss:1.6140 accuracy:0.8632 precision:0.8632 recall:0.8632 f1:0.8632
[sklearn_metrics] Epoch:12 loss:1.4748 accuracy:0.8616 precision:0.8616 recall:0.8616 f1:0.8616
[sklearn_metrics] Epoch:13 loss:1.3259 accuracy:0.8640 precision:0.8640 recall:0.8640 f1:0.8640
[sklearn_metrics] Epoch:14 loss:1.1735 accuracy:0.8703 precision:0.8703 recall:0.8703 f1:0.8703
[sklearn_metrics] Epoch:15 loss:1.0245 accuracy:0.8791 precision:0.8791 recall:0.8791 f1:0.8791
[sklearn_metrics] Epoch:16 loss:0.8858 accuracy:0.8878 precision:0.8878 recall:0.8878 f1:0.8878
[sklearn_metrics] Epoch:17 loss:0.7625 accuracy:0.9006 precision:0.9006 recall:0.9006 f1:0.9006
[sklearn_metrics] Epoch:18 loss:0.6575 accuracy:0.9045 precision:0.9045 recall:0.9045 f1:0.9045
[sklearn_metrics] Epoch:19 loss:0.5709 accuracy:0.9077 precision:0.9077 recall:0.9077 f1:0.9077
[sklearn_metrics] Epoch:20 loss:0.5004 accuracy:0.9093 precision:0.9093 recall:0.9093 f1:0.9093
[sklearn_metrics] Epoch:21 loss:0.4436 accuracy:0.9101 precision:0.9101 recall:0.9101 f1:0.9101
[sklearn_metrics] Epoch:22 loss:0.3982 accuracy:0.9109 precision:0.9109 recall:0.9109 f1:0.9109
[sklearn_metrics] Epoch:23 loss:0.3615 accuracy:0.9149 precision:0.9149 recall:0.9149 f1:0.9149
[sklearn_metrics] Epoch:24 loss:0.3314 accuracy:0.9173 precision:0.9173 recall:0.9173 f1:0.9173
[sklearn_metrics] Epoch:25 loss:0.3065 accuracy:0.9196 precision:0.9196 recall:0.9196 f1:0.9196
[sklearn_metrics] Epoch:26 loss:0.2856 accuracy:0.9228 precision:0.9228 recall:0.9228 f1:0.9228
[sklearn_metrics] Epoch:27 loss:0.2673 accuracy:0.9236 precision:0.9236 recall:0.9236 f1:0.9236
[sklearn_metrics] Epoch:28 loss:0.2512 accuracy:0.9268 precision:0.9268 recall:0.9268 f1:0.9268
[sklearn_metrics] Epoch:29 loss:0.2370 accuracy:0.9300 precision:0.9300 recall:0.9300 f1:0.9300
precision recall f1-score support
0 0.98 0.98 0.98 59
1 0.86 0.86 0.86 56
2 0.98 0.91 0.94 53
3 0.98 0.93 0.96 46
4 0.95 0.97 0.96 61
5 0.98 0.91 0.95 57
6 0.96 0.96 0.96 57
7 0.92 0.98 0.95 50
8 0.87 0.81 0.84 48
9 0.77 0.91 0.83 53
accuracy 0.92 540
macro avg 0.93 0.92 0.92 540
weighted avg 0.93 0.92 0.92 540
[[58 0 0 0 1 0 0 0 0 0]
[ 0 48 0 0 0 0 1 0 0 7]
[ 0 2 48 0 0 0 0 1 2 0]
[ 0 0 1 43 0 0 0 1 1 0]
[ 0 0 0 0 59 0 0 1 1 0]
[ 0 0 0 0 1 52 0 0 0 4]
[ 1 1 0 0 0 0 55 0 0 0]
[ 0 0 0 0 0 0 0 49 0 1]
[ 0 4 0 0 1 1 1 0 39 2]
[ 0 1 0 1 0 0 0 1 2 48]]
<Figure size 640x480 with 2 Axes>
[sklearn_metrics] accuracy:0.9241 precision:0.9241 recall:0.9241 f1:0.9241
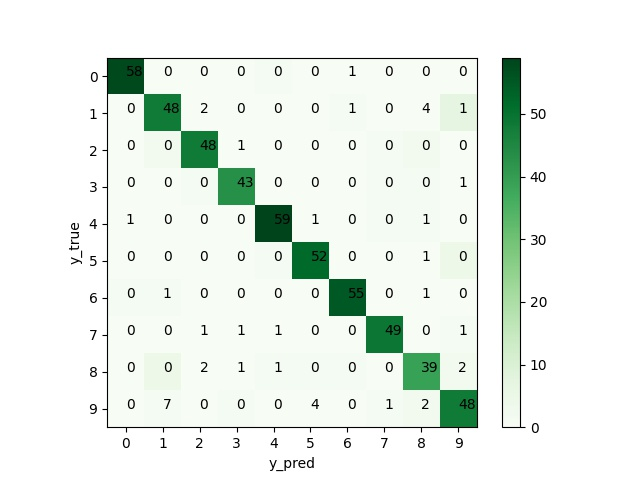
评价指标相关:准确率-精确率-召回率-f1
(1)基本知识
之前我们将pytorch加载数据、建立模型、训练和测试、使用sklearn评估模型都完整的过了一遍,接下来我们要再细讲下评价指标。首先大体的讲下四个基本的评价指标(针对于多分类):
accuracy:准确率。准确率就是有多少数据被正确识别了。针对整体,比如
预测标签[0,1,1,3,2,2,1],
真实标签[1,2,1,3,2,1,1],
此时正确率就是:5 / 7 = 0.7142,5是指列表中有5个对应的位置是相同的,即第0 2 3 4 6个位置,7是列表总长度。
precision:精确率,就是在预测为正的数据中,有多少是正确的。这里以标签为1的那一类说明,对于标签不为1的,我们先全部置为0(这里0表示的是负样本,不是第0类),则有:
预测标签[0,1,1,0,0,0,1]
真实标签[1,0,1,0,0,1,1]
在预测标签中,有3个预测为正,也就是1,在这三个中,有2个是与真实标签相同,也就是第2 6个位置,则精确率就是:2 / 3 = 0.6666
recall:在正样本中,有多少被正确识别。还是以标签为1的进行说明:在真实标签中有4个为1,在这4个中有2个被预测出来,所以召回率就是:2 / 4 =0.5000。
f1:综合考虑精确率和召回率。其值就是2 * p * r) / (p + r)
(2)具体计算
使用到的就是TP、FP、FN、TN,分别解释一下这些是什么:
第一位是True False的意思,第二位是Positive Negative。相当于第一位是对第二位的一个判断。
TP,即True Positive,预测为Positive的是True,也就是预测为正的,真实值是正。
FP,即False Positive,预测为Positive的是False,也就是预测为正的,真实值是负。
FN,即False Negative,预测为Negative的是False,也就是预测为负的,真实值是正。
TN,即True Negative,预测为Negative的是True,也就是预测为负的,真实值是是负。
那么根据之前我们的定义:
准确率(accuracy)不就是:(TP + FN) / (TP + FP + FN + TN)
精确率(precision)不就是:(TP) / (TP + FP)
召回率(recall)不就是:(TP) / (TP + FN)
f1 不就是:2 * precision * recall / (precision + recall)
(3)micro-f1和macro-f1
简单来讲,micro-f1就是先计算每一类的TP、FP、FN、TN,再计算相关的评价指标,在数据不平衡的情况下考虑到了每一类的数量。macro-f1就是先计算每一类的评价指标,最后取平均,它易受精确率和召回率较大的类的影响。
基本实现
接下来,我们要根据理解去实现评价指标。
(1)基本实现
def get_acc_p_r_f1(trues, preds):
labels = [0,1,2,3,4,5,6,7,8,9]
TP,FP,FN,TN = 0,0,0,0
for label in labels:
preds_tmp = np.array([1 if pred == label else 0 for pred in preds])
trues_tmp = np.array([1 if true == label else 0 for true in trues])
# print(preds_tmp, trues_tmp)
# print()
# TP预测为1真实为1
# TN预测为0真实为0
# FN预测为0真实为1
# FP预测为1真实为0
TP += ((preds_tmp == 1) & (trues_tmp == 1)).sum()
TN += ((preds_tmp == 0) & (trues_tmp == 0)).sum()
FN += ((preds_tmp == 0) & (trues_tmp == 1)).sum()
FP += ((preds_tmp == 1) & (trues_tmp == 0)).sum()
# print(TP, FP, FN)
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1 = 2 * precision * recall / (precision + recall)
return precision, recall, f1
def get_acc(trues, preds):
accuracy = (np.array(trues) == np.array(preds)).sum() / len(trues)
return accuracy
具体的就不细讲了,代码很容易看懂。
(2)根据混淆矩阵实现
def get_p_r_f1_from_conf_matrix(conf_matrix):
TP,FP,FN,TN = 0,0,0,0
labels = [0,1,2,3,4,5,6,7,8,9]
nums = len(labels)
for i in labels:
TP += conf_matrix[i, i]
FP += (conf_matrix[:i, i].sum() + conf_matrix[i+1:, i].sum())
FN += (conf_matrix[i, i+1:].sum() + conf_matrix[i, :i].sum())
print(TP, FP, FN)
precision = TP / (TP + FP)
recall = TP / (TP + FN)
f1 = 2 * precision * recall / (precision + recall)
return precision, recall, f1
def get_acc_from_conf_matrix(conf_matrix):
labels = [0,1,2,3,4,5,6,7,8,9]
return sum([conf_matrix[i, i] for i in range(len(labels))]) / np.sum(np.sum(conf_matrix, axis=0))
最终结果
加载数据
训练数据: (1257, 64)
测试数据: (540, 64)
定义相关参数
构建数据集
定义计算评价指标
定义模型
Model(
(fc1): Linear(in_features=64, out_features=256, bias=True)
(relu): ReLU()
(fc2): Linear(in_features=256, out_features=10, bias=True)
)
定义损失函数、优化器
初始化相关参数
开始训练主循环
[custom_metrics] Epoch:0 loss:2.2986 accuracy:0.1098 precision:0.1098 recall:0.1098 f1:0.1098
[sklearn_metrics] Epoch:0 loss:2.2986 accuracy:0.1098 precision:0.1098 recall:0.1098 f1:0.1098
[custom_metrics] Epoch:1 loss:2.2865 accuracy:0.1225 precision:0.1225 recall:0.1225 f1:0.1225
[sklearn_metrics] Epoch:1 loss:2.2865 accuracy:0.1225 precision:0.1225 recall:0.1225 f1:0.1225
[custom_metrics] Epoch:2 loss:2.2637 accuracy:0.1702 precision:0.1702 recall:0.1702 f1:0.1702
[sklearn_metrics] Epoch:2 loss:2.2637 accuracy:0.1702 precision:0.1702 recall:0.1702 f1:0.1702
[custom_metrics] Epoch:3 loss:2.2316 accuracy:0.3174 precision:0.3174 recall:0.3174 f1:0.3174
[sklearn_metrics] Epoch:3 loss:2.2316 accuracy:0.3174 precision:0.3174 recall:0.3174 f1:0.3174
[custom_metrics] Epoch:4 loss:2.1915 accuracy:0.5561 precision:0.5561 recall:0.5561 f1:0.5561
[sklearn_metrics] Epoch:4 loss:2.1915 accuracy:0.5561 precision:0.5561 recall:0.5561 f1:0.5561
[custom_metrics] Epoch:5 loss:2.1438 accuracy:0.6881 precision:0.6881 recall:0.6881 f1:0.6881
[sklearn_metrics] Epoch:5 loss:2.1438 accuracy:0.6881 precision:0.6881 recall:0.6881 f1:0.6881
[custom_metrics] Epoch:6 loss:2.0875 accuracy:0.7669 precision:0.7669 recall:0.7669 f1:0.7669
[sklearn_metrics] Epoch:6 loss:2.0875 accuracy:0.7669 precision:0.7669 recall:0.7669 f1:0.7669
[custom_metrics] Epoch:7 loss:2.0213 accuracy:0.8226 precision:0.8226 recall:0.8226 f1:0.8226
[sklearn_metrics] Epoch:7 loss:2.0213 accuracy:0.8226 precision:0.8226 recall:0.8226 f1:0.8226
[custom_metrics] Epoch:8 loss:1.9428 accuracy:0.8409 precision:0.8409 recall:0.8409 f1:0.8409
[sklearn_metrics] Epoch:8 loss:1.9428 accuracy:0.8409 precision:0.8409 recall:0.8409 f1:0.8409
[custom_metrics] Epoch:9 loss:1.8494 accuracy:0.8552 precision:0.8552 recall:0.8552 f1:0.8552
[sklearn_metrics] Epoch:9 loss:1.8494 accuracy:0.8552 precision:0.8552 recall:0.8552 f1:0.8552
[custom_metrics] Epoch:10 loss:1.7397 accuracy:0.8568 precision:0.8568 recall:0.8568 f1:0.8568
[sklearn_metrics] Epoch:10 loss:1.7397 accuracy:0.8568 precision:0.8568 recall:0.8568 f1:0.8568
[custom_metrics] Epoch:11 loss:1.6140 accuracy:0.8632 precision:0.8632 recall:0.8632 f1:0.8632
[sklearn_metrics] Epoch:11 loss:1.6140 accuracy:0.8632 precision:0.8632 recall:0.8632 f1:0.8632
[custom_metrics] Epoch:12 loss:1.4748 accuracy:0.8616 precision:0.8616 recall:0.8616 f1:0.8616
[sklearn_metrics] Epoch:12 loss:1.4748 accuracy:0.8616 precision:0.8616 recall:0.8616 f1:0.8616
[custom_metrics] Epoch:13 loss:1.3259 accuracy:0.8640 precision:0.8640 recall:0.8640 f1:0.8640
[sklearn_metrics] Epoch:13 loss:1.3259 accuracy:0.8640 precision:0.8640 recall:0.8640 f1:0.8640
[custom_metrics] Epoch:14 loss:1.1735 accuracy:0.8703 precision:0.8703 recall:0.8703 f1:0.8703
[sklearn_metrics] Epoch:14 loss:1.1735 accuracy:0.8703 precision:0.8703 recall:0.8703 f1:0.8703
[custom_metrics] Epoch:15 loss:1.0245 accuracy:0.8791 precision:0.8791 recall:0.8791 f1:0.8791
[sklearn_metrics] Epoch:15 loss:1.0245 accuracy:0.8791 precision:0.8791 recall:0.8791 f1:0.8791
[custom_metrics] Epoch:16 loss:0.8858 accuracy:0.8878 precision:0.8878 recall:0.8878 f1:0.8878
[sklearn_metrics] Epoch:16 loss:0.8858 accuracy:0.8878 precision:0.8878 recall:0.8878 f1:0.8878
[custom_metrics] Epoch:17 loss:0.7625 accuracy:0.9006 precision:0.9006 recall:0.9006 f1:0.9006
[sklearn_metrics] Epoch:17 loss:0.7625 accuracy:0.9006 precision:0.9006 recall:0.9006 f1:0.9006
[custom_metrics] Epoch:18 loss:0.6575 accuracy:0.9045 precision:0.9045 recall:0.9045 f1:0.9045
[sklearn_metrics] Epoch:18 loss:0.6575 accuracy:0.9045 precision:0.9045 recall:0.9045 f1:0.9045
[custom_metrics] Epoch:19 loss:0.5709 accuracy:0.9077 precision:0.9077 recall:0.9077 f1:0.9077
[sklearn_metrics] Epoch:19 loss:0.5709 accuracy:0.9077 precision:0.9077 recall:0.9077 f1:0.9077
[custom_metrics] Epoch:20 loss:0.5004 accuracy:0.9093 precision:0.9093 recall:0.9093 f1:0.9093
[sklearn_metrics] Epoch:20 loss:0.5004 accuracy:0.9093 precision:0.9093 recall:0.9093 f1:0.9093
[custom_metrics] Epoch:21 loss:0.4436 accuracy:0.9101 precision:0.9101 recall:0.9101 f1:0.9101
[sklearn_metrics] Epoch:21 loss:0.4436 accuracy:0.9101 precision:0.9101 recall:0.9101 f1:0.9101
[custom_metrics] Epoch:22 loss:0.3982 accuracy:0.9109 precision:0.9109 recall:0.9109 f1:0.9109
[sklearn_metrics] Epoch:22 loss:0.3982 accuracy:0.9109 precision:0.9109 recall:0.9109 f1:0.9109
[custom_metrics] Epoch:23 loss:0.3615 accuracy:0.9149 precision:0.9149 recall:0.9149 f1:0.9149
[sklearn_metrics] Epoch:23 loss:0.3615 accuracy:0.9149 precision:0.9149 recall:0.9149 f1:0.9149
[custom_metrics] Epoch:24 loss:0.3314 accuracy:0.9173 precision:0.9173 recall:0.9173 f1:0.9173
[sklearn_metrics] Epoch:24 loss:0.3314 accuracy:0.9173 precision:0.9173 recall:0.9173 f1:0.9173
[custom_metrics] Epoch:25 loss:0.3065 accuracy:0.9196 precision:0.9196 recall:0.9196 f1:0.9196
[sklearn_metrics] Epoch:25 loss:0.3065 accuracy:0.9196 precision:0.9196 recall:0.9196 f1:0.9196
[custom_metrics] Epoch:26 loss:0.2856 accuracy:0.9228 precision:0.9228 recall:0.9228 f1:0.9228
[sklearn_metrics] Epoch:26 loss:0.2856 accuracy:0.9228 precision:0.9228 recall:0.9228 f1:0.9228
[custom_metrics] Epoch:27 loss:0.2673 accuracy:0.9236 precision:0.9236 recall:0.9236 f1:0.9236
[sklearn_metrics] Epoch:27 loss:0.2673 accuracy:0.9236 precision:0.9236 recall:0.9236 f1:0.9236
[custom_metrics] Epoch:28 loss:0.2512 accuracy:0.9268 precision:0.9268 recall:0.9268 f1:0.9268
[sklearn_metrics] Epoch:28 loss:0.2512 accuracy:0.9268 precision:0.9268 recall:0.9268 f1:0.9268
[custom_metrics] Epoch:29 loss:0.2370 accuracy:0.9300 precision:0.9300 recall:0.9300 f1:0.9300
[sklearn_metrics] Epoch:29 loss:0.2370 accuracy:0.9300 precision:0.9300 recall:0.9300 f1:0.9300
precision recall f1-score support
0 0.98 0.98 0.98 59
1 0.86 0.86 0.86 56
2 0.98 0.91 0.94 53
3 0.98 0.93 0.96 46
4 0.95 0.97 0.96 61
5 0.98 0.91 0.95 57
6 0.96 0.96 0.96 57
7 0.92 0.98 0.95 50
8 0.87 0.81 0.84 48
9 0.77 0.91 0.83 53
accuracy 0.92 540
macro avg 0.93 0.92 0.92 540
weighted avg 0.93 0.92 0.92 540
[[58 0 0 0 1 0 0 0 0 0]
[ 0 48 0 0 0 0 1 0 0 7]
[ 0 2 48 0 0 0 0 1 2 0]
[ 0 0 1 43 0 0 0 1 1 0]
[ 0 0 0 0 59 0 0 1 1 0]
[ 0 0 0 0 1 52 0 0 0 4]
[ 1 1 0 0 0 0 55 0 0 0]
[ 0 0 0 0 0 0 0 49 0 1]
[ 0 4 0 0 1 1 1 0 39 2]
[ 0 1 0 1 0 0 0 1 2 48]]
<Figure size 640x480 with 2 Axes>
[custom_metrics] accuracy:0.9241 precision:0.9241 recall:0.9241 f1:0.9241
[sklearn_metrics] accuracy:0.9241 precision:0.9241 recall:0.9241 f1:0.9241
[cm_metrics] accuracy:0.9241 precision:0.9241 recall:0.9241 f1:0.9241
我们计算出的和sklearn自带的计算出的结果是一样的。为了确保是正确的,这里我们再打印一下测试的时候的每一类的精确率、召回率和micro-f1。
[custom_metrics] 0 precision:0.9831 recall:0.9831 f1:0.9831
[custom_metrics] 1 precision:0.8571 recall:0.8571 f1:0.8571
[custom_metrics] 2 precision:0.9796 recall:0.9057 f1:0.9412
[custom_metrics] 3 precision:0.9773 recall:0.9348 f1:0.9556
[custom_metrics] 4 precision:0.9516 recall:0.9672 f1:0.9593
[custom_metrics] 5 precision:0.9811 recall:0.9123 f1:0.9455
[custom_metrics] 6 precision:0.9649 recall:0.9649 f1:0.9649
[custom_metrics] 7 precision:0.9245 recall:0.9800 f1:0.9515
[custom_metrics] 8 precision:0.8667 recall:0.8125 f1:0.8387
[custom_metrics] 9 precision:0.7742 recall:0.9057 f1:0.8348
[cm_metrics] 0 precision:0.9831 recall:0.9831 f1:0.9831
[cm_metrics] 1 precision:0.8571 recall:0.8571 f1:0.8571
[cm_metrics] 2 precision:0.9796 recall:0.9057 f1:0.9412
[cm_metrics] 3 precision:0.9773 recall:0.9348 f1:0.9556
[cm_metrics] 4 precision:0.9516 recall:0.9672 f1:0.9593
[cm_metrics] 5 precision:0.9811 recall:0.9123 f1:0.9455
[cm_metrics] 6 precision:0.9649 recall:0.9649 f1:0.9649
[cm_metrics] 7 precision:0.9245 recall:0.9800 f1:0.9515
[cm_metrics] 8 precision:0.8667 recall:0.8125 f1:0.8387
[cm_metrics] 9 precision:0.7742 recall:0.9057 f1:0.8348
和sklearn中的classification_report是一致的。
绘制ROC和计算AUC
最后的最后,绘制ROC曲线和计算AUC,这两个评价指标就偷个懒,不介绍了,先要将标签进行二值化:
def get_roc_auc(trues, preds):
labels = [0,1,2,3,4,5,6,7,8,9]
nb_classes = len(labels)
fpr = dict()
tpr = dict()
roc_auc = dict()
print(trues, preds)
for i in range(nb_classes):
fpr[i], tpr[i], _ = roc_curve(trues[:, i], preds[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(trues.ravel(), preds.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(nb_classes)]))
# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(nb_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
# Finally average it and compute AUC
mean_tpr /= nb_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
# Plot all ROC curves
lw = 2
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],label='micro-average ROC curve (area = {0:0.2f})'.format(roc_auc["micro"]),color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],label='macro-average ROC curve (area = {0:0.2f})'.format(roc_auc["macro"]),color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(nb_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw, label='ROC curve of class {0} (area = {1:0.2f})'.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.savefig("ROC_10分类.png")
plt.show()
test_trues = label_binarize(test_trues, classes=[i for i in range(10)])
test_preds = label_binarize(test_preds, classes=[i for i in range(10)])
get_roc_auc(test_trues, test_preds)
