时间复杂度与空间复杂度

时间复杂度

时间复杂度是用来估计算法运行时间的一个单位

一般来说，时间复杂度高的比时间复杂度低的算法慢

常见的时间复杂度（按效率排序）

O(1)<O(logn)<O(n)<O(nlogn)<O(n²)<O(n²ologn)<O(n³)

空间复杂度

用来评估算法内内存占用大小的一个式子

冒泡排序

如这个列表
[9,5,1,3,8,4,6] 

列表中每两个相邻的数，如果前边的比后边的大，那么交换这两个数，依次循环能够拿到排序结果

def Bubble_sort(li):
    for i in range(len(li)-1):  # 外层循环：负责这个列表需要循环几趟  (len(li)-1:因为已经拿出一个数来进行比较，所以减一)
        for j in range(len(li)-1-i):  # 内层循环：每次这个列表内的两个数的比较  (len(li)-1-i:因为每走完一趟的时候，最后一个数是确定的，所以少排序一次)
            if li[j] > li[j+1]:  # li[j]为9，j+1第一次索引是0，li[j+1]为0+1等于1，所以条件成立
                li[j],li[j+1] = li[j+1],li[j]

选择排序

一趟遍历记录最小的数，放到第一个位置；

再一趟遍历记录剩余列表中最小的数，继续放置；

def select_sort(li):
    for i in range(len(li)):
        minLoc = i
        for j in range(i+1,len(li)):
            if li[j] < li[minLoc]:
                li[j],li[minLoc] = li[minLoc],li[j]

插入排序

列表被分为有序区和无序区两个部分。最初有序区只有一个元素。

每次从无序区选择一个元素，插入到有序区的位置，直到无序区变空。

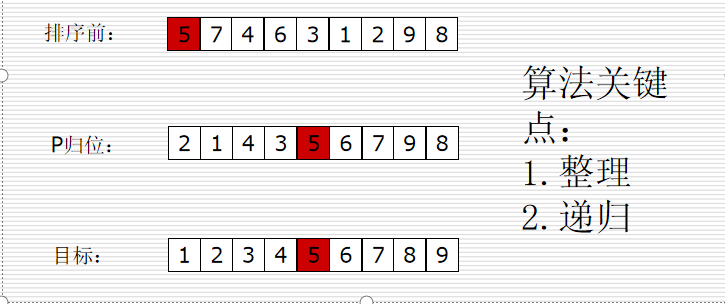
快速排序

快排思路： 取一个元素p（第一个元素），使元素p归位；

列表被p分成两部分，左边都比p小，右边都比p大； 递归完成排序。

def partition(li,left,right):
    tmp = li[left]
    while left < right:
        while left < right and li[right] >= tmp:
            right = right - 1
            li[left] = li[right]
        while left < right and li[right] >= tmp:
            left = left + 1
        li[right] = li[left]
    li[left] = tmp
    return left

def  quick_sort(li,left,right):
    if left < right:
        mid = partition(li,left,right)
        quick_sort(li,left,mid-1)
        quick_sort(li,mid+1,right)