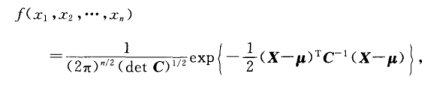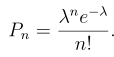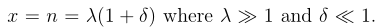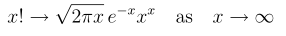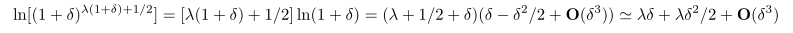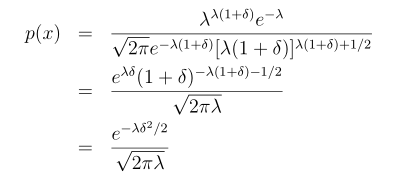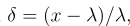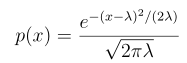作者：桂。
时间：2018-06-26 22:38:04
链接：https://www.cnblogs.com/xingshansi/p/9231644.html
前言
系统回顾数学知识，并学习补充相应的内容。随手记录在博客里，初步打算：
- 概率论与数理统计
- 高等数学
- 线性代数
- 矩阵论
- 数值优化
- 动态规划
- 运筹学
- 凸优化
- 随机过程
都是硬骨头，慢慢啃吧。
一、概率论与数理统计
浙江大学 第四版。
第一章
1- 确定性现象 / 不确定性现象。 —> 个别试验结果不确定，大量重复试验具有统计规律：随机现象。
2- 古典概型：又称等可能概型，特点：1）样本空间元素个数有限，2）每个基本时间等可能。
3- 排列、组合：
排列-permutation/Arrangement，故对应$A^m_n$，分为有放回、无放回。
组合-Combination，故对应$C^m_n$，分为有放回、无放回。
二者区别：排列需考虑元素之间的顺序，而组合不必考虑。
其实数独、拼图也都是组合，由此想到平时把各种信息罗列起来，有助于分析判断。
4- 条件概率：conditonal probability，P（A|B） = P(AB)/P(B)
对于互不相容的事件，P（U B_i | A） = ∑P(B_i A)/P(A)
一般地，P(B U C |A) = P(B|A)+P(C|A)-P(BC|A)，概率性质不受条件限制。
5- 乘法公式：
直观理解：先有老大，老大基础上再有老二，老大老二基础上再有老三，以此类推。
6- 全概率公式：
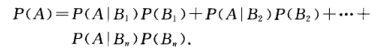
7- 贝叶斯公式：
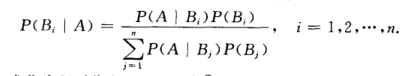
贝叶斯可以看作权重。
对比分析：
全概率： 因 -> 果；
贝叶斯： 果 -> 因；
贝叶斯应用的示例：
线索1：心情好 —— 按时吃饭概率为95%
线索2：心情不好——按时吃饭概率为50%
线索3：平时心情好的概率为90%
线索4：今早按时吃饭
推断：今天心情好的概率？
8- 独立性
P(AB)=P(A)P(B)，即概率上不受条件影响，自然相互独立。该定义与 互斥 不同。
第二章
1- 离散：分布率 + 概率 连续：分布函数 + 概率密度
2- 几种常见分布
这个需要梳理一下，
最基本的：0-1分布
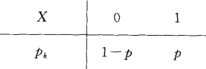
独立重复n次0-1试验，成为n重伯努利试验，发生k次的概率为组合问题：
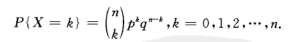，记为服从参数n,p的二项分布，也称伯努利分布。
当n->∞，【一段时间n等分，事件发生λ次】得：
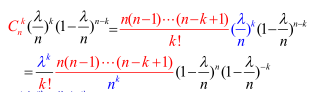
从而得到泊松分布：
泊松分布的均值方差都是λ，即np = np(1-p)，因此p -> 0 才行。
例如平时打游戏，一段时间内，怪物出现的个数是固定的，但怪物出现的时间是随机的，设定的时候怪物需要服从泊松分布。
更一般地，一段时间内平均发生λ次，该类模型都符合泊松分布。
容易证明：泊松分布相邻事件发生的间隔，符合指数分布。
泊松分布针对的是离散事件，事件n趋于无穷大，则时间间隔趋于无穷小，可认为是连续：
证明：
对于泊松分布：
假设：
这里用到斯特林公式【斯特林公式推导.pdf】:
借助斯特林公式（ Stirling’s formula）泊松分布的分布n!可表述为:
泊松分布进一步表述为：
由于：
泊松分布：
又因为
从而：
可不就是正态分布吗？
可以进一步推出：泊松分布的均值、方差都是λ，因此：泊松分布极限情况得出的正态分布：该正态分布均值、方差相等。
更多细节可参考：附件。
存疑：平时分析信号特性，通常假设噪声为高斯白噪声，即噪声统计特性符合正态分布，但采样信号已经是离散信号，假设服从泊松分布更合理？
概括：
0-1分布 —> 二项分布 —> 泊松分布【指数分布】 —> 正态分布【也可由中心极限定理推出】
正态分布是所有分布趋于极限大样本的分布，属于连续分布。二项分布与泊松分布，则都是离散分布，二项分布的极限分布是泊松分布、泊松分布的极限分布是正态分布，即np=λ，当n很大时，可以近似相等。当n很大时（还没达到连续的程度），可以用泊松分布近似代替二项分布；当n再变大，几乎可以看成连续时，二项分布和泊松分布都可以用正态分布来代替。
3- 复合函数的概率密度
证明：
对于h'(y)>0，F（Y<y） = F(g(X)<y) = F(X<h(y))
[F(X<h(y))]‘ = fx[h(y)]h'(y)，得证。其他情况类似。
第三章
二维联合概率分布，略。
第四章
1- 数学期望
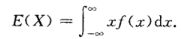
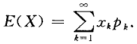
复合：
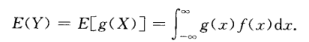
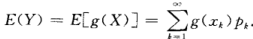
证明：
二维同理：
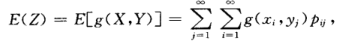
2- 方差
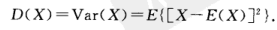
3- 切比雪夫（Chebyshev）不等式
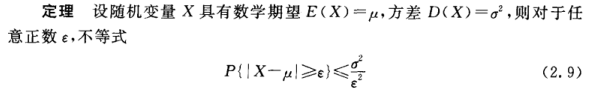
证明：
无需知道分布情况，只需知道一阶矩、二阶矩，借助切比雪夫估计概率P{|X-mu| >= epsilon} 的上界
4- 协方差与相关系数
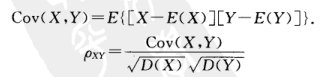
方差体现的是：数据围绕期望的波动情况。
协方差体现的是：
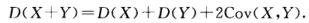
两个变量之和的方差与各自方差的差，也可从相关系数角度理解：表征了不同变量的相关性。
5- 混合矩
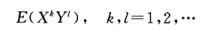
6- 中心矩
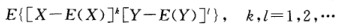
7- 协方差矩阵
8- 多维正态分布
