作者:桂。
时间:2017-08-22 12:30:33
链接:http://www.cnblogs.com/xingshansi/p/7411043.html
前言
记录经常用到的矩阵形式。
A-正交矩阵
定义:一实的正方矩阵Q∈Rnxn,称为正交矩阵,若:
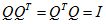
B-酉矩阵
定义:一实的正方矩阵U∈Cnxn,称为酉矩阵,若:
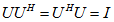
C-Vandermonde矩阵
定义:具有以下形式的mxn阶矩阵:

称为Vandermonde矩阵,其转置也是Vandermonde矩阵。
D-Toeplitz矩阵
定义:具有2n-1个元素的n阶矩阵
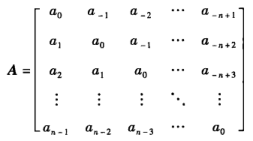
称为Toeplitz矩阵,简称T矩阵。
E-Hankel矩阵
定义:具有以下形式的n+1阶矩阵
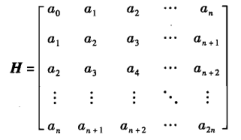
称为Hankel矩阵或正交对称矩阵(Orthosymmetric Matrix)。
F-Hadamard矩阵
定义:Hn∈Rnxn成为Hadamard矩阵,若它的所有元素取+1或者-1,且
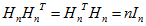
G-Hermitian矩阵
如果矩阵Anxn满足:
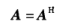
则称A为Hermitian矩阵。
H-符号矩阵(signature matrix)
一个对焦元素只取+1和-1两种值的NxN对角矩阵称为符号矩阵。
利用符号矩阵,可以引出J正交矩阵(也成为超正规矩阵):
定义:令J为NxN的符号矩阵,满足:
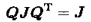
的NxN矩阵成为J正交矩阵(J-orthogonal matrix),可以理解为正交矩阵的广义形式,因为符号矩阵J全取1就是单位矩阵。或称超正规矩阵(Hepernormal matrix)。