“树”是一种重要的数据结构,本文浅谈二叉树的遍历问题,採用C语言描写叙述。
一、二叉树基础
1)定义:有且仅有一个根结点,除根节点外,每一个结点仅仅有一个父结点,最多含有两个子节点,子节点有左右之分。
2)存储结构
二叉树的存储结构能够採用顺序存储,也能够採用链式存储,当中链式存储更加灵活。
在链式存储结构中,与线性链表类似,二叉树的每一个结点採用结构体表示,结构体包括三个域:数据域、左指针、右指针。
二叉树在C语言中的定义例如以下:
struct BiTreeNode{
int c;
struct BiTreeNode *left;
struct BiTreeNode *right;
};
二、二叉树的遍历
“遍历”是二叉树各种操作的基础。二叉树是一种非线性结构,其遍历不像线性链表那样easy,无法通过简单的循环实现。
二叉树是一种树形结构,遍历就是要让树中的全部节点被且仅被訪问一次,即按一定规律排列成一个线性队列。二叉(子)树是一种递归定义的结构,包括三个部分:根结点(N)、左子树(L)、右子树(R)。依据这三个部分的訪问次序对二叉树的遍历进行分类,总共同拥有6种遍历方案:NLR、LNR、LRN、NRL、RNL和LNR。研究二叉树的遍历就是研究这6种详细的遍历方案,显然依据简单的对称性,左子树和右子树的遍历可互换,即NLR与NRL、LNR与RNL、LRN与RLN,分别相类似,因而仅仅需研究NLR、LNR和LRN三种就可以,分别称为“先序遍历”、“中序遍历”和“后序遍历”。
二叉树遍历通常借用“栈”这样的数据结构实现,有两种方式:递归方式及非递归方式。
在递归方式中,栈是由操作系统维护的,用户不必关心栈的细节操作,用户仅仅需关心“訪问顺序”就可以。因而,採用递归方式实现二叉树的遍历比較easy理解,算法简单,easy实现。
递归方式实现二叉树遍历的C语言代码例如以下:
//先序遍历--递归
int traverseBiTreePreOrder(BiTreeNode *ptree,int (*visit)(int))
{
if(ptree)
{
if(visit(ptree->c))
if(traverseBiTreePreOrder(ptree->left,visit))
if(traverseBiTreePreOrder(ptree->right,visit))
return 1; //正常返回
return 0; //错误返回
}else return 1; //正常返回
}
//中序遍历--递归
int traverseBiTreeInOrder(BiTreeNode *ptree,int (*visit)(int))
{
if(ptree)
{
if(traverseBiTreeInOrder(ptree->left,visit))
if(visit(ptree->c))
if(traverseBiTreeInOrder(ptree->right,visit))
return 1;
return 0;
}else return 1;
}
//后序遍历--递归
int traverseBiTreePostOrder(BiTreeNode *ptree,int (*visit)(int))
{
if(ptree)
{
if(traverseBiTreePostOrder(ptree->left,visit))
if(traverseBiTreePostOrder(ptree->right,visit))
if(visit(ptree->c))
return 1;
return 0;
}else return 1;
}
以上代码中,visit为一函数指针,用于传递二叉树中对结点的操作方式,其原型为:int (*visit)(char)。
大家知道,函数在调用时,会自己主动进行栈的push,调用返回时,则会自己主动进行栈的pop。函数递归调用无非是对一个栈进行返回的push与pop,既然递归方式能够实现二叉树的遍历,那么借用“栈”採用非递归方式,也能实现遍历。可是,这时的栈操作(push、pop等)是由用户进行的,因而实现起来会复杂一些,并且也不easy理解,但有助于我们对树结构的遍历有一个深刻、清晰的理解。
在讨论非递归遍历之前,我们先定义栈及各种须要用到的栈操作:
//栈的定义,栈的数据是“树结点的指针”
struct Stack{
BiTreeNode **top;
BiTreeNode **base;
int size;
};
#define STACK_INIT_SIZE 100
#define STACK_INC_SIZE 10
//初始化空栈,预分配存储空间
Stack* initStack()
{
Stack *qs=NULL;
qs=(Stack *)malloc(sizeof(Stack));
qs->base=(BiTreeNode **)calloc(STACK_INIT_SIZE,sizeof(BiTreeNode *));
qs->top=qs->base;
qs->size=STACK_INIT_SIZE;
return qs;
}
//取栈顶数据
BiTreeNode* getTop(Stack *qs)
{
BiTreeNode *ptree=NULL;
if(qs->top==qs->base)
return NULL;
ptree=*(qs->top-1);
return ptree;
}
//入栈操作
int push(Stack *qs,BiTreeNode *ptree)
{
if(qs->top-qs->base>=qs->size)
{
qs->base=(BiTreeNode **)realloc(qs->base,(qs->size+STACK_INC_SIZE)*sizeof(BiTreeNode *));
qs->top=qs->base+qs->size;
qs->size+=STACK_INC_SIZE;
}
*qs->top++=ptree;
return 1;
}
//出栈操作
BiTreeNode* pop(Stack *qs)
{
if(qs->top==qs->base)
return NULL;
return *--qs->top;
}
//推断栈是否为空
int isEmpty(Stack *qs)
{
return qs->top==qs->base;
}
首先考虑非递归先序遍历(NLR)。在遍历某一个二叉(子)树时,以一当前指针记录当前要处理的二叉(左子)树,以一个栈保存当前树之后处理的右子树。首先訪问当前树的根结点数据,接下来应该依次遍历其左子树和右子树,然而程序的控制流仅仅能处理其一,所以考虑将右子树的根保存在栈里面,当前指针则指向需先处理的左子树,为下次循环做准备;若当前指针指向的树为空,说明当前树为空树,不须要做不论什么处理,直接弹出栈顶的子树,为下次循环做准备。对应的C语言代码例如以下:
//先序遍历--非递归
int traverseBiTreePreOrder2(BiTreeNode *ptree,int (*visit)(int))
{
Stack *qs=NULL;
BiTreeNode *pt=NULL;
qs=initStack();
pt=ptree;
while(pt || !isEmpty(qs))
{
if(pt)
{
if(!visit(pt->c)) return 0; //错误返回
push(qs,pt->right);
pt=pt->left;
}
else pt=pop(qs);
}
return 1; //正常返回
}
相对于非递归先序遍历,非递归的中序/后序遍历稍复杂一点。
对于非递归中序遍历,若当前树不为空树,则訪问其根结点之前应先訪问其左子树,因而先将当前根节点入栈,然后考虑其左子树,不断将非空的根节点入栈,直到左子树为一空树;当左子树为空时,不须要做不论什么处理,弹出并訪问栈顶结点,然后指向其右子树,为下次循环做准备。
//中序遍历--非递归
int traverseBiTreeInOrder2(BiTreeNode *ptree,int (*visit)(int))
{
Stack *qs=NULL;
BiTreeNode *pt=NULL;
qs=initStack();
pt=ptree;
while(pt || !isEmpty(qs))
{
if(pt)
{
push(qs,pt);
pt=pt->left;
}
else
{
pt=pop(qs);
if(!visit(pt->c)) return 0;
pt=pt->right;
}
}
return 1;
}
//中序遍历--非递归--还有一种实现方式
int traverseBiTreeInOrder3(BiTreeNode *ptree,int (*visit)(int))
{
Stack *qs=NULL;
BiTreeNode *pt=NULL;
qs=initStack();
push(qs,ptree);
while(!isEmpty(qs))
{
while(pt=getTop(qs)) push(qs,pt->left);
pt=pop(qs);
if(!isEmpty(qs))
{
pt=pop(qs);
if(!visit(pt->c)) return 0;
push(qs,pt->right);
}
}
return 1;
}
最后谈谈非递归后序遍历。因为在訪问当前树的根结点时,应先訪问其左、右子树,因而先将根结点入栈,接着将右子树也入栈,然后考虑左子树,反复这一过程直到某一左子树为空;假设当前考虑的子树为空,若栈顶不为空,说明第二栈顶相应的树的右子树未处理,则弹出栈顶,下次循环处理,并将一空指针入栈以表示其还有一子树已做处理;若栈顶也为空树,说明第二栈顶相应的树的左右子树或者为空,或者均已做处理,直接訪问第二栈顶的结点,訪问完结点后,若栈仍为非空,说明整棵树尚未遍历完,则弹出栈顶,并入栈一空指针表示第二栈顶的子树之中的一个已被处理。
//后序遍历--非递归
int traverseBiTreePostOrder2(BiTreeNode *ptree,int (*visit)(int))
{
Stack *qs=NULL;
BiTreeNode *pt=NULL;
qs=initStack();
pt=ptree;
while(1) //循环条件恒“真”
{
if(pt)
{
push(qs,pt);
push(qs,pt->right);
pt=pt->left;
}
else if(!pt)
{
pt=pop(qs);
if(!pt)
{
pt=pop(qs);
if(!visit(pt->c)) return 0;
if(isEmpty(qs)) return 1;
pt=pop(qs);
}
push(qs,NULL);
}
}
return 1;
}
三、二叉树的创建
谈完二叉树的遍历之后,再来谈谈二叉树的创建,这里所说的创建是指从控制台依次(先/中/后序)输入二叉树的各个结点元素(此处为字符),用“空格”表示空树。
因为控制台输入是保存在输入缓冲区内,因此遍历的“顺序”就反映在读取输入字符的次序上。
下面是递归方式实现的先序创建二叉树的C代码。
//创建二叉树--先序输入--递归
BiTreeNode* createBiTreePreOrder()
{
BiTreeNode *ptree=NULL;
char ch;
ch=getchar();
if(ch==' ')
ptree=NULL;
else
{
ptree=(struct BiTreeNode *)malloc(sizeof(BiTreeNode));
ptree->c=ch;
ptree->left=createBiTreePreOrder();
ptree->right=createBiTreePreOrder();
}
return ptree;
}
对于空树,函数直接返回就可以;对于非空树,先读取字符并赋值给当前根结点,然后创建左子树,最后创建右子树。因此,要先知道当前要创建的树是否为空,才干做对应处理,“先序”遍历方式非常好地符合了这一点。可是中序或后序就不一样了,更重要的是,中序或后序方式输入的字符序列无法唯一确定一个二叉树。我还没有找到中序/后序实现二叉树的创建(控制台输入)的类似简单的方法,希望各位同仁网友指教哈!
四、执行及结果
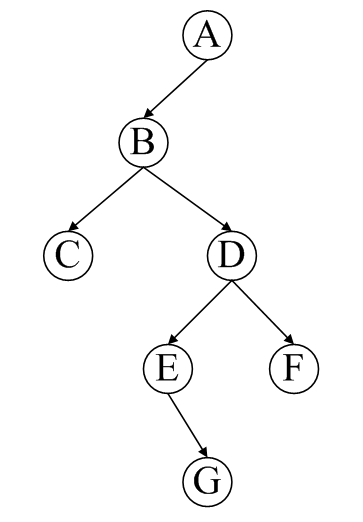
採用例如以下的二叉树进行測试,首先先序输入创建二叉树,然后依次调用各个遍历函数。
先序输入的格式:ABC ^ ^ D E ^ G ^ ^ F ^ ^ ^ (当中, ^ 表示空格字符)
遍历操作採用标准I/O库中的putchar函数,其原型为:int putchar(int);
各种形式遍历输出的结果为:
先序:ABCDEGF
中序:CBEGDFA
后序:CGEFDBA
測试程序的主函数例如以下:
int main(int argc, char* argv[])
{
BiTreeNode *proot=NULL;
printf("InOrder input chars to create a BiTree: ");
proot=createBiTreePreOrder(); //输入(ABC DE G F )
printf("PreOrder Output the BiTree recursively: ");
traverseBiTreePreOrder(proot,putchar);
printf("
");
printf("PreOrder Output the BiTree non-recursively: ");
traverseBiTreePreOrder2(proot,putchar);
printf("
");
printf("InOrder Output the BiTree recursively: ");
traverseBiTreeInOrder(proot,putchar);
printf("
");
printf("InOrder Output the BiTree non-recursively(1): ");
traverseBiTreeInOrder2(proot,putchar);
printf("
");
printf("InOrder Output the BiTree non-recursively(2): ");
traverseBiTreeInOrder3(proot,putchar);
printf("
");
printf("PostOrder Output the BiTree non-recursively: ");
traverseBiTreePostOrder(proot,putchar);
printf("
");
printf("PostOrder Output the BiTree recursively: ");
traverseBiTreePostOrder2(proot,putchar);
printf("
");
return 0;
}