AtCoder Grand Contest 015（C

花样式过DFS题

Problem Statement

Nuske has a grid with N rows and M columns of squares. The rows are numbered 1 through N from top to bottom, and the columns are numbered 1 through M from left to right. Each square in the grid is painted in either blue or white. If S_i,j is 1, the square at the i-th row and j-th column is blue; if S_i,j is 0, the square is white. For every pair of two blue square a and b, there is at most one path that starts from a, repeatedly proceeds to an adjacent (side by side) blue square and finally reaches b, without traversing the same square more than once.

Phantom Thnook, Nuske's eternal rival, gives Q queries to Nuske. The i-th query consists of four integers x_i,1, y_i,1, x_i,2 and y_i,2 and asks him the following: when the rectangular region of the grid bounded by (and including) the x_i,1-th row, x_i,2-th row, y_i,1-th column and y_i,2-th column is cut out, how many connected components consisting of blue squares there are in the region?

Process all the queries.

Constraints

• 1≤N,M≤2000
• 1≤Q≤200000
• S_i,j is either 0 or 1.
• S_i,j satisfies the condition explained in the statement.
• 1≤x_i,1≤x_i,2≤N(1≤i≤Q)
• 1≤y_i,1≤y_i,2≤M(1≤i≤Q)

---

Input

The input is given from Standard Input in the following format:

N M Q
S1,1..S1,M
:
SN,1..SN,M
x1,1 yi,1 xi,2 yi,2
:
xQ,1 yQ,1 xQ,2 yQ,2

Output

For each query, print the number of the connected components consisting of blue squares in the region.

---

Sample Input 1

Copy

3 4 4
1101
0110
1101
1 1 3 4
1 1 3 1
2 2 3 4
1 2 2 4

Sample Output 1

Copy

3
2
2
2

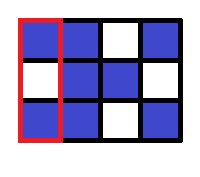
In the first query, the whole grid is specified. There are three components consisting of blue squares, and thus 3 should be printed.

In the second query, the region within the red frame is specified. There are two components consisting of blue squares, and thus 2 should be printed. Note that squares that belong to the same component in the original grid may belong to different components.

题意是求：（x1,y1）到(x2,y2)有多少个连成的块，由于数据过大，直接DFS肯定会超时，在网上看到一种解法好6，就是求出（x1，y1）到（x2，y2）之间的点，行边，列边。边是由两个正方形组成的。把点减去边数就是答案了。

#include <bits/stdc++.h>
using namespace std;
const int N = 2e3+10;
char a[N][N];
int vectex[N][N], edgeH[N][N], edgeW[N][N];

int main(){
    int n, m, q;
    scanf("%d %d %d
",&n,&m,&q);
    for(int i = 0; i < n; i ++){
        scanf("%s",a[i]);
    }
    for(int i = 0; i < n; i ++){
        for(int j = 0; j < m; j ++){
            vectex[i+1][j+1] = (a[i][j] == '1') + vectex[i+1][j] + vectex[i][j+1] -vectex[i][j];
            edgeH[i+1][j+1] = (a[i+1][j] == '1' && a[i][j] == '1') + edgeH[i+1][j] + edgeH[i][j+1] - edgeH[i][j];
            edgeW[i+1][j+1] = (a[i][j+1] == '1' && a[i][j] == '1') + edgeW[i+1][j] + edgeW[i][j+1] - edgeW[i][j];
        }
    }
    while(q--){
        int x1, x2, y1, y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        x1--;y1--;
        int vec = vectex[x2][y2] - vectex[x2][y1] - vectex[x1][y2] + vectex[x1][y1];
        int edg = edgeH[x2-1][y2] - edgeH[x2-1][y1] - edgeH[x1][y2] + edgeH[x1][y1] +
                    edgeW[x2][y2-1] - edgeW[x2][y1] - edgeW[x1][y2-1] + edgeW[x1][y1];
        printf("%d
",vec - edg);
    }
    return 0;
}