同余方程组:
先来看一道题目:有物不知其数,三三数之剩二;五五数之剩三;七七数之剩二。问物几何? 然后我们可以做如下变换,设x为所求的数。
x%3=2 x ≡ a1(%m1) ①
x%5=3 ===> x ≡ a2(%m2) ②
x%7=2 x ≡ a3(%m3)
根据前面两式可以得到
x = a1+m1y1 (1)
x = a2+m2y2
两式相减得到 m1y1 - m2y2 = a2 - a1 这是一个线性不定方程,可解出y1 ---> linearEquation(m1,-m2,a2-a1) 带回(1),得特解x0 = a1+m1*y1 --> 得到通解表达式 x =x0 + k*lcm(m1,m2) 得一个新方程 x = x0 (mod lcm(m1,m2))
代码:
/** * * @param a 余数组成的数组 * @param m 模组成的数组 * @return * @throws Exception */ public static long linearEquationGroup(Long[] a, Long[] m) throws Exception { int len = a.length; if (len == 0 && a[0] == 0) return m[0]; for (int i = 1; i < len; i++) { // 这里往前看是两个方程 long a2_a1 = a[i] - a[i - 1]; long d = linearEquation(m[i - 1], -m[i], a2_a1); // 现在的x是y1,用y1求得一个特解 long x0 = a[i - 1] + m[i - 1] * x; long lcm = m[i - 1] * m[i] / d; a[i] = (x0 % lcm + lcm) % lcm;// x0变成正数 m[i] = lcm; } // 合并完之后,只有一个方程 : x = a[len-1] (% m[len-1]) //long d = linearEquation(1, m[len-1], a[len-1]); return a[len - 1] % m[len - 1]; }
题目:POJ1006 生理周期

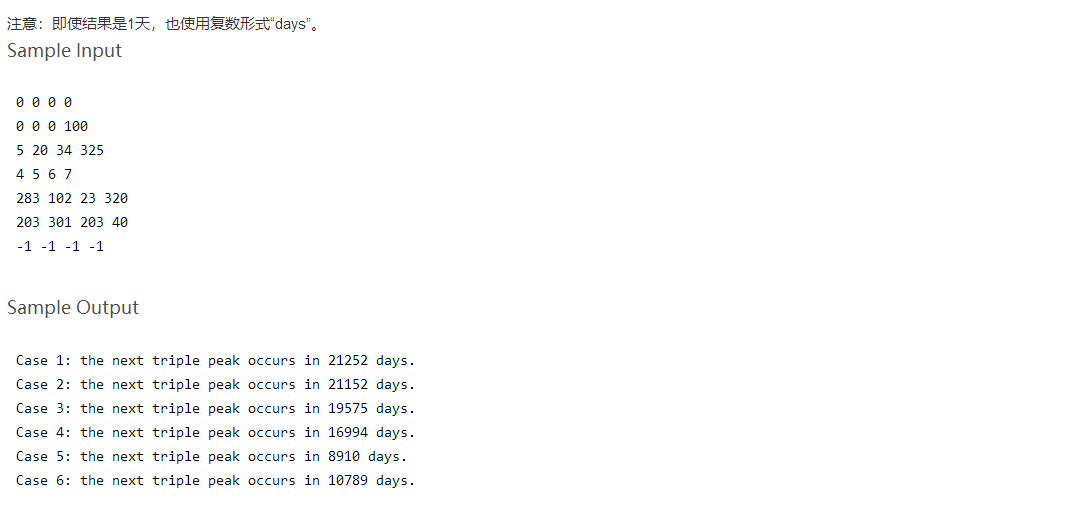
代码:
1 import java.util.ArrayList; 2 import java.util.List; 3 import java.util.Scanner; 4 5 public class POJ1006 { 6 7 public static void main(String[] args) throws Exception { 8 Scanner scanner = new Scanner(System.in); 9 int t = 1; 10 List<Long[]> aList = new ArrayList<Long[]>(); 11 List<Long> dList = new ArrayList<Long>(); 12 while(scanner.hasNext()){ 13 Long []a = {scanner.nextLong(),scanner.nextLong(),scanner.nextLong()}; 14 Long d = scanner.nextLong(); 15 if (a[0]==-1&&a[1]==-1&&a[2]==-1&&d==-1) { 16 break; 17 }else { 18 aList.add(a); 19 dList.add(d); 20 } 21 } 22 for (int i = 0; i < aList.size(); i++) { 23 Long[] a = aList.get(i); 24 long d = dList.get(i); 25 Long[] m = { (long) 23, (long) 28, (long) 33 }; 26 long res = MyGcd.linearEquationGroup(a, m); 27 while (res <= d) { 28 res += 21252; 29 } 30 System.out.println("Case " + (t++) + ": the next triple peak occurs in " + (res - d) + " days."); 31 } 32 } 33 34 private static class MyGcd { 35 static long x; 36 static long y; 37 38 /** 39 * 40 * @param a 余数组成的数组 41 * @param m 模组成的数组 42 * @return 43 * @throws Exception 44 */ 45 public static long linearEquationGroup(Long[] a, Long[] m) throws Exception { 46 int len = a.length; 47 if (len == 0 && a[0] == 0) 48 return m[0]; 49 50 for (int i = 1; i < len; i++) { 51 // 这里往前看是两个方程 52 long a2_a1 = a[i] - a[i - 1]; 53 long d = linearEquation(m[i - 1], -m[i], a2_a1); 54 // 现在的x是y1,用y1求得一个特解 55 long x0 = a[i - 1] + m[i - 1] * x; 56 long lcm = m[i - 1] * m[i] / d; 57 a[i] = (x0 % lcm + lcm) % lcm;// x0变成正数 58 m[i] = lcm; 59 } 60 // 合并完之后,只有一个方程 : x = a[len-1] (% m[len-1]) 61 //long d = linearEquation(1, m[len-1], a[len-1]); 62 return a[len - 1] % m[len - 1]; 63 } 64 65 public static long inverseElement(long a, long mo) throws Exception { 66 67 long d = linearEquation(a, mo, 1); 68 x = (x % mo + mo) % mo; 69 return d; 70 } 71 72 public static long linearEquation(long a, long b, long m) throws Exception { 73 long d = ext_gcd(a, b); 74 // m不是gcd(a,b)的倍数,这个方程无解 75 if (m % d != 0) 76 throw new Exception("无解"); 77 long n = m / d;// 约一下,考虑m是d的倍数 78 x *= n; 79 y *= n; 80 return d; 81 } 82 83 public static long ext_gcd(long a, long b) { 84 85 if (b == 0) { 86 x = 1; 87 y = 0; 88 return a; 89 } 90 long res = ext_gcd(b, a % b); 91 long x1 = x;// 备份x 92 x = y;// 更新x 93 y = x1 - a / b * y;// 更新y 94 return res; 95 } 96 97 } 98 99 }
结果:
