在前面的排序算法里面，我们发现每次找到一个最小的数都要进行很多次的比较，比如在n个数里面，我们如果想要找到最小的数，那么就需要比较 n-1次，那么我们想，能不能减少每次比较的次数呢。
其实发现是可以的，在前面的简单选择排序算法里面，我们每次找到最小的数后，剩余的一些数，其实有的是已经经过比较了的，所以在我们寻找第二小的数的时候，完全可以利用第一次的比较结果，但是由于我们没有把第一次比较的结果记录下来，所以我们在后面的比较过程中用不到，那么我们会想，能不能想办法把第一次比较的结果保存下来呢。办法肯定是有的，这就是今天我们要学习的堆排序。
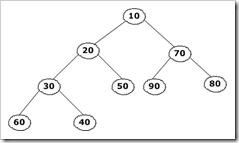
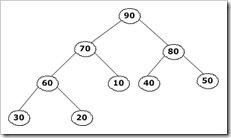
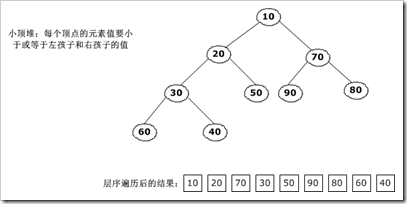
那么什么是堆排序呢，我们首先要弄清楚什么是堆。看下面的两个图，它们都是堆：
通过图我们可以看出，它们的根结点，要么比他们的左右孩子都大，要么比他们的左右孩子都小。这就是堆。具体的定义就是：
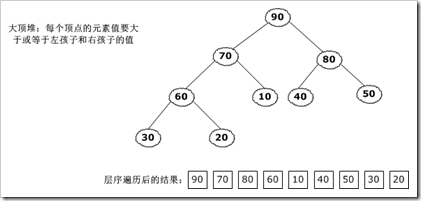
堆是具有以下性质的完全二叉树，每个结点的值都大于或者等于其左右孩子结点的值，叫做大顶堆，每个结点的值都小于或者等于其左右孩子结点的值，叫做小顶堆。由二叉树的一个性质，我们可以知道，一个完全二叉树，如果它的根结点位置是i，那么它左孩子位置就是2i,右孩子位置就是2i+1，所以大顶堆可以定义为ki>=k2i并且ki>=k2i+1,小顶堆的符号刚刚相反。
把堆进行层序遍历装入数据组，是如下结果：
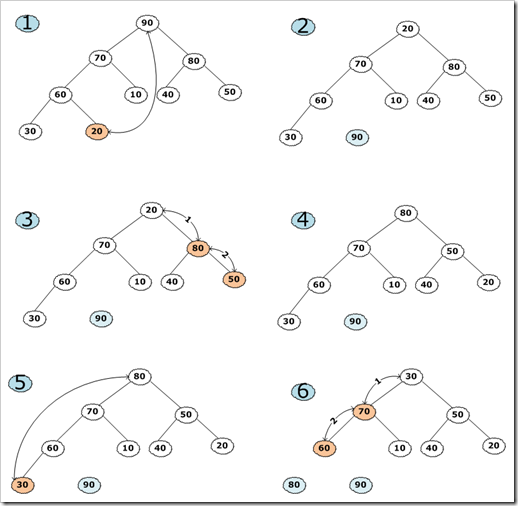
堆排序算法，就是把一个序列构造成一个大顶堆（此处以大顶堆为例），然后把堆顶的元素移走（其实就是跟最后的一个元素交换位置），然后把剩下的元素再重新构造成一个大顶堆，一直这样循环下去。最后整个序列就是有序的了。大家可以看下面的示意图：
1.把大顶堆最大的元素90移走（也就是把它与堆的最后一个数据进行交换）；
2.交换后，90成了最后的一个元素了，我们现在把它可以看做是进行排序了后的数，它现在与堆已经没有了关系，现在20成了堆顶的元素；
3.20成了堆顶元素之后，我们发现此时的堆不满足大顶堆的定义了，所以我们需要把剩下的元素进行调整，让它再次成为一个大顶堆。经过观察，我们发现，20需要与80进行互换，此时最顶上的一层满足大顶堆的定义，但是靠右边的子树不满足，所以我们要进行再次调整，也就是把20再与50交换，经过这样的调整后，整个树就又是一个大顶堆了。
4.按照第3步的分析，进行调整后，新堆又是一个大顶堆了。
5.重复步骤1，把新堆的第一个元素（也就是最大的那个元素80），和最后的一个元素（也就是30）进行交换。交换后，80相当于也是已经进行了排序的，它与原来的堆已经没有了关系。30现在成了堆顶的元素，然后重新步骤3，把剩下的数再次构造成一个顶堆，然后再重复5，一直这样下去，直到最后堆只剩下一个元素为止。这个时候，排序也已经排好了。
明白了堆排序的原理，要实现，我们必须要解决两个问题，一是如何把一个无序的列表构建成一个大顶堆；二是如何在输出一个元素后，再剩余的元素再构造成一个大顶堆。
对于第一个问题，如何把一个无序的列表构建成一个堆，我们看下面的示意图。
构造堆的过程其实是一个递归的过程，先把每一颗子树构造成堆，然后再来构造上一级的。
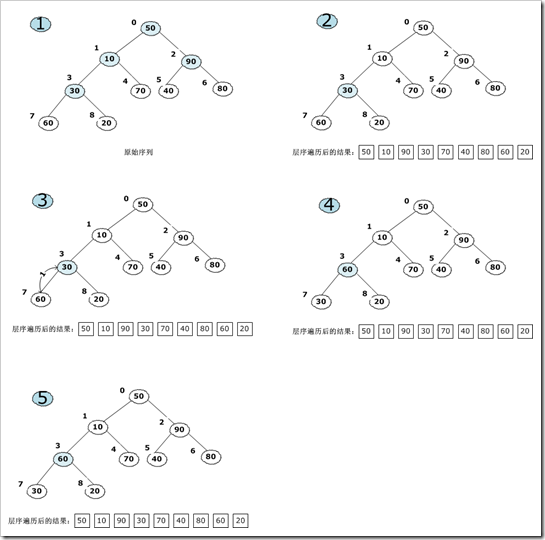
1.找出需要递归构造的子树，图1中标为浅蓝色的即为需要构造的子树的父结点，通过观察我们发现序号为0，1，2，3的结点需要进行构造，因为它们有子结点，其余的结点不需要构造，因为它们没有子孩子；
2.我们以序号为3的结点为例，把它构造成一个大顶堆，图2，3，4，5就是这样的一个构造过程，经过我们的观察发现，只需要把30与60交换位置即可，但是计算机没有这么聪明，你必须告诉它怎么算。计算机的实现过程，主要是，拿到一个结点，先比较它的左孩子和右孩子，找出最大的来，然后把这个最大的与父结点进行比较，如果比父结点大，那么不进行交换，否则进行交换，实现的过程看下面的代码：
public void HeapAdjust(List<int> list, int location, int arraryLength)
{
int temp, j;
temp = list[location];
//只有那些有孩子的结点才需要被构建，所以要循环遍历每一个有孩子的结点
//注意这里的序号要以经过层序遍历后它们在数组里面的位置为序号。
for (j = 2 * location+1; j < arraryLength; j = j*2+1)
{
//1.比较左孩子与右孩子的大小，找出它们中的最大者
if (j < arraryLength && list[j] < list[j + 1])
{
++j;//1.1如果左孩子比右孩子小，那么j++,j一直指向最大的那个孩子
}
//2.把最大的孩子与temp进行比较，temp此时装的是父结点的值
if (list[j] <= temp)
{
break;//2.1如果比父结点小，那么直接跳出循环
}
//3.否则把最大的数与父结点进行交换
list[location] = list[j];
location = j;
}
list[location] = temp;
}
有了这个方法之后，实现堆排序就比较简单，构建新堆的时候调用这个方法就可以了，我们下面再看堆排序的具体实现算法：
public List<int> HeapSort(List<int> sortList)
{
int i;
//1.先构建一个大顶堆
//把0，1，2，3这四个结点（有孩子的结点）分别构造成一个大顶堆
for (i = sortList.Count / 2-1; i >= 0; i--)
{
HeapAdjust(sortList,i,sortList.Count);
}
//2.把堆顶元素取出来，并且把剩下的元素再构造成一个大顶堆
for (i = sortList.Count-1; i >1; i--)
{
//2.1取堆顶元素的过程也就是与堆顶的元素与堆最后的一个元素进行交换
int temp = sortList[i];
sortList[i] = sortList[0];
sortList[0] = temp;
//2.2把剩下的元素再次构造成一个大顶堆
HeapAdjust(sortList,0,i-1);
}
return sortList;
}
整个堆排序的过程就是这样的，堆排序的时间复杂度为O(nLogn),具体的是怎么得来的，可以看《大话数据结构》书上面的分析，这里不多说了。