在接下来这篇博客中,我们将介绍如何获得从S到G的最短路径.
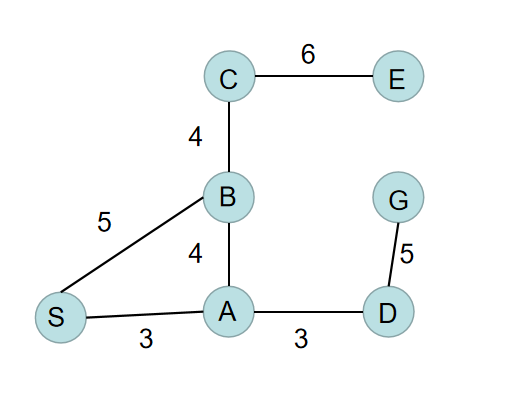
1.搜索树
我们可以以树的形式画出所有可能的路径:
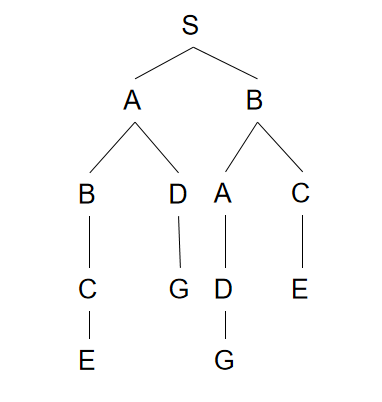
但是这种方法需要遍历所有的路径,效率非常低.
深度优先搜索
在S,面临的选择是A或B,按照惯例,我们总是往左走,也就是从S去A,然后到达,B,C,E,到达了死胡同之后,我们需要进行回溯,到A结点,选择另外一个分支D.依次这样循环下去,最终可以得到一个最短路径.
广度优先搜索
广度优先搜索是一层层地进行搜索,最后会发现自己得到了到达目标的路径.如上图所示,一层一层地计算,S可以到达A和B,从A可以到达B,D,这样一层一层的遍历,路径的数量会增长的非常快,但是最终我们也会得到一个最短路径.
爬山算法
对深度优先搜索和广度优先搜索的改进:如果一个结点扩展过了,我们就不需要再次对这个结点进行扩展.但是这样改进之后,算法依旧效率低下,那么我们是否可以找到一种更加知情的搜索算法呢?总体来说,我们希望离目标越来越近,所以如果我们面临选择,一边是一个离目标比较近的节点,另一边是离目标比较近的节点,我们总是希望选一个离目标较近的节点.把这加入到我们的搜索算法中后,我们就得到了另外一种算法:爬山算法.
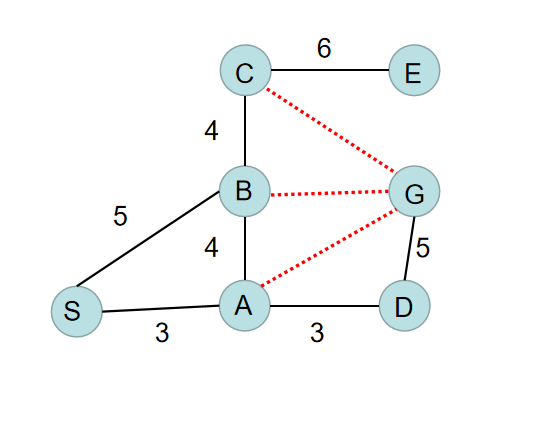
这个算法的搜索树如下:
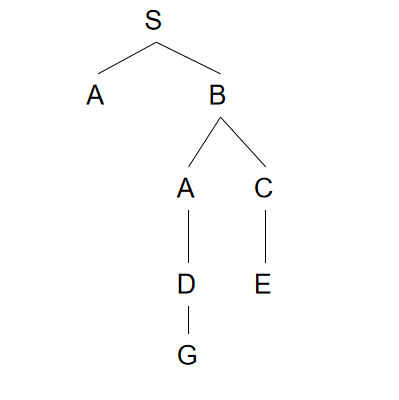
显然爬山法能大大提高搜索的速度,但不是最优的算法.
束搜索
束搜索是在爬山法的基础上将每一层中考虑的路径数限制在一个较小的固定数字上,例如这里我们可以设置束宽为2.
搜索树如下:
A*寻路算法
使用积累距离+直线距离来作为评判标准.
搜索树:

可容性的定义:H(X,G) <= D(X,G)(X同目标之间的估计距离 小于等于 X和目标之间的实际距离),
一致性的定义:|H(X,G) - H(Y,G)| <= D(X,Y)(X到目标的估计距离 - Y到目标的估计距离的绝对值 小于等于 X,Y之间的距离)
满足这两个条件,A*寻路算法才可以生效.