一、本文简介
本文的目的是简单明了的讲解KMP算法的思想及实现过程。
网上的文章的确有些杂乱,有的过浅,有的太深,希望本文对初学者是非常友好的。
其实KMP算法有一些改良版,这些是在理解KMP核心思想后的优化。
所以本文重点是讲解KMP算法的核心,文章最后会有涉及一些改良过程。
二、KMP算法简介
KMP算法是字符串匹配算法的一种。它以三个发明者命名,Knuth-Morris-Pratt,起头的那个K就是著名科学家Donald Knuth。
三、KMP算法行走过程
首先我们先定义两个字符串作为示例,被匹配串 S = "abcabdabcabeab",匹配串 T = "abcabeab"。
我们的目标就是确定S中是否包含T。
KMP算法的核心是分析匹配串 T 的特征,看看匹配串 T 能告诉我们什么信息。我把 T 着色,如下
T = "abcabeab"
现在看起来似乎比较明显了,三个着色点都是重复的 "ab",似乎这个 T 能告诉我们它有重复的子串"ab"可以利用。那么它们到底怎么用?先不讲具体怎么用,先走一遍KMP这个过程,但是大家需要留意这个"ab"。
1.

我们发现T在匹配成功 "abcab" 后到"e"时和S子串的"d"匹配不成功了。
这个时候我们可以得到的先验就是目前T匹配过的S子串,就是"abcab"。而T本身就是"ab"重复的。所以"abcab"可以直接跳到第二个重复"ab"的位置,因为"abcab"中其它字符串开头不可能产生和T对应的匹配,这是很直观的。
因此T应该直接后移三个位置,并且用第三位的"c"和S刚才不匹配的"d"进行比较。

可以发现,S匹配的过程是不会回退的。因此匹配过程是S从头到尾的一遍扫描(中间可能因为匹配成功退出),所以这个查找过程是O(N)的复杂度。
2.
此时的匹配串是 "ab", 它告诉我们目前匹配的是"ab"。这个不像"abcab"出现了重复"ab",所以我们知道包括S[5]的"d"之前的子串是垃圾串。因此跳过S[5]重新开始匹配T。
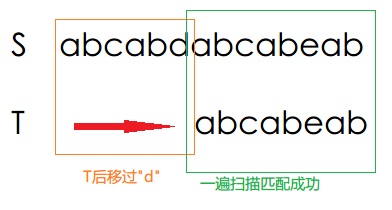
最后完成匹配,可见,这样一次对S的扫描完成了对T的查找。
那么对于机器如何实现?第四节会分析。
四、KMP算法核心解析
对于上面的过程,我们抽离出来的话,问题的根本就是对T串重复情况的一个判定。不管S是什么串,只要对T的构造模式分析清楚就可以完成上述跳转过程。
因此需要一个数组记录这个T的 模式函数。
这里先给出这个T的模式函数

1.每个字母对应模式函数的值就是匹配到当前位置 i 后,下一次T开始进行比较的下标。
2.而S的移动长度为 i - F(i-1)。
对应上面两个问题
1.比如上面的匹配到的 "abcab" ,是T匹配到 T[5] 即"e"的时候出错的。那么我们需要查看上一个字符的模式函数值,因为上一个函数值才代表了已经匹配的串。
发现F(4)=2,说明下次比较从T[2]即"c"开始。因为"abcab"有重复"ab",第一个"ab"不需要比较。
2.而S下标移动多少呢?S下标的移动即找到T的初试位置对应的S的下标。对应上面第二张图,S[3]和T的移动对应起来了。3的获得就是通过上面公式 5-F(4)得到的。其实这个结果和1得到匹配位置的思路是一样的,不过又向前移动对齐了开头。
为什么如此构造这个模式函数?
就是因为F值表示了对于位置 i, T[i]有无重复,并且重复下标的位置在哪(F[i])。既然我们获取了重复下标的位置,那么其它的相关值可以推出来了。
基于这个思路,再给出另外两个T串的模式函数值,帮助大家思考。
1.

2.

如何快速构造这个模式函数?
这个留给大家思考一下了,应该也比较直接了,注意是查找重复位置。如果不大明白,可以参考下面的代码。
五、KMP算法实现
再添加个例子帮助大家思考:
S1 = "aaaaaaaaaaaaaaaab" S2 = "aaaaafaaaaaaaaab" T = "aaaab"
对于S1和S2两种情况,应如何匹配。
代码如下:
1 /*
2 return val means the begin pos of haystack
3 -1 means no matching substring
4 */
5 int KMP(char *haystack, char *needle) {
6 // pre-process
7 if(haystack[0] == 0 && needle[0] == 0)
8 return 0;
9
10 int i, j, k, min, cur;
11
12 //construct F(t) in vector len
13 vector<int > len;
14 len.push_back(0);
15 for(i=1; needle[i] != 0; i++){
16 if(len[i-1] == 0){
17 if(needle[i] == needle[0])
18 len.push_back(1);
19 else
20 len.push_back(0);
21 }else{
22 if(needle[i] == needle[len[i-1]])
23 len.push_back(len[i-1]+1);
24 else
25 len.push_back(0);
26 }
27 }
28 // KMP finder
29 j = 0;
30 for(i=0; haystack[i] != 0; ) {
31 // matching
32 for(; needle[j] != 0; j++) {
33 if(haystack[i+j] != needle[j])
34 break;
35 }
36 //finded
37 if(needle[j] == 0)
38 return i;
39 else{ // jump
40 if(j){
41 cur = j - len[j-1];
42 i += cur;
43 j = len[j-1];
44 }else{
45 j = 0;
46 i++;
47 }
48 }
49 }
50 //match failed
51 return -1;
52 }
六、KMP算法改进
KMP算法有一些改进版本加速查找,一般可以通过S串中的一些信息加速匹配过程。
比如若 S = "aaaaaaaafaaaaaaaaaaaab", T = "aaaaaaab"。
在查找过程中,S中间的 "f" 起到了阻挡作用。但是由于我们只是考虑T的先验信息,遇到"f" 不匹配会导致T每次后移一步进行新的匹配,直到T的开头碰到了"f"。
但是如果我们加入"f"这个原串S的信息,由于"f" != "b" && "f" != "a" && i-1 = F(i-1) ,所以直接跳到"f"后进行新的匹配会更快速的查找。
但是这些改进都是基于KMP基础算法之上的,因此把握核心要点不仅省时省力,更能有效扩展。
七、参考
[1] 《字符串匹配的KMP算法》 http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html
[2] 算法导论
转载请注明出处~ http://www.cnblogs.com/xiaoboCSer/p/4237941.html