问题、问题实例、算法:
在考虑问题时,需要清晰的区分问题、问题实例和算法三个概念,并理解它们之间的关系。
问题:一个问题W是需要解决(需要用计算求解)的一个具体需求。例如判断任一个正整数N是否为素数,虽然可以严格定义“问题”的概念,但在这里还是想依靠读者的直观认识。总而言之,现实世界中存在许多需要用计算解决的问题,它们是研究和实现算法的出发点。
问题实例:问题W的一个实例w是该问题的一个具体例子,通常可以通过一组具体的参数设定。
算法:解决问题W的一个算法A,是对一种计算过程的严格描述。对W的任何一个实例w,实施算法A描述的计算过程,就能得到w的解。
算法的实质:
一个算法是对一种计算过程的一个严格描述,人们通常认为算法具有如下性质:
有穷性:一个算法的描述应该由有限多条指令或语句构成。也就是说,算法必须能用有限长的描述说清楚。
能行性:算法中指令(语句)的含义严格而且简单明确,所描述的操作(计算)过程可以完全机械地进行。
确定性:作用于所求解问题的给定输入(以某种描述形式给出的要处理问题的具体实例),根据算法的描述将产生出唯一的确定的一个动作序列。使用算法就是把问题实例送给它,通过确定性的操作序列,最终得到相应的解。
终止性(行为的有穷性):对问题的任何实例,算法产生的动作序列都是有穷的,它或者终止并给出该问题实例的解,或者终止并指定给定的输入无解。
输入/输出:有明确定义的输入和输出。
算法的描述:
常见的描述形式:
采用自然语言描述;
采用自然语言描述中结合一些数学记法或公式的描述形式;
采用严格定义的形式记法形式描述;
用类似某种编程语言的形式描述算法过程;
采用某种伪代码形式。
程序可以看作严格计算装置能够处理的语言描述的算法,由于它是算法的实际体现,又能在实际计算机上执行,因此被称为算法的实现。
算法设计与分析:
算法设计:就是从问题出发,通过分析和思考最终得到一个能解决问题的过程描述的工作工程。算法设计显然是一种创造性工作,需要靠人的智慧和经验,不可能自动化。实际问题千变万化,解决它们的算法的表现形式也多种多样。但是许多算法的设计思想有相似之处,相关工作也有规律可循。人们深入研究了前人在算法领域的工作经验和成果,总结出了一批算法设计的重要思路和模式。对算法设计方法做分类研究,可以给后人的学习提供一些指导。已有的设计经验和模式可能提供一些有用的线索和启发,供人们在设计解决新问题的新算法时参考。
常见的算法设计模式:
枚举法:根据具体问题枚举出各种可能,从中选出有用信息或者问题的解。这种方法利用计算机的速度优势,在解决简单问题时十分有效。
贪心法:如前所述,根据问题的信息尽可能做出部分的解,并基于部分解逐步扩充得到完整的解。在解决复杂问题时,这种做法未必能得到最好的解。
分治法:把复杂问题分解为相对简单的子问题,分别求解,最后通过组合子问题的解的方式得到原问题的解。
回溯法(搜索法):专指通过探索的方式求解。如果问题很复杂,没有清晰的求解路径,可能就需要分步骤进行,而每一步骤又可能有多种选择。在这种情况下,只能采用试探的方式,根据实际情况选择一个可能方向。当后面的求解步骤无法继续时,就需要退回到前面的步骤,另行选择求解路径,这种动作称为回溯。
动态规划法:在一些复杂情况下,问题求解很难直截了当进行,因此需要在前面的步骤中积累信息,在后续步骤中根据已知信息,动态选择已知的最好求解路径(同时可能进一步积累信息)。这种算法模式被称为动态规划。
分支限界法:可以看作搜索方法的一种改良形式。如果在搜索过程中可以得到一些信息,确定某些可能的选择实际上并不真正有用,就可以及早将其删除,以缩小可能的求解空间,加速问题求解过程。
算法分析:只要任务就是弄清算法的资源消耗。
数据结构:
研究数据之间的关联和组合的形式,总结其中的规律性,发掘特别值得注意的有用结构,研究这些结构的性质,进而研究如何在计算机里实现这些有用的数据结构,以支持相应组合数据的高效使用,支持处理它们的高效算法。
抽象定义与重要类别:
首先抽象地考虑数据结构的概念。从逻辑上看,一个数据结构包含一集数据元素,是一个有穷集,在这些元素之间有着某些特定的逻辑关系。按照这种观点抽象地看,一个具体的数据结构就是一个二元组:
D = (E, R)
其中的 E 是数据结构 D 的元素集合,是某个数据集合 ε 的一个有穷子集,而 R ∈ E * E 是 D 的元素之间的某种关系,对于不同种类的数据结构,其元素之间的关系具有不同性质。
一些典型的数据结构:
集合结构:其数据元素之间没有需要关注的明确关系,也就是说关系 R 是空集。这样的数据结构也就是其元素的集合,只是把一组数据元素包装为一个整体。这就是最简单的一类数据结构。
序列结构:其数据元素之间有一种明确的先后关系(顺序关系)。存在一个排位在最前面的元素,除了最后的元素外,每个元素都有一个唯一的后继元素,所有元素排列成一个线性序列。关系 R 就是这里的线性顺序关系,这种结构也被称为线性结构,一个这样的复杂数据对象就是一个序列对象。序列结构还有一些变形,如环形结构和 ρ 形结构。其特点是每个元素只有(最多)一个后继。
层次结构:其数据元素分属于一些不同的层次,一个上层元素可以关联着一个或者多个下层元素,关系 R 形成一种明确的层次性,只从上层到下层(通常也允许跨层次)。层次关系又可以分为许多简单或复杂的子类别。
树形结构:层次结构中最简单的一种关系是树形结构,其特点是在一个树形结构中只有一个最上层数据元素,称为根,其余元素都是根的直接或间接关联的下层元素。进一步说,除根元素之外的每个元素,都有且仅有一个上层元素与之关联。树形数据结构简称为叔,相应的复杂数据对象称为树形对象。
图结构:数据元素之间可以有任意复杂的相互联系。数学领域中的图概念是这类复杂结构的抽象,因此人们把这样的结构称为图结构,把这样的复杂对象称为图对象。
内存单元和地址
计算中直接使用的数据保存在计算机的内存储器(简称内存)。内存是CPU可以直接访问的数据存储设备。与之相对应的是外存储器,简称外存,如磁盘、光盘、磁带等。保存在外存里的数据必须先装入内存,而后CPU才能使用他们。
Python对象和数据结构
python变量和对象:高级语言里的变量是内存及其地址的抽象。变量本身也需要在内存中安排位置,每个变量占用若干个存储单元。语言系统需要有一套系统化的安排方式处理这个问题。
在python程序里,可以通过初始化(或提供实参)给变量(或函数参数)约束一个值,还可以通过赋值修改变量的值。这里的值就是对象,给变量约束一个对象,就是把该对象的标识(内存位置)存入该变量。
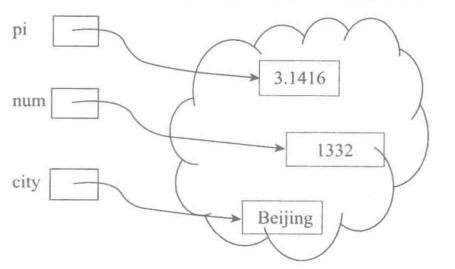
python变量的值都是对象,也可以是基本整数、浮点数等类型的对象,也可以是组合类型的对象,如list等。程序中建立和使用的各种复杂对象,包括python函数等,都基于独立的存储块实现,通过连接相互关联。程序里的名字(变量、参数、函数名等)关联着作为其值得对象,这种关联可以用赋值操作改变。
python语言中变量的这种实现方式成为变量的引用语义,在变量里保存值(对象)的引用。采用这种方式,变量所需的存储空间大小一致,因为其中只需要保存一个引用。
python对象的表示
python语言的实现基于一套精心设计的链接结构。变量与其值对象的关联通过链接的方式实现,对象之间的联系同样也通过链接。一个复杂对象内部也可能包含几个字部分,相互之间通过链接建立联系。例如,一个list里包含了10个字符串,那么在实例中,在这个list对象里就会记录这10个字符串的链接关系。
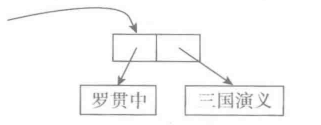
实际上,各种数据对象的具体表示方式,将对相关对象的各种操作的效率产生直接影响,间接影响着用python开发的程序的效率。
python的几个标准数据类型
list(表),list对象可以包含任意多个任意类型的元素,元素访问和修改都是常量时间操作。list对象可变,可以任意增删元素。
tuple(元祖),在保存元素和元素访问方面的性质与表类似,但其对象是不可变对象,只能在创建时构造出来,不能逐步构造。
dict(字典),支持基于关键码的数据存储和检索,这里的关键码只能是不变对象。如果关键码是组合对象,其元素仍然必须是不可变对象。在一个字典里可以容纳任意多的关键码/值关联,支持高效检索。