今天是赵和旭老师的讲授~
状态压缩 dp
状态压缩是设计 dp 状态的一种方式。
当普通的 dp 状态维数很多(或者说维数与输入数据有关),但每一维总量很少时,可以将多维状态压缩为一维来记录。
这种题目最明显的特征就是:都存在某一给定信息的范围非常小(在 20 以内),而我们在 dp 中所谓压缩的就是这一信息。
(或者是在做题过程中分析出了某一信息种类数很少)

我们发现这个 m 是非常小的,这样就可以启发我们对每一行 2m 状态压缩。
设 dp [ i ][ S ] 表示到了第 i 行,第 i 行的状态是 S 的方案数是多少。
其中 S 的第 j 位为 1,表示 i 这行第 j 位放了一个棋子。
状态转移:dp [ i ][ S ] = ∑ { dp [ i-1 ][ S' ] | S & S' == 0 }。
你会发现这样记录很暴力,状态数是与 m 相关的指数级的,但同时也就是因为 m 小我们就确实可以这么做。
这也正好映照了之前的:
最明显的特征就是:都存在某一给定信息的范围非常小!
其实本质就是很暴力的记录状态,只不过利用了题目本身的特殊条件 (这一维很小),使得我们并不会因此复杂度过高。
同时也就是说,如果题目本身没有这样一个较小的信息,就不能应用状态压缩。
所以在接下来的题目中大家可以更注意一下题目所给的条件。
状态压缩 dp 肯定是有一维是指数级的,这正是状态压缩的特点。

多一个条件,加一个维度。
f [ i ][ k ][ S ] 表示 k 个放完前 i 行,第 i 行的放置状态为 S 的方案数。
S 为一个 n 位二进制数,表示第 i 行的每一位上是否有棋子。
由于棋子不能相邻,也就是这个二进制不能有相邻的 1,所以可以先对求
出对一行来说合法的状态(合法的二进制数有哪些)。
转移:
判断上下相邻是否有 1:s' & s == 0;
判断往左攻击的范围内是否有 1:(s' << 1)& s == 0;
判断往右攻击的范围内是否有 1:(s' >> 1)& s == 0;
更简单的写法:
f [ i ][ k+cnt ( S ) ][ S ] += f [ i-1 ][ k ][ T ],( ( T | (T<<1 ) | ( T>>1 ) ) & S ) ==0
(巧用位运算!)
时间复杂度O ( n3 * 状态数2 ) < O ( n3 * 22n ) );
(实际上状态数是 Fibonacci)
位运算在这里发挥了大的用途
状态压缩有 k 进制的,论题目出现频率的话二进制的题目居多,同时因为计算机本身存储数就是以二进制方式,所以二的幂次的进制处理很方便, 状态压缩 dp 中有时巧用位运算可以产生很好的效果,比如本题,我们就 不需要 O ( n ) 枚举每一位判断是否冲突了。
位运算
1:( s & (1 << i ) ):判断第 i 位是否是 1;
2:s = s | ( 1 << i ):把第 i 位设置成 1;
3:s = s & ( ~ ( 1 << i ) ):把第 i 位设置成 0;
( ~:是按位取反,包括符号位 )
4:s = s ^ ( 1 << i ) :把第 i 位的值取反;
5:s =s & ( s – 1 ):把一个数字 s 二进制下最靠右的第一个 1 去掉;
6:for (s0 = s; s0; s0 = (s0 - 1) & s): 依次枚举 s 的子集;

7:x&-x 取出x最低位的1。

在输入的时候将每个点的入度处理出来,状压一下。
dp [ s ] 表示当前 s 集合中的点都已经在拓扑序中的方案数,转移考虑枚举下一个点选什么,下一个选的点要满足它在 s 中的点选完后的入度为 0,也就是指向它的点都已经加进拓扑序里了,转移到 dp [ s | ( 1 << i-1 ) ] 。
选的条件就是:S & in [ i ] = in [ i ];
这个有没有位运算的优化呢?
复杂度 O ( 2n * n ) 。

记 g [ x ] 表示将 x 中的 2 , 3 因子去除后得到的值,若 g [ x ] != g [ y ],那么 x 与 y 互不影响。对于互相有影响的一组数,一定能表示成 q * 2a * 3b ( q 为常数 ) 。对每种 q 分别求解,再相乘即可。
以 q=1 为例,可把所有 2a * 3b 以 a , b 为行列画成一个三角形棋盘,求棋盘上放不能相邻的棋子的方案数。我们会发现这个三角形最宽的层最多只有 11 个,所以可以状态压缩。
31 32 33 34 ……
21*31 21*32 21*33 21*34 ……
22*31 22*32 22*33 22*34 ……
23*31 23*32 23*33 23*34 ……
…… …… …… …… ……
这也就对应了:做题过程中分析出了某一信息的种类数很少。
当 q>1,等价于 q' = 1 && n' = n/q。
剪枝:对于 n/q 相同的 q,可以避免重复计算来加速。

两头猪加上原点即可确定抛物线,于是不同的抛物线只有 O ( n2 ) 种。
设 f [ S ] 为已经消灭的猪的集合为 S 时的最少次数,t [ i ] 表示每条抛物线能打的猪,暴力的转移方法为依次枚举抛物线去更新所有 f,这样做时间复杂度为 O ( n2 * 22 ) 。
更快的转移方法为从小到大枚举 S,每次打掉编号最小的还没消灭的猪, 由于包含该猪的抛物线只有 O ( n ) 种,所以时间复杂度为 O ( n * 2n )。
选择抛物线的限制:dp [ s ^ s' ]
其实就避免一些重复的计算。

设 f [ s ] 表示 s 这个集合能否被第一辆车一次运走,g [ s ] 表示 s 这个集合能否被第二辆车一次运走,t [ s ] 表示 s 这个集合能否被两辆车一次运走;
找出所有状态 (1..... ( 1<<n ) -1)中选出可以用两辆车一次运完的状态(枚举全部);
把每个状态都看作一个物品,重量为该状态的总重量,价值为 1,其实我们就是求最少选几个不相交的集合能够覆盖全集。
求解 01 背包,dp [ ( 1<<n ) - 1 ]为最优解。
转移方程: dp [ s ] = min ( dp [ s ] ,dp [ s^t ] + 1 ) 其中 t 集合内的元素可以被一次运完。
这个复杂度是 O ( 3n )。
实际上如果我们固定 t 集合包含 s 最低位的 1,这样能避免重复运算,复杂度降约为 O ( 3 n-1 ) 枚举子集 3n也是很常见的状压dp!!

首先其实最终肯定是把这些鹿分成一些组,每一组内通过组的大小减一次操作来满足题目要求的条件。注意对于一个组,我们将所有的角排序, 第 2 * i - 1 和 2 * i 个要保证之差小于等于 C,才是合法的一组。
考虑到一个集合内最多的交换次数为:元素个数 - 1;
其实就是选尽量多合法的组并起来等于全集,枚举子集的状态压缩 dp 即可。
dp [ i ] = max { dp [ j ] + dp [ i ^ j ] | j 是 i 的一个子集 } 。
一点总结
像这种某些集合是可行的,且每个集合有一个价值,然后我们要选择一 些不相交的集合并起来等于全集,每个选择的集合都要求可行,且希望总权值尽量大。
这一类 dp 往往是要用到状态压缩 dp 同时利用枚举子集来进行转移,转移的过程中常常可以控制最低位的 1 必选来减少 dp 重复的计算。像这前两道题,以及之前的愤怒的小鸟也一样,只不过小鸟那题通过分析题目的特 点使得我们在转移的过程中不需要枚举全部的子集,只需要枚举 n 个抛物线即可。

三进制状态压缩
设 dp [ S ][ i ] 表示到过点的情况集合为 S,S 是个三进制数,第 i 为 0/1/2 分别表示到过次数。i 为当前所在的点。转移的话就考虑下一步走到那条边就好。
答案就是 dp [ 3n -1 ][ i ] 的最小值。
会二进制的表示,三进制想起来应该很自然吧。
其实是 TSP 旅行商问题的一种较为麻烦的形式。
关于时间复杂度
N=20 一般是 2n 或者 n * 2n 。
N<=16 大概率是 3n,约是 4 * 107,那很可能做法就和之前讲枚举子集有关了。
N<=15 大概率是 3n 或者 n * 3n 。
随堂练习

贪心来看显然要用尽量用最大的那几个,所以先把包从大到小排序。
设 f [ S ] 为把集合 S 放入包后至少要用到第几个包,g [ S ] 记录此时用到的最后 一个包能剩余的最大体积。
转移时枚举接下来放哪个物品即可。
时间复杂度 O ( n * 2n );
总结
基本的状态压缩 dp。
位运算在状压 dp 中,经常能发挥大的作用,灵活的使用位运算可以降低算法的时间复杂度。
选择一些不相交的可行集合并起来等于全集,且希望选出集合总权值尽量大,通常要 O ( 3n ) 枚举子集的技巧。而通过强制枚举的子集包含最低位的 1,可以避免重复的计算。
通过一个类 TSP 问题,对三进制状态压缩的初探。
dp 常见优化方式
noip 范围内的 dp 优化方法
加速状态转移:
1:前缀和优化;
2:单调队列优化;
3:树状数组或线段树优化;
精简状态:
3:精简状态往往是通过对题目本身性质的分析,去省掉一些冗余的状态。 相对以上三条套路性更少,对分析能力的要求更高 。
前缀和优化

排列题的一个套路,我们从小到大依次把数字插入到排列中,以这 个思路进行 dp。
这个问题设计动态规划的方法就是最基本,最自然的。
我们设 dp [ i ][ j ] 表示插入了前 i 个数,产生的逆序对为 j 的排列的方案数, 转移时就考虑 i+1 的那个数插在哪一个位置就好,因为它比之前的都要大,插在最后面就 dp [ i+1 ][ j+0 ] += dp [ i ][ j ],如果时最后一个数前面就是 dp [ i+1 ][ j+1 ] += dp [ i ][ j ],倒数第 2 个数前面就是 dp [ i+1 ][ j+2 ] += dp [ i ][ j ],依次类推。这个是从前向后更新。
dp [ i ][ j ] = Σ(0 <= k <= i-1) dp [ i-1 ][ j-k ];
我们如果考虑 dp [ i ][ j ] 能从哪些状态转移过来,就可以前缀和优化。
方程:
![]()
我们设:
![]()
则 dp [ i ][ j ] = f [ i-1 ][ j ] - f [ i-1 ][ j-i ]
这样我们通过记录前缀和,将转移优化成 O (1)
其实这题复杂度还可做到 n 和 k 均是 100000:loj6077(2017年山东省队集 训题)
在这个 dp 基础上,做容斥原理,通过之前讲的整数划分的模型 dp 求出容斥系数即可。
单调队列优化
基本形式,适用范围
单调队列维护 dp,一般就是把一个 O ( N ) 转移的 dp 通过单调队列优化成一 个均摊 O ( 1 ) 转移的式子。
式子形如:dp [ i ] = max { f ( j ) } + g [ i ](这里的 g [ i ] 是与 j 无关的量),且 j 的取值是一段连续区间,区间端点的两端随着 i 增大而增大的区间。
(同时如果这个可行的区间左端点固定,我们就可以通过之前讲的记录前缀最小值来处理)
这里的 f ( j ) 是仅和 j 有关的项。以下是常见的一维和二维的情况。
dp [ i ] = max { dp [ j ] + f ( j ) } + g [ i ] 或者 dp [ level ][ i ] = max { dp [ level-1 ][ j ] + f ( j ) } + g ( i )
这样的题我们就可以做单调队列优化 。

设 f [ i ][ j ] 表示到第 i 天手里持有 j 的股票的最大收益,那么第 i 天有三种操作:
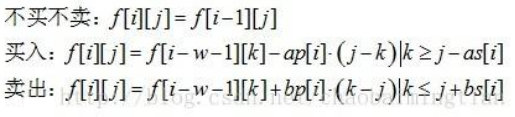
对于买入,我们对其变形:

那么可以用单调队列维护 f [ i-w-1 ][ k ] + ap [ i ] * k(因为对于固定的 i,ap [ i ] 是固定的),这样 f [ i ][ j ] 就能做到 O ( 1 ) 求得,而不必枚举 k。卖出也一样。
买入部分的代码实现:
id 和 q 数组构成单调队列。 id 存的是队首的下标。 q 存的是买队首的收益。 记下标是为了窗口移动的时候判断队首是否还合法,而求最大收益也肯定是要记个最大值。

之前讲的过一些问题
1:O( N * M ) 的多重背包。
2:基环树求直径。
单调队列优化和前缀和优化的对比
单调队列优化 dp 跟前缀和优化 dp 差不多一个思路,转移的合法点集都是 一个区间。
只不过,单调队列优化 dp 是当你在最优化 dp 值时候和一段区间有关。
而,前缀和优化 dp 是在计数的时候和一段区间有关。

根据题意,我们很容易得出下面的转移方程
1. f [ i ] = min ( f [ j ] + 1) ( i-k ≤ j < i )
2. f [ i ] = min ( f [ j ] ) ( i-k ≤ j < i && h [ j ] > h [ i ] )
发现上面那个东西用单调队列直接搞定,但下面那个不太好搞。不过发现由于 h [ j ] > h [ i ] 对答案的贡献至多为1,所以原来如果 f [ j ] < f [ j‘ ],那么算上 h [ j ]和 h [ j’ ] 的影响后 j 仍然不会比 j‘ 更差,于是直接维护一个 f 递增的单调队列,其中当 f 相同的时候使 h 递减就行了。
这么做,主要利用了题目中高和矮转移的费用只差1,这样如果矮的 f [ i ] 小的话,就算加上 1 也只是和高的 f 值相同不会更差。如果费用更高就不能用这个方法了。
树状数组或线段树优化

先按照每个区间的左端点排序;
dp [ i ][ j ] 考虑前 i 个区间覆盖到 j 的方案数;

区间求和,区间乘 2,单点赋值,考虑线段树优化。
这三个技巧往往就是 dp 列出式子来之后,观察一下式子,你发现它满足 对应优化的模型,所以我们就单调队列或者前缀和或者线段树优化了。
对思维的要求并不高。
分析题目性质精简状态
精简状态
这个对题目性质的分析能力要求还是比较高的。
需要挖掘题目的性质,特点等等。
不能算很套路的内容,需要多做题感受。

其实可以理解为从小渊到小轩传两次。
最暴力的做法:设 dp [ i ][ j ][ k ][ l ] 是第一张纸条到达 ( i , j ),第二张到达 ( k , l ) 时最大权值。那么方程就是:
dp [ i ][ j ][ k ][ l ] = map [ i ][ j ] + map [ k ][ l ] + max ( dp [ i - 1 ][ j ][ k - 1 ][ l ] , dp [ i -1 ][ j ][ k ][ l - 1] , dp [ i ][ j - 1 ][ k -1 ][ l ] , dp [ i ][ j -1 ][ k ][ l -1] );
还有一点注意的是,如果 i == k && j == l,也就是第二张走了第一张的路径, 那么就要减去,dp [ i ][ j ][ k ][ l ] -= map [ i ][ j ];
接下来枚举每个 i , j ,k , l ,最后输出 dp [ m ][ n ][ m ][ n ] 就行了,但这样做时间复杂度是 O ( n4 ),其实我们可以让两个路线并行走,同时走。
而既然第一张与第二张是同时走,那么我们知道他们的步数是一样的, 步数 = 横坐标+纵坐标,所以只需枚举 i , j , k,就能计算出 l,只需三重循环, 时间就变成了 O ( n3 );
dp [ i ][ j ][ k ] = map [ i ][ j ] + map [ k ][ i+j-k ] + max ( dp [ i - 1 ][ j ][ k - 1 ] , dp [ i -1 ][ j ][ k ] , dp [ i ][ j - 1 ][ k -1 ] , dp [ i ][ j -1 ][ k ] );
T1(最难最毒瘤的题目,建议最后食用)


这道题的实质其实是在一棵树上,每个根到叶子的路径所经过的字符其实就是某个汉字所对应的字符串;
为了方便起见,我们设 ha 的长度为 2,a 的长度为 1,这样的话每个叶子的深度就是所对应的汉字的长度;
贪心一下我们就是把层数最少的给出现最多的,层数最多的给出现最少的汉字;
那么我们的任务就是找一棵叶子个数至少为 n 的树,使得它所贡献的答案最小。
我们从根开始找:
设 dp [ i ][ x ][ y ][ k ] 表示我们目前已经到了第 i 层,第 i 层有 x 个结点(是叶子还是芽我们也不知道),第 i+1 层有 y 个结点,我们已经确定了 k 个叶子了(不包括第 i 层);
枚举 p,在 x 层里有 p 个变成了叶子,那么会收获 i * (sum [ k+p ] - sum [ k ]);
转移到 :dp [ i+1 ][ x+y-p ][ x-p ][ k+p ] + i * (sum [ k+p ] - sum [ k ]);(我们光让 x 长叶子)
dp [ x ][ y ][ k ] :x 是当层的芽,y 是上一层的芽,k 是叶子;
dp [ y+x-p ][ x-p ][ k+p ];
dp [ x ][ y ][ k ] :
1. dp [ x-1 ][ y ][ k+1 ];没有任何贡献
2. dp [ y+x ][ x ][ k ] + (sum [ n ] - sum [ k ]);
T2(无毒无害最简单的题目)

数位 dp 的题都炒鸡简单?
这个题如果还是按照我们之前做数位 dp 的套路:按照每一位填什么,过程中维护各位数字和以及最后数字的大小的话,发现是无法边求边取模的;
那么我们就枚举最后的各位数字和是多少!
这样的好处就是我们能够确定过程中的模数了,最后只需要保证各位数字之和等于我们事先设定的那个数。
我们设 dp [ i ][ sum ][ mod ] :我们正在填第 i 位,还没填的数位(包括第 i 位)之和是 sum,前面已经填的数模数位之和的余数是 mod;
考虑怎么转移:
我们先枚举 S(各位数字之和),那么一位都没有填的时候:dp [ len ][ S ][ 0 ];
假设我们第 i 位填了 x,则 dp [ i ][ sum ][ mod ] -> dp [ i-1 ][ sum-x ][ ( mod + x * C [ i-1 ] ) % S ];
C [ i-1 ] 表示的是 ci-1 ,c 是题目中给出的 c 进制;
这个过程可以利用记忆化搜索来实现;
T3



不可能存在两个集合交集都为空;
如果存在一个交集为空,那么我们取前 k-1 长的线段单独放到一个集合里就好了;
我们把不包含其他线段的所有线段拿出来,如果我们将它们的左端点递增排序,那么它们的右端点也是递增的!
设 dp [ i ][ j ] 前 i 条线段分成 j 组的最大值;
dp [ i ][ j ] = max ( dp [ x ][ j-1 ] + R [ x+1 ] - L [ i ] ) | R [ x+1 ] > L [ i ] ;
时间复杂度 O(n3),我们可以单调队列优化。
剩下的包含其他线段的线段,我们取出长度前 k-q 个(q 是不包含其他线段的线段数)