ACM-ICPC 2018 沈阳赛区(网络赛)

D.Made In Heaven

One day in the jail, F·F invites Jolyne Kujo (JOJO in brief) to play tennis with her. However, Pucci the father somehow knows it and wants to stop her. There are

JOJO starts from spot

Input

There are at most

The first line contains two integers

The second line contains four numbers

Then

It is guaranteed that for any two spots there will be only one directed road from spot

All the test cases are generated randomly.

Output

One line containing a sentence. If it is possible for JOJO to arrive at the destination in time, output "yareyaredawa" (without quote), else output "Whitesnake!" (without quote).

样例输入

样例输出

yareyaredawa

题目来源

ACM-ICPC 2018 沈阳赛区网络预赛

题目思路：求个第k短路就好了

#include <bits/stdc++.h>

using namespace std;
const int INF = 0x7FFFFFFF;
const int MAXN = 1010;
const int MAXM = 105000;

int S, E, K, T;

struct Edge {
    int u, v, c, next, next1;
    Edge() {}
    Edge(int u, int v,int c):u(u), v(v), c(c) {}
} edge[MAXM * 4];

int first[MAXN], first1[MAXN], sign;
int n, m;
int dis[MAXN];
bool vis[MAXN];

struct Node {
    int v, c;
    Node() {}
    Node(int v, int c):v(v), c(c) {}
    bool operator < (const Node& a) const {
        return c + dis[v] > a.c + dis[a.v];
    }
};

void init() {
    memset(first, -1, sizeof(first));
    memset(first1, -1, sizeof(first1));
    sign = 0;
}
void addEdge(int u, int v, int c) {
    edge[sign] = Edge(u, v, c);
    edge[sign].next1 = first1[v];
    first1[v] = sign;
    edge[sign].next = first[u];
    first[u] = sign++;
}

priority_queue<Node>que;

void dijkstra(int s) {
    memset(vis, 0, sizeof(vis));
    for(int i = 1; i <= n; i++) {
        dis[i] = INF;
    }
    while(!que.empty()) { que.pop(); }
    dis[s] = 0;
    que.push(Node(s, 0));
    while(!que.empty()) {
        Node cur = que.top();
        que.pop();
        if(!vis[cur.v]) {
            vis[cur.v] = 1;
            dis[cur.v] = cur.c;
            for(int i = first1[cur.v]; ~i; i = edge[i].next1) {
                if(dis[edge[i].u] > dis[cur.v] + edge[i].c) {
                    que.push(Node(edge[i].u, edge[i].c + cur.c));
                }
            }
        }
    }
}

int a_star(int src) {
//    priority_queue<Node>que;
    while(!que.empty()) { que.pop(); }
    que.push(Node(src, 0));
    while(!que.empty()) {
        Node cur = que.top();
        que.pop();
        if(cur.v == E) {
            if(K > 1) {
                K--;
            }
            else {
                return cur.c;
            }
        }
        for(int i = first[cur.v]; ~i; i = edge[i].next) {
            que.push(Node(edge[i].v, cur.c + edge[i].c));
        }
    }
    return -1;
}

int main() {
    int u, v, c;
    while(~scanf("%d%d",&n, &m)) {
        init();
        scanf("%d %d %d %d", &S, &E, &K, &T);
        while(m--) {
            scanf("%d %d %d",&u, &v, &c);
            addEdge(u, v, c);
        }
        dijkstra(E);
        if(dis[S] == INF) {
            puts("Whitesnake!");
            continue;
        }
        if(S == E) {
            K++;
        }
        int res = a_star(S);
        if(res == -1) {
            puts("Whitesnake!");
            continue;
        }
        if(res <= T) {
            puts("yareyaredawa");
        } else {
            puts("Whitesnake!");
        }
    }
    return 0;
}

View Code

"Oh, There is a bipartite graph.""Make it Fantastic."

X wants to check whether a bipartite graph is a fantastic graph. He has two fantastic numbers, and he wants to let all the degrees to between the two boundaries. You can pick up several edges from the current graph and try to make the degrees of every point to between the two boundaries. If you pick one edge, the degrees of two end points will both increase by one. Can you help X to check whether it is possible to fix the graph?

Input

There are at most

For each test case,The first line contains three integers

The second line contains two numbers

Then

Note. There may be multiple edges between two vertices.

Output

One line containing a sentence. Begin with the case number. If it is possible to pick some edges to make the graph fantastic, output "Yes" (without quote), else output "No" (without quote).

样例输入

样例输出

Case 1: Yes
Case 2: No

题目来源

ACM-ICPC 2018 沈阳赛区网络预赛

题目大意：给出一个二分图，再给出一些边，再给出L，R，从这些边中选取一些使得每一个点的度都在[L,R]之间。

题目思路：建立超级源点S，连接二分图左边的所有点，流量下界L,上界为R，同理将右半边所有点连接到超级汇点T。

将给出的边连接，流量下界0,上界为1。然后套个有上下界的网络流板子判断是否有解就行了。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int LEN = 1e5 + 5;
const int oo = (1LL << 31) - 1;
namespace DINIC {
int tot, src, tar, qh, qt, cnt, s, t, S, T;
int ans, flow;
struct edge {
    int vet, next, len;
} E[LEN * 2];
int dis[LEN], head[LEN], cur[LEN], q[LEN], IN[LEN];
void add(int u, int v, int c) {
    E[++tot] = (edge) {
        v, head[u], c
    };
    head[u] = tot;
}
void join(int u, int v, int c) {
    add(u, v, c);
    add(v, u, 0);
}
void init() {
    tot = -1;
    for (int i = 1; i <= cnt + 2; i++)
        head[i] = -1;
}
bool bfs() {
    memset(dis, 0, sizeof(dis));
    qh = qt = 0;
    q[++qt] = src;
    dis[src] = 1;
    while (qh < qt) {
        int u = q[++qh];
        for (int e = head[u]; e != -1; e = E[e].next) {
            int v = E[e].vet;
            if (E[e].len && !dis[v]) {
                dis[v] = dis[u] + 1;
                if (v == tar)
                    return 1;
                q[++qt] = v;
            }
        }
    }
    return dis[tar];
}
int dfs(int u, int aug) {
    if (u == tar || !aug)
        return aug;
    int tmp = 0;
    for (int &e = cur[u]; e != -1; e = E[e].next) {
        int v = E[e].vet;
        if (dis[v] == dis[u] + 1) {
            if (tmp = dfs(v, min(aug, E[e].len))) {
                E[e].len -= tmp;
                E[e ^ 1].len += tmp;
                return tmp;
            }
        }
    }
    return 0;
}
int maxflow(int s, int t) {
    src = s, tar = t;
    int res = 0, flow = 0;
    while (bfs()) {
        for (int i = 1; i <= cnt + 2; i++)
            cur[i] = head[i];
        while (flow = dfs(src, oo))
            res += flow;
    }
    return res;
}
}
using namespace DINIC;

int N, M, K, L, R;

int main() {
    int cas = 1;
    while(~scanf("%d %d %d", &N, &M, &K)) {
        scanf("%d %d", &L, &R);
        memset(IN, 0, sizeof(IN));
        ans = flow = 0;
        cnt = N + M + 2;
        s = N + M + 1;
        t = N + M + 2;
        S = ++cnt, T = ++cnt;
        init();
        for(int i = 1; i <= K; i++ ) {
            int u, v, l = 0, r = 1;
            scanf("%d %d", &u, &v);
            join(u, v + N, r - l);
            IN[v] += l, IN[u] -= l;
        }
        for(int i = 1; i <= N; i++ ) {
            int u, v, l = L, r = R;
            u = s, v = i;
            join(u, v, r - l);
            IN[v] += l, IN[u] -= l;
        }
        for(int i = 1; i <= M; i++ ) {
            int u, v, l = L, r = R;
            u = i + N, v = t;
            join(u, v, r - l);
            IN[v] += l, IN[u] -= l;
        }

        for (int i = 1; i <= N + M + 2; i++) {
            if (IN[i] < 0) {
                join(i, T, -IN[i]);
            } else if (IN[i] > 0) {
                flow += IN[i];
                join(S, i, IN[i]);
            }
        }
        join(t, s, oo);
        ans = maxflow(S, T);
        printf("Case %d: ", cas++);
        if (ans != flow)
            puts("No");
        else {
//            ans = maxflow(s, t);
//            printf("%lld
", ans);
            puts("Yes");
        }
    }
    return 0;
}

View Code

G.Spare Tire

A sequence of integer $a_n brace{an} can be expressed as:$

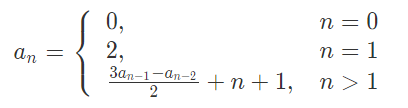
Now there are two integers

But I have no time to solve this problem because I am going to date my boyfriend soon. So can you help me?

Input

Input contains multiple test cases ( about $mm.1≤n,m≤10^8.$

Output

For each test case, print the answer of my question(after mod

Hint

In the all integers from

样例输入

4 4

样例输出

题目来源

ACM-ICPC 2018 沈阳赛区网络预赛

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int vis[10005],pri[10005],top;
int a[10005],h;
ll n,m,ans,sum;
ll p1,p2;
void init()
{
    top=0;
    for(int i=2; i<10005; i++)
    {
        if(!vis[i])
        {
            pri[++top]=i;
            for(int j=i+i; j<10005; j+=i)
                vis[j]=1;
        }
    }
}
ll qpow(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1)
            ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
}
ll getsum(int x)
{
    if(!x||x==1)
        return 0;
    int i,j,k;
    ll ans;
    k=n/x;
    ans=1LL*k*(k+1)%mod*p1%mod*x%mod;
    ans+=(1LL*k*(k+1)%mod*(2*k+1)%mod*p2%mod*x%mod*x%mod);
    ans=ans%mod;
    return ans;
}
void dfs(int i,int num,int x)
{
    if(x>n)
        return ;
    if(i==h)
    {
        if(num%2)
        {
            sum+=getsum(x);
            sum=sum%mod;
        }
        else
            sum-=getsum(x);
        return ;
    }
    dfs(i+1,num+1,x*a[i]);
    dfs(i+1,num,x);


}
int main()
{
    int i,j,k,t,cas;
    ll w;
    init();
    p1=qpow(2,mod-2);
    p2=qpow(6,mod-2);
    while(scanf("%lld%lld",&n,&m)!=EOF)
    {
        ans=1LL*n*(n+1)%mod*p1%mod;
        ans+=(1LL*n*(n+1)%mod*(2*n+1)%mod*p2%mod);
        ans=ans%mod;
        h=0;
        w=m;
        for(i=1; i<=top; i++)
        {
            if(w%pri[i]==0)
            {
                a[h++]=pri[i];
                while(w%pri[i]==0)
                    w=w/pri[i];
            }
        }
        if(w!=1)
            a[h++]=w;
        sum=0;
        dfs(0,0,1);
        ans=(ans+mod-sum)%mod;
        printf("%lld
",ans);
    }
    return 0;
}

View Code

I.Lattice's basics in digital electronics

LATTICE is learning Digital Electronic Technology. He is talented, so he understood all those pieces of knowledge in $10^{-9}10−9 second. In the next 10^{-9}10−9 second, he built a data decoding device that decodes data encoded with his special binary coding rule to meaningful words.$

His coding rule is called "prefix code", a type of code system (typically a variable-length code) distinguished by its possession of the "prefix property", which requires that there is no whole code word in the system that is a prefix (initial segment) of any other code word in the system. Note that his code is composed of only

LATTICE's device only receives data that perfectly matches LATTICE's rules, in other words, people who send message to LATTICE will always obey his coding rule. However, in the process of receiving data, there are errors that cannot avoid, so LATTICE uses parity check to detect error bytes, after every

For example, consider the given data "101010101010101010101010", it should be divided into

Data passed the parity check will go into a process that decodes LATTICE's code. The process is described in the following example: consider a situation that, "010" represents 'A' and "1011" represents 'B', if the data after parity check is "01010110101011010010", it can be divided into "010"+"1011"+"010"+"1011"+"010"+"010", which means "ABABAA" . LATTICE's device is so exquisite that it can decode all visible characters in the ASCII table .

LATTICE is famous for his Talk show, some reporters have sneaked into his mansion, they stole the data LATTICE to decode in hexadecimal, the coding rule consists of

Input

The first line an integer

Every test case starts with one line containing two integers, $S_iSi is prefix of S_jSj.$

Then one line contains data that is going to be received in hexadecimal.

Output

For each test case, output the decoded message in a new line, the length of the decoded message should be the same with the length of original characters, which means you can stop decoding having outputted

样例输入

2
15 9
32 0100
33 11
100 1011
101 0110
104 1010
108 00
111 100
114 0111
119 0101
A6Fd021171c562Fde1
8 3
49 0001
50 01001
51 011
14DB24722698

样例输出

hello world!!!!
12332132

题目来源

ACM-ICPC 2018 沈阳赛区网络预赛

题目大意：

给出二进制和ASCLL码的对映规则，再给出一个16进制的字符串。将16进制的字符串转二进制，然后每九位校验一下（前八位中1的个数是奇数且第九位为1 或前八位中1的个数是偶数且第九位为0 则正确）

将正确的留下，再用题目给的规则转换成字符，只要前m个。暴力模拟下即可。

#include<cstdio>
#include<cstring>
using namespace std;

struct Trie
{
    int num;
    int next[2];
} tree[10000];
int cnt = 0;
char ttr[200050];
char ltr[800050];
bool a[800050];
int top = 0;

void getBit()
{
    int len = strlen(ttr);
    top = 0;
    for(int i=0; i<len; i++)
    {
        switch (ttr[i])
        {
        case '0':
            ltr[top]='0',ltr[top+1]='0',ltr[top+2]='0',ltr[top+3]='0',top+=4;
            break;
        case '1':
            ltr[top]='0',ltr[top+1]='0',ltr[top+2]='0',ltr[top+3]='1',top+=4;
            break;
        case '2':
            ltr[top]='0',ltr[top+1]='0',ltr[top+2]='1',ltr[top+3]='0',top+=4;
            break;
        case '3':
            ltr[top]='0',ltr[top+1]='0',ltr[top+2]='1',ltr[top+3]='1',top+=4;
            break;
        case '4':
            ltr[top]='0',ltr[top+1]='1',ltr[top+2]='0',ltr[top+3]='0',top+=4;
            break;
        case '5':
            ltr[top]='0',ltr[top+1]='1',ltr[top+2]='0',ltr[top+3]='1',top+=4;
            break;
        case '6':
            ltr[top]='0',ltr[top+1]='1',ltr[top+2]='1',ltr[top+3]='0',top+=4;
            break;
        case '7':
            ltr[top]='0',ltr[top+1]='1',ltr[top+2]='1',ltr[top+3]='1',top+=4;
            break;
        case '8':
            ltr[top]='1',ltr[top+1]='0',ltr[top+2]='0',ltr[top+3]='0',top+=4;
            break;
        case '9':
            ltr[top]='1',ltr[top+1]='0',ltr[top+2]='0',ltr[top+3]='1',top+=4;
            break;
        case 'a':
        case 'A':
            ltr[top]='1',ltr[top+1]='0',ltr[top+2]='1',ltr[top+3]='0',top+=4;
            break;
        case 'b':
        case 'B':
            ltr[top]='1',ltr[top+1]='0',ltr[top+2]='1',ltr[top+3]='1',top+=4;
            break;
        case 'c':
        case 'C':
            ltr[top]='1',ltr[top+1]='1',ltr[top+2]='0',ltr[top+3]='0',top+=4;
            break;
        case 'd':
        case 'D':
            ltr[top]='1',ltr[top+1]='1',ltr[top+2]='0',ltr[top+3]='1',top+=4;
            break;
        case 'e':
        case 'E':
            ltr[top]='1',ltr[top+1]='1',ltr[top+2]='1',ltr[top+3]='0',top+=4;
            break;
        case 'f':
        case 'F':
            ltr[top]='1',ltr[top+1]='1',ltr[top+2]='1',ltr[top+3]='1',top+=4;
            break;
        }
    }
    ltr[top]='';
}

void insert_tree(char str[],int num)
{
    int p = 0;
    int len = strlen(str);
    for(int i=0; i<len; i++)
    {
        if(tree[p].next[str[i]-'0'])
        {
            p = tree[p].next[str[i]-'0'];
        }
        else
        {
            tree[p].next[str[i]-'0'] = ++cnt;
            p = tree[p].next[str[i]-'0'];
        }
    }
    tree[p].num = num;
}

void solve()
{
    cnt = 0;
    int tot = 0;
    memset(tree,0,sizeof(tree));
    memset(a,0,sizeof(a));
    memset(ttr,0,sizeof(ttr));
    memset(ltr,0,sizeof(ltr));
    int m,n,num;
    char str[15];
    scanf("%d%d",&m,&n);
    while(n--)
    {
        scanf("%d%s",&num,str);
        insert_tree(str,num);
    }
    scanf("%s",ttr);
    getBit();

    for(int i=0; i<top; i+=9)
    {
        int cc=0;
        if(i+9>top)continue;
        for(int j=i; j<i+8; j++)
        {
            if(ltr[j]=='1')
                cc++;
        }
        if((cc%2==0&&ltr[i+8]=='1')||(cc%2==1&&ltr[i+8]=='0'))
        {
            for(int j=i; j<i+8; j++)
            {
                a[tot++] = ltr[j]-'0';
            }
        }
    }
    int root = 0;
    for(int i=0;i<tot;i++)
    {
        root = tree[root].next[a[i]];
        if(tree[root].num)
        {
            printf("%c",tree[root].num);
            m--;
            root = 0;
        }
        if(!m)break;
    }
    puts("");
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        solve();
    }
    return 0;
}

View Code

K.Supreme Number

A prime number (or a prime) is a natural number greater than

Now lets define a number

For example,

Now you are given an integer $(2≤N≤10^100), could you find the maximal supreme number that does not exceed NN?$

Input

In the first line, there is an integer

In the following $(2≤N≤10^100).$

Output

For each test case print "Case #x: y", in which

样例输入

2
6
100

样例输出

Case #1: 5
Case #2: 73

题目来源

ACM-ICPC 2018 沈阳赛区网络预赛

题意：找一个小于n的超级质数（其子序列也是质数），搜索。

#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int a[100005],top=0;
int b[]= {1,2,3,5,7},c[1005],d[1005];
int vis[100005];
int l,f;
void init()
{
    for(int i=2; i<100005; i++)
        if(!vis[i])
            for(int j=i+i; j<100005; j+=i)
                vis[j]=1;
}
void dfs1(int len,int x)
{
    if(len==l)
    {
        if(vis[x])
            f=0;
        return ;
    }
    dfs1(len+1,x*10+c[len]);
    dfs1(len+1,x);

}
int check(int x)
{
    f=1;
    l=0;
    while(x)
    {
        d[l++]=x%10;
        x=x/10;
    }
    for(int i=0; i<l; i++)
        c[i]=d[l-i-1];
    dfs1(0,0);
    return f;
}
void dfs(int len,int x)
{
    if(check(x)&&x)
        a[++top]=x;
    if(len==5)
    {
        return ;
    }
    for(int i=0; i<5; i++)
        dfs(len+1,x*10+b[i]);
}
int main()
{
    int i,j,t,cas=0,len,mmax,ans;
    char s[1005];
    init();
    dfs(0,0);
    sort(a+1,a+top+1);
    scanf("%d",&t);
    while(t--)
    {
        ++cas;
        scanf("%s",&s);
        len=strlen(s);
        if(len>5)
            mmax=1000000;
        else
        {
            mmax=0;
            for(i=0; i<len; i++)
                mmax=mmax*10+(s[i]-'0');
        }
        //printf("%d
",mmax);
        for(i=1; i<=top; i++)
            if(a[i]<=mmax)
                ans=a[i];
        printf("Case #%d: %d
",cas,ans);

    }
    return 0;
}

View Code

相关阅读:
[BZOJ1657] [Usaco2006 Mar] Mooo 奶牛的歌声 (单调栈)
[BZOJ1016] [JSOI2008] 最小生成树计数 (Kruskal)
[BZOJ1015] [JSOI2008] 星球大战starwar (并查集)
[BZOJ1007] [HNOI2008] 水平可见直线 (凸包)
[BZOJ1061] [Noi2008] 志愿者招募 (费用流)
[BZOJ1051] [HAOI2006] 受欢迎的牛 (强联通分量)
BZOJ2299: [HAOI2011]向量
 BZOJ2783: [JLOI2012]树
 BZOJ3521: [Poi2014]Salad Bar
BZOJ2429: [HAOI2006]聪明的猴子
原文地址：https://www.cnblogs.com/xcantaloupe/p/9611117.html

最新文章
洛谷月赛礼物
 找环
 观光公交
 Mayan游戏
 关键路径
 洛谷10月月赛
 LOJ 6057
AGC023E
uoj Goodbye Dingyou Round 题解
 计算几何模板