这节课内容介绍了SVM的核心。
首先,既然SVM都可以转化为二次规划问题了,为啥还有有Dual啥的呢?原因如下:
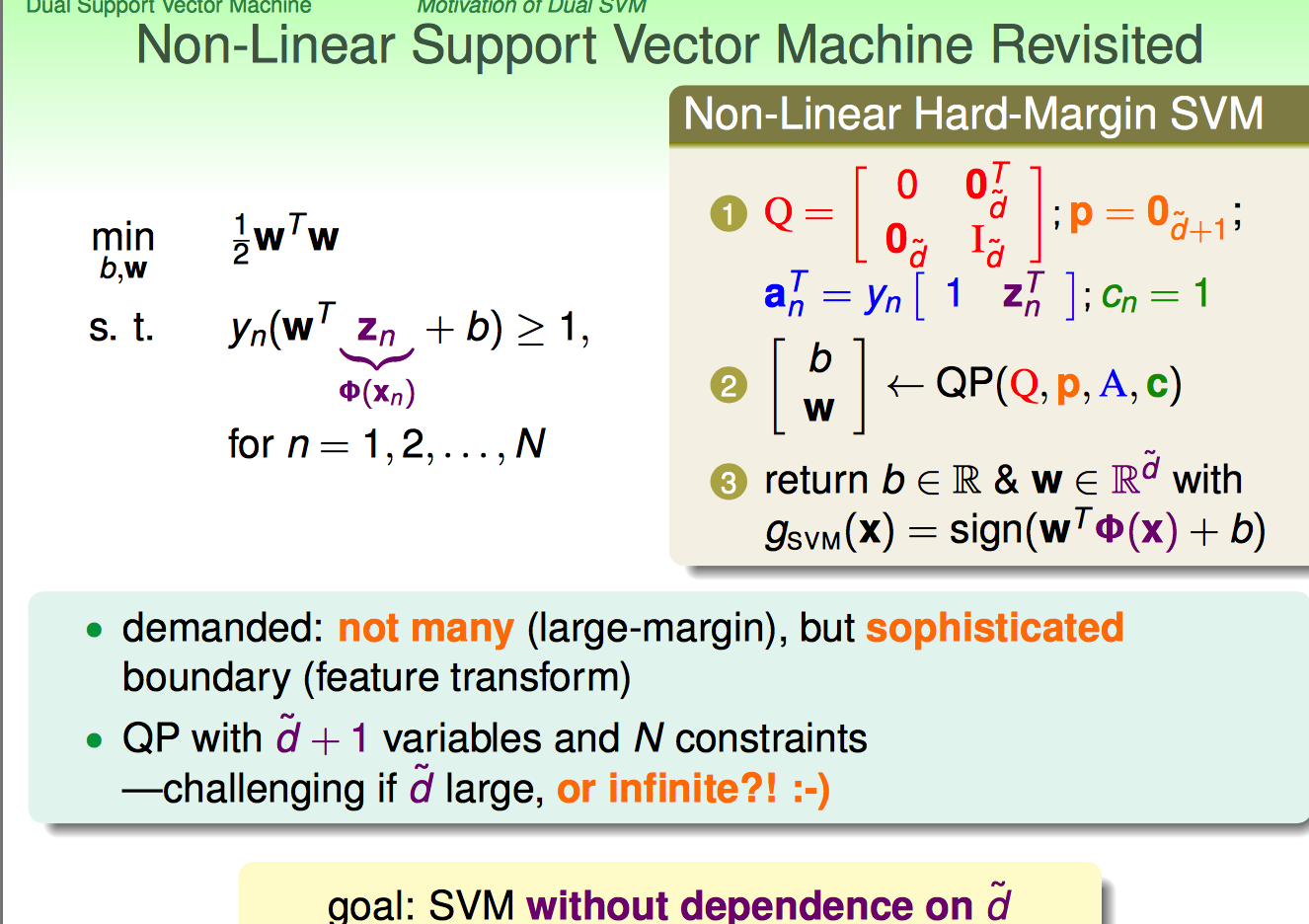
如果x进行non-linear transform后,二次规划算法需要面对的是d`+1维度的N个变量,以及N个约束
如果d`的维度超大,那么二次规划解起来的代价就太大了。因此,SVM的精髓就在于做了如下的问题转化:
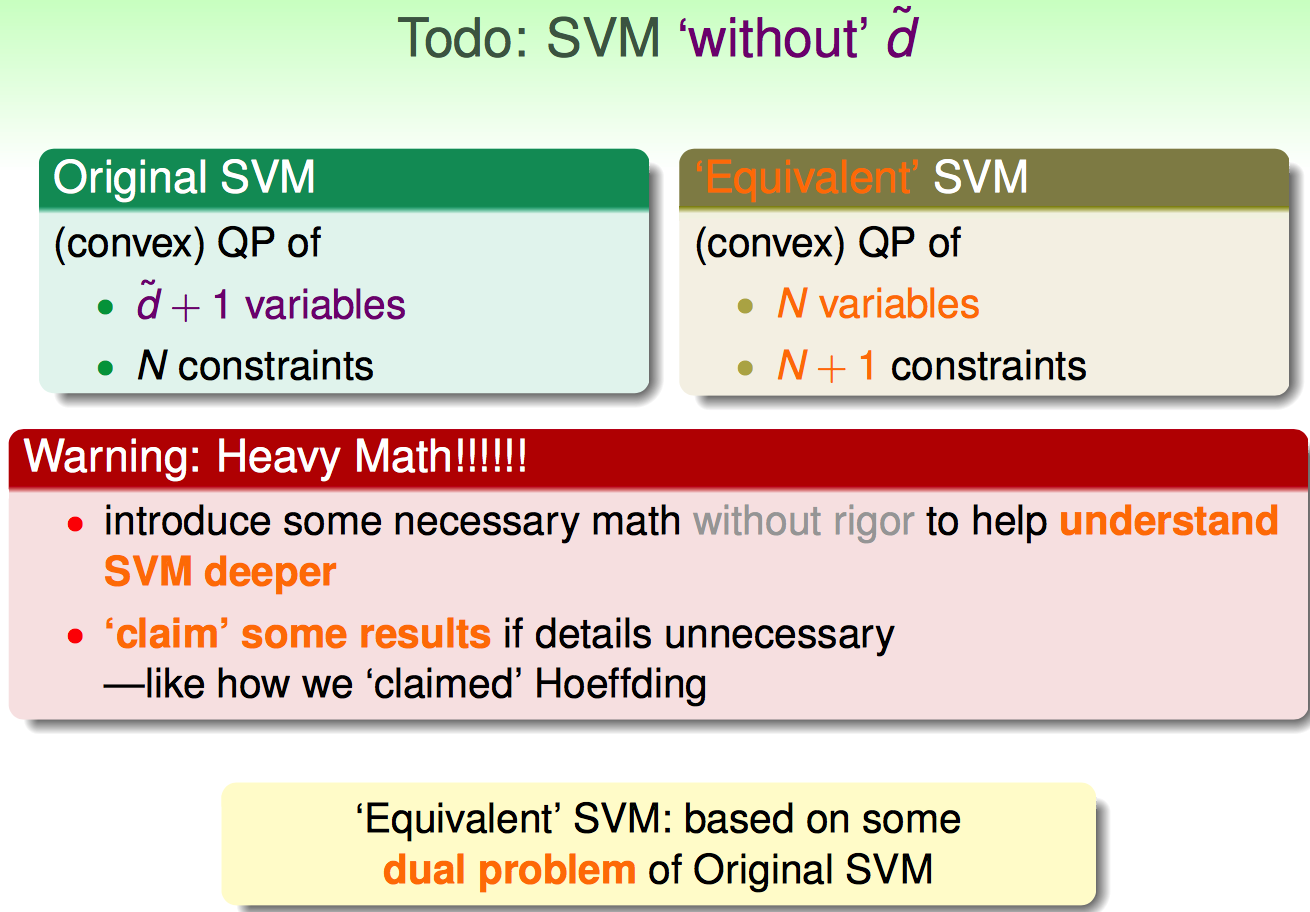
不需要问太深奥的数学,知道为啥要dual的motivation就可以了。
这里再次搬出前人的智慧:Lagrange Multipliers
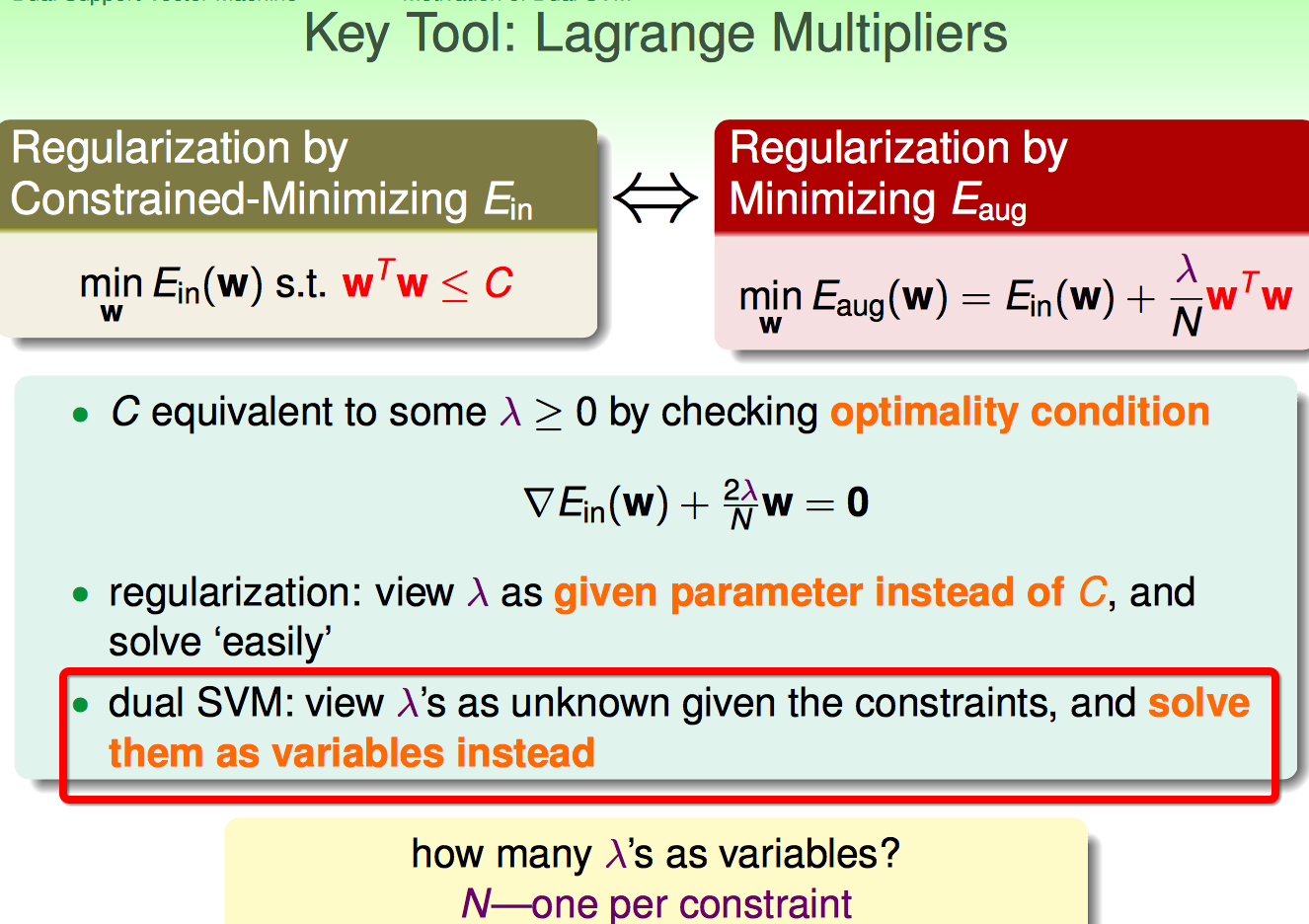
但是这里跟ridge regression不太一样:一个约束条件配一个拉格朗日乘子;每个乘子是未知的,需要求解的变量。

如上图,首先把原问题的N个不等式约束条件,通过拉格朗日乘子给弄到等式中。
问题困惑:原来的目标函数是min (b,W) 0.5W'W,而且还是min;为啥用Lagrange Fucntion转换后,还搞出来一个max呢?背后的原因是啥呢?
我的理解:这里max的目的是把违背约束条件的(b,W)的值无限放大
(1)违背约束条件:alpha后面的值是正数,那么max必然是alpha取无限大的情况;这样经过外层的min操作,必然过滤掉了
(2)符合约束条件:alpha后面的值是非正,那么max必然是alpha取零的情况;这样min里面剩下的项就是原目标函数了;
综合(1)(2)来看,拉格朗日乘子起到这样的作用:
a. 把不等式约束给弄到等式中
b. 把违背约束的项目给弄到无限大
c. 如果符合约束条件,等式中的拉格朗日项目就没有了;这样剩下的自然就是原来需要min的目标函数
综合b,c来看,拉格朗日乘子用一种特殊的方式把违背约束条件的(b,W)给排除了,把符合约束条件的(b,W)给留在了候选集合中。
这样转换后的问题就跟原问题等价了;约束条件藏在了max里面。
接下需要进一步转化:

交换min和max的顺序:
(1)原来的max里面(b,W)是受到约束条件限制的
(2)交换min和max后,(b,W)可以不受到约束条件限制
转换后的问题,叫Lagrange dual problem。
光大于等于还不行,最好能等于:

要想是强对偶问题,QP需要满足:
(1)原问题是convex的
(2)原问题是feasible的(即线性可分)
(3)约束条件是线性的
于是,就可以放心大胆地取等号了。
分别对b和W求导,获得梯度为零的条件。

通过梯度为0的条件,把min里的b和W都替换掉了;由于min的变量是(b,W),但现在变量只剩下alpha了,所以min也可以直接去掉了。
这里涉及到一些矩阵微分的内容(http://blog.sciencenet.cn/blog-849193-653656.html)
关于b的梯度求解很直观。
关于W的梯度求解,可以转化成矩阵向量表示。
(1)二次项求导的结果就是W
(2)一次项求导可以做如下的变换,以及最终的表达式如下。

这样W就完全用y,z,alpha表示出来了;另外,从这可以看出来W其实是输入向量Z的线性组合,每个Zn前面的系数就是alphan yn。
以上一系列转化的背后是KKT条件。

有了KKT条件,只要求出来最优的alpha就相当于间接求出来了(b,W).
KKT里面后两个条件比较重要:
(1)dual problem的inner部分要满足梯度为0(即取得最优化的值)
(2)原问题取得最优化值的同时,其中的拉格朗日乘子必须disappear

最终,转化为对偶问题后的最优化问题,就保持了N个变量(alpha),N+1个约束条件。对比原问题,变量的维度控制在了1(原来的维度是d`+1)。
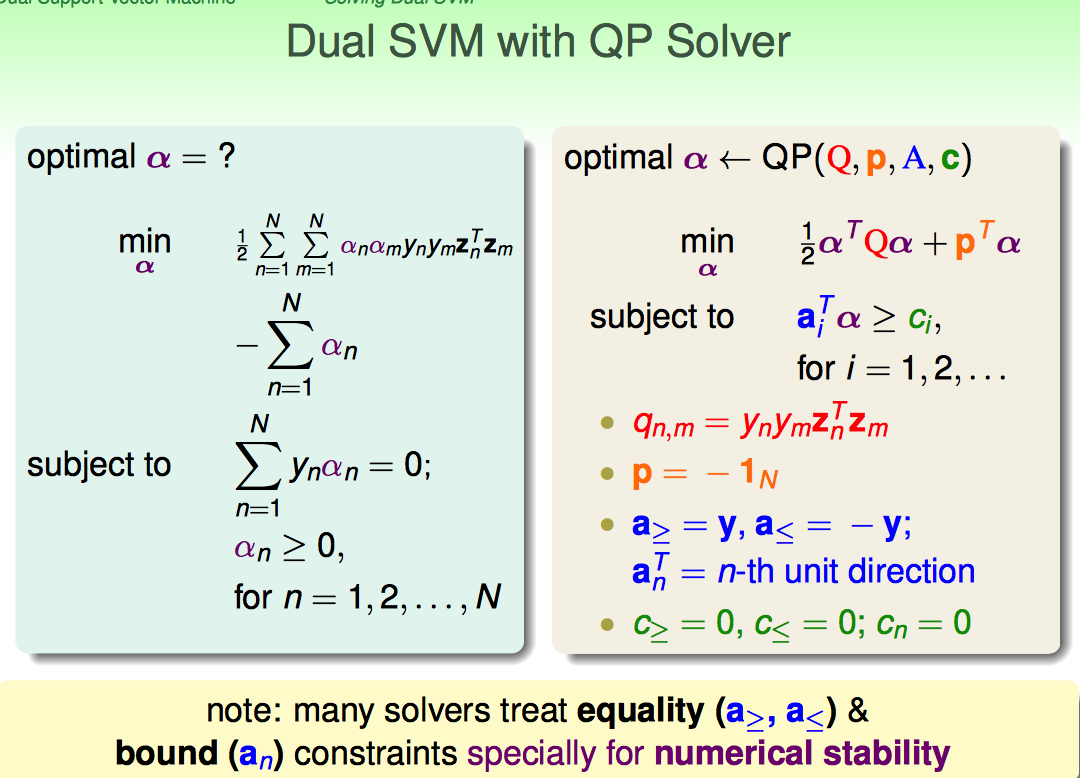
直接套用QP Solver即可
目标函数:
(1)二次项系数qn,m = ynymZn'Zm
(2)一次项系数-IN
约束条件:
(1)等于0的情况可以用“大于等于∩小于等于”来代替
(2)对于alphan大于等0的情况,用n那个单位方向向量做系数([1,0.....] [0,1,0,....], .... , [0,....,0,1])

这里提到了一个东西:输入变量d`+1维度的代价哪去了?其实,转化到了qn,m中去了。
其实到这里,还是对为何要转成dual problem不十分确定,只能说是计算的代价发生了变化。
转化后约束条件的系数变得简单了,但是样本维度N一般都会大于输入维度d'很多啊,相当于目标函数复杂了一些。这样计算代价真的降低了么?
估计要想明白这个问题,还得看看QP问题是怎么求解的,后续再看吧。
总之,这里的Q矩阵依然是个N×N的矩阵,如果N很大占用的内存非常多,因此需要把特殊的求解工具才能搞定。

前面一大堆推导,后面的结论就是:
(1)最后只有alpha大于0的点被成为支撑向量(SV)
(2)最终W由所有支撑向量决定
(3)任意一个支撑向量都可以算出来b

这里回顾了之前讲过线性分类模型:W都可以看成输入数据的线性组合;SVM之所以好,是因为W只用支撑向量的线性组合就可以表示了。

这里留了一个问题:如果输入数据经过比较复杂的tranform了,还是比较难搞的,怎么能让算法摆脱d'的限制?