现在的题都好难啊
看题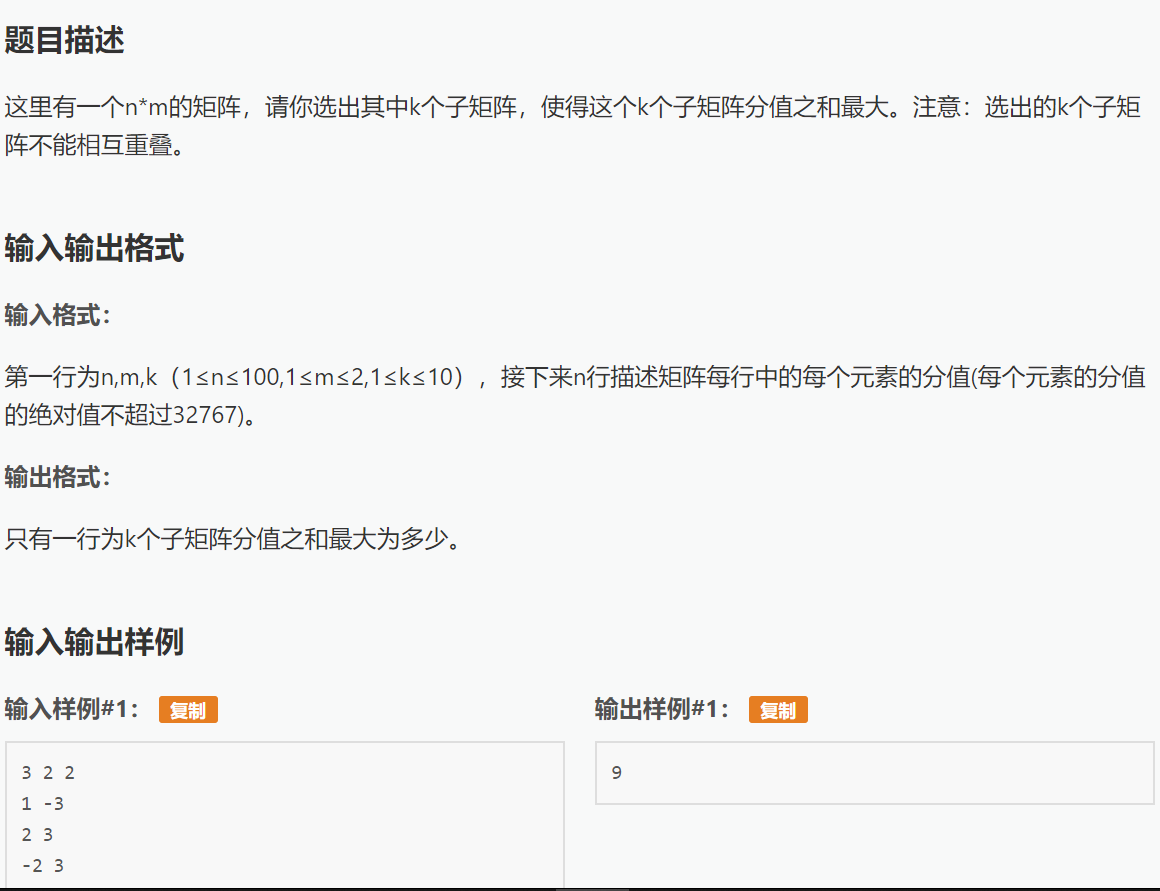
这道题我一开始觉得很简单写了一个小时,发现自己写了一个错的算法
于是看了看题解
发现并没有这么简单
我来讲解一下
看到了m的范围
1<=m<=2
如果m=1,这题就很简单了,就是求k个最大子段和
这里可以分开来讨论
m=1时的dp方程就是
dp[i][j][1]=max(dp[i-1][j-1][0],dp[i-1][j][1])+x;
dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]);
最后取两个max
如果m=2时怎么办呢?
设dp[i][j][0~4],表示到了i,j位置,0~4操作能获得的最大值
0操作是当前这一排什么都不取
1操作是当前这一排取左边的一块,空出了右边
2操作是当前这一排取右边的一块,空出了左边
3操作是当前这一排的左右,但是左右两列分别成块
4操作是取当前这一排,左右都成为一块
接下来是dp的转移
dp[i][j][0]=max(max(dp[i-1][j][0],dp[i-1][j][1]),max(dp[i-1][j][2],dp[i-1][j][3]));
dp[i][j][0]=max(dp[i][j][0],dp[i-1][j][4]);
当前是0,则是承接上一个状态的最大值
dp[i][j][1]=max(max(dp[i-1][j-1][0],dp[i-1][j][1]),max(dp[i-1][j-1][2],dp[i-1][j][3]))+x;
dp[i][j][1]=max(dp[i][j][1],dp[i-1][j-1][4]+x);
当前是1,则可以合并上一个状态的操作1,和操作3,再取所有操作的最大值,最后加上当前位置的值
dp[i][j][2]=max(max(dp[i-1][j-1][0],dp[i-1][j-1][1]),max(dp[i-1][j][2],dp[i-1][j][3]))+y;
dp[i][j][2]=max(dp[i][j][2],dp[i-1][j-1][4]+y);
当前是2,则可以合并上一个状态的操作2,和操作3,再取所有操作的最大值,最后加上当前位置的值
dp[i][j][3]=max(dp[i-1][j-1][1],max(dp[i-1][j-1][2],dp[i-1][j][3]))+x+y;
if(j>=2)
dp[i][j][3]=max(dp[i][j][3],dp[i-1][j-2][4]+x+y);
当前是3,则可以合并合并上一个状态的3,左边和右边取一个max,在加上max位置的值
dp[i][j][4]=max(max(dp[i-1][j-1][0],dp[i-1][j-1][1]),max(dp[i-1][j-1][2],dp[i-1][j-1][3]))+x+y;
dp[i][j][4]=max(dp[i][j][4],dp[i-1][j][4]+x+y);
当前是4,则只能合并上一个状态的4,在与所有的取max,在加上这一排的数
最后所有的操作取max
贴上我的代码
1 #include <cstdio> 2 #include <cstdlib> 3 #include <iostream> 4 #include <algorithm> 5 #include <cstring> 6 using namespace std; 7 const int N=105; 8 int dp[N][N][10],x,y,n,m,K; 9 int main() 10 { 11 scanf("%d %d %d",&n,&m,&K); 12 if(m==1) 13 { 14 for(int i=1;i<=n;i++) 15 { 16 scanf("%d",&x); 17 for(int j=1;j<=K;j++) 18 { 19 dp[i][j][1]=max(dp[i-1][j-1][0],dp[i-1][j][1])+x; 20 dp[i][j][0]=max(dp[i-1][j][0],dp[i-1][j][1]); 21 22 } 23 } 24 printf("%d ",max(dp[n][K][0],dp[n][K][1])); 25 return 0; 26 } 27 else 28 { 29 memset(dp,-0x3f,sizeof(dp)); 30 for(int i=0;i<=n;i++) 31 for(int j=0;j<=K;j++) 32 dp[i][j][0]=0; 33 for(int i=1;i<=n;i++) 34 { 35 scanf("%d %d",&x,&y); 36 for(int j=1;j<=K;j++) 37 { 38 dp[i][j][0]=max(max(dp[i-1][j][0],dp[i-1][j][1]),max(dp[i-1][j][2],dp[i-1][j][3])); 39 dp[i][j][0]=max(dp[i][j][0],dp[i-1][j][4]); 40 41 42 dp[i][j][1]=max(max(dp[i-1][j-1][0],dp[i-1][j][1]),max(dp[i-1][j-1][2],dp[i-1][j][3]))+x; 43 dp[i][j][1]=max(dp[i][j][1],dp[i-1][j-1][4]+x); 44 45 46 dp[i][j][2]=max(max(dp[i-1][j-1][0],dp[i-1][j-1][1]),max(dp[i-1][j][2],dp[i-1][j][3]))+y; 47 dp[i][j][2]=max(dp[i][j][2],dp[i-1][j-1][4]+y); 48 49 dp[i][j][3]=max(dp[i-1][j-1][1],max(dp[i-1][j-1][2],dp[i-1][j][3]))+x+y; 50 if(j>=2) 51 dp[i][j][3]=max(dp[i][j][3],dp[i-1][j-2][4]+x+y); 52 53 54 dp[i][j][4]=max(max(dp[i-1][j-1][0],dp[i-1][j-1][1]),max(dp[i-1][j-1][2],dp[i-1][j-1][3]))+x+y; 55 dp[i][j][4]=max(dp[i][j][4],dp[i-1][j][4]+x+y); 56 } 57 } 58 int ans=max(max(dp[n][K][0],dp[n][K][1]),max(dp[n][K][2],dp[n][K][3])); 59 ans=max(ans,dp[n][K][4]); 60 printf("%d ",ans); 61 } 62 return 0; 63 }