题目传送门(内部题67)
输入格式
第一行,三个整数$n$、$k$、$p$。
第二行,$n$个自然数,表示${a_i}$。
输出格式
输出一行,两个自然数,表示$f(res)$、$res$。
样例
样例输入1:
4 3 5
2 0 3 7
样例输出1:
4 4
样例输入2:
2 2 1
2 0
样例输出2:
0 2
数据范围与提示
本题有$spj$,输出格式正确的情况下,仅回答正确$f(res)$、$res$中的一个可以获得$60\%$的分数(向下取整)。
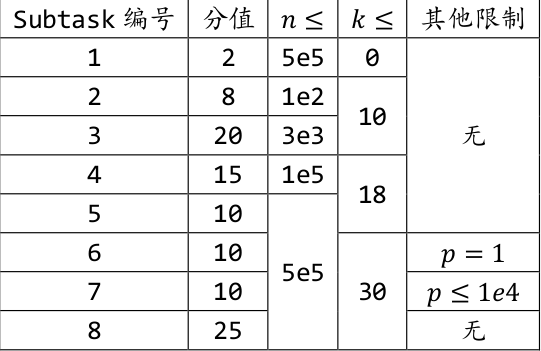
题解
考虑怎样才能形成逆序对,或怎样才能让本身的逆序对消失。
设$a,b$,将其分解为二进制,我们只有改变其最高的不同位才能改变其大小关系;若对于其最高的不同位$a$为$0$,$b$为$1$,那么如果$xor$一个这一位是$1$的数,则其大小关系会改变,反之同理。
所以考虑$Trie$,将每一个$a_i$分解成二进制插入并计算贡献即可。
这样的算法是$55$分的。
考虑如何优化,部分正确提示了可以二分。
二分逆序对的个数即可,最后再用二分出来的值返回去找$res$即可。
时间复杂度:$Theta(log n^2 imes 2^{frac{k}{2}})$。
期望得分:$100$分。
实际得分:$100$分。
代码时刻
#include<bits/stdc++.h>
using namespace std;
int k;
long long n,p;
int trie[20000000][2],cnt=1;
long long sum[20000000][2],num[20000000];
long long ans;
long long val;
long long que[3000001];
pair<long long,int> f1[3000001],f2[3000001];
void insert(int x)
{
int p=0;
for(int i=k-1;i>=0;i--)
{
if(!trie[p][(x>>i)&1])trie[p][(x>>i)&1]=++cnt;
sum[i][(x>>i)&1]+=num[trie[p][((x>>i)&1)^1]];
p=trie[p][(x>>i)&1];
num[p]++;
}
}
bool judge(long long x)
{
long long res=0;
int fail=(1<<(k-k/2));
for(int i=0;i<(1<<(k/2))&&f1[i].first<=x;i++)
{
while(x-f1[i].first<=f2[fail-1].first&&fail)fail--;
res+=fail;
}
if(res<p){val=res;return 1;}
return 0;
}
long long getans()
{
int fail=(1<<(k-k/2))-1;
for(int i=0;i<(1<<(k/2))&&f1[i].first<=ans;i++)
{
long long x=ans-f1[i].first;
while(x<f2[fail].first&&fail>=0)fail--;
if(f2[fail].first==x)que[++que[0]]=f1[i].second+(1<<(k/2))*f2[fail].second;
}
sort(que+1,que+que[0]+1);
return que[p-val];
}
int main()
{
scanf("%lld%d%lld",&n,&k,&p);
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
insert(x);
}
for(int i=0;i<(1<<(k/2));i++)
{
for(int j=0;j<(k/2);j++)f1[i].first+=sum[j][i>>j&1];
f1[i].second=i;
}
for(int i=0;i<(1<<(k-k/2));i++)
{
for(int j=0;j<(k-k/2);j++)f2[i].first+=sum[j+k/2][i>>j&1];
f2[i].second=i;
}
sort(f1,f1+(1<<(k/2)));
sort(f2,f2+(1<<(k-k/2)));
long long lft=0,rht=n*(n-1)/2;
while(lft<=rht)
{
long long mid=(lft+rht)>>1;
if(judge(mid)){lft=mid+1;ans=mid;}
else rht=mid-1;
}
printf("%lld %lld",ans,getans());
return 0;
}
rp++