7大排序

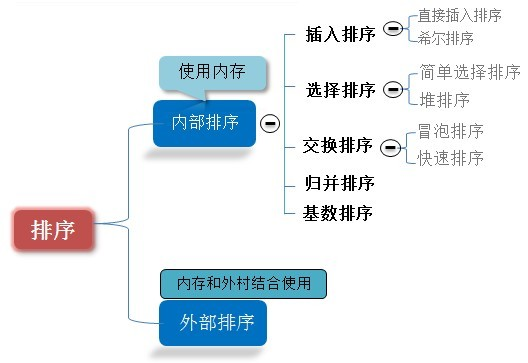
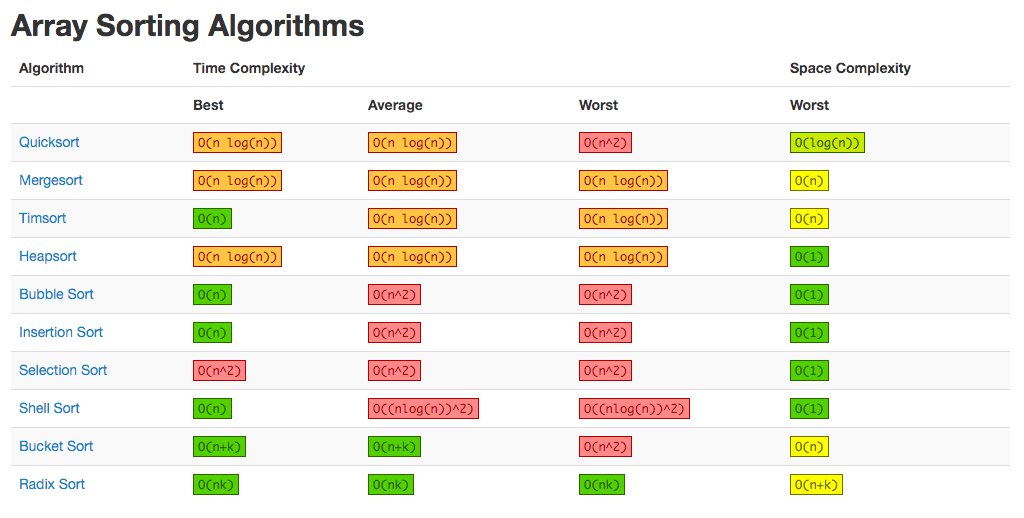
一、直接插入排序

往有序的数组中快速插入一个新的元素。

基本思想：将数组中的所有元素依次跟前面已经排好的元素相比较，如果选择的元素比已排序的元素小，则交换，直到全部元素都比较过为止。

// 插入排序
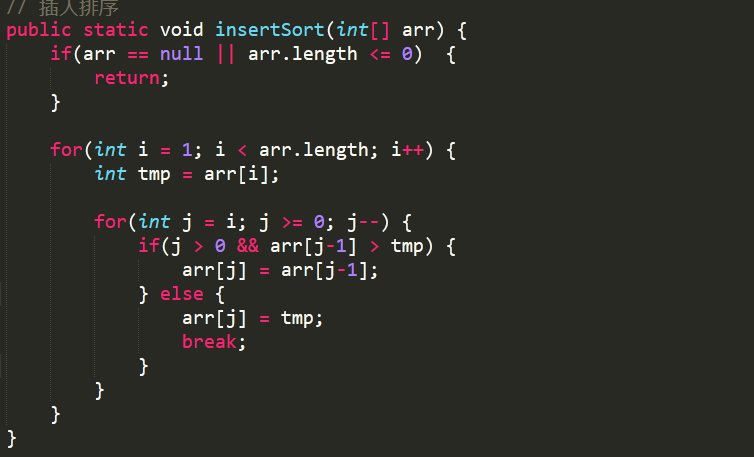
public static void insertSort(int[] arr) {
    if(arr == null || arr.length <= 0)  {
        return;
    }

    for(int i = 1; i < arr.length; i++) {
        int tmp = arr[i];
        
        for(int j = i; j >= 0; j--) {
            if(j > 0 && arr[j-1] > tmp) {
                arr[j] = arr[j-1];
            } else {
                arr[j] = tmp;
                break;
            }
        }
    }
}

 二、希尔排序

希尔排序又称递减增量排序算法。希尔排序是先把待排序的记录序列分割成若干子序列，分别进行直接插入排序，待整个序列中基本有序时，再对全体记录进行直接插入排序。

①. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；（一般初次取数组半长，之后每次再减半，直到增量为1）
②. 按增量序列个数k，对序列进行k 趟排序；
③. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

希尔排序实质上是一种分组插入方法。它的基本思想是：对于n个待排序的数列，取一个小于n的整数gap(gap被称为步长)将待排序元素分成若干个组子序列，所有距离为gap的倍数的记录放在同一个组中；然后，对各组内的元素进行直接插入排序。 这一趟排序完成之后，每一个组的元素都是有序的。然后减小gap的值，并重复执行上述的分组和排序。重复这样的操作，当gap=1时，整个数列就是有序的。

下面以数列{80,30,60,40,20,10,50,70}为例，演示它的希尔排序过程

第1趟：(gap=4)

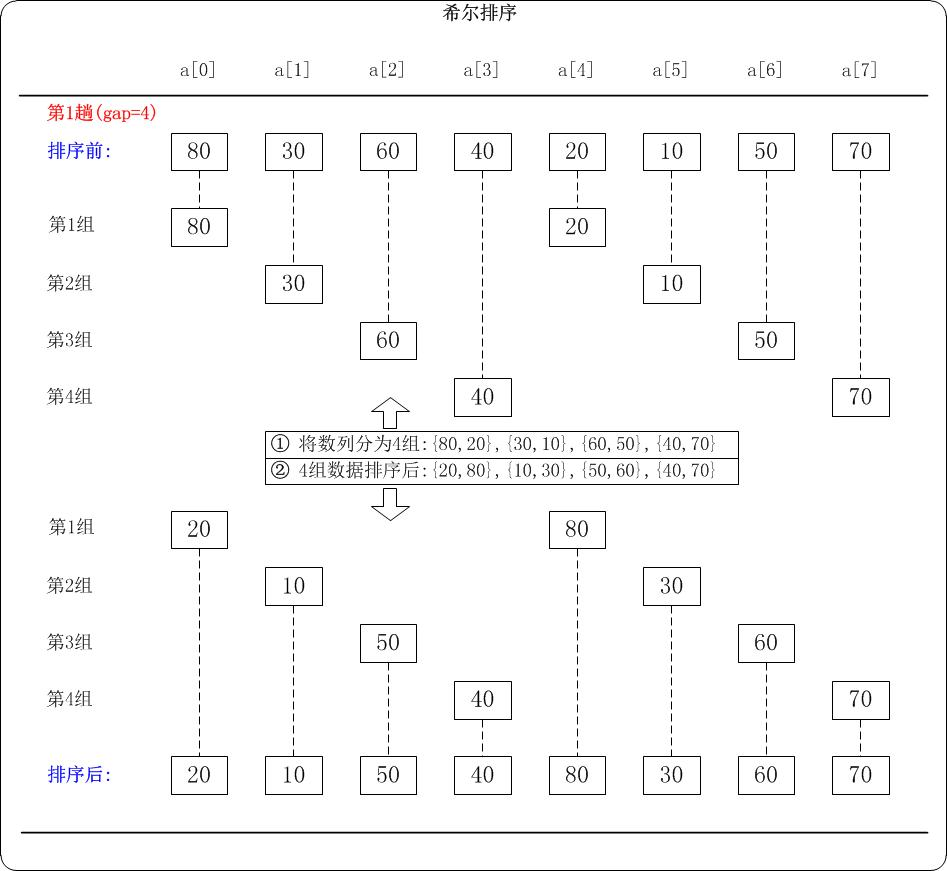
当gap=4时,意味着将数列分为4个组： {80,20},{30,10},{60,50},{40,70}。 对应数列： {80,30,60,40,20,10,50,70}
对这4个组分别进行排序，排序结果： {20,80},{10,30},{50,60},{40,70}。 对应数列： {20,10,50,40,80,30,60,70}

第2趟：(gap=2)

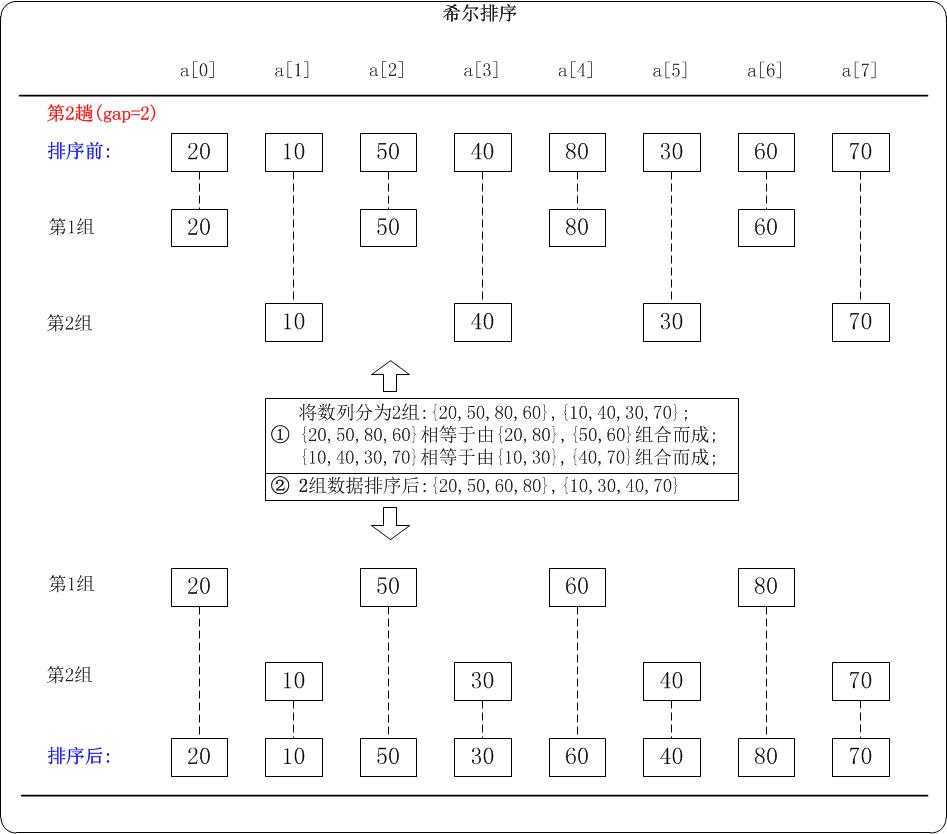
当gap=2时,意味着将数列分为2个组：{20,50,80,60}, {10,40,30,70}。 对应数列： {20,10,50,40,80,30,60,70}
注意：{20,50,80,60}实际上有两个有序的数列{20,80}和{50,60}组成。
          {10,40,30,70}实际上有两个有序的数列{10,30}和{40,70}组成。
对这2个组分别进行排序，排序结果：{20,50,60,80}, {10,30,40,70}。 对应数列： {20,10,50,30,60,40,80,70}

第3趟：(gap=1)

当gap=1时,意味着将数列分为1个组：{20,10,50,30,60,40,80,70}
注意：{20,10,50,30,60,40,80,70}实际上有两个有序的数列{20,50,60,80}和{10,30,40,70}组成。
对这1个组分别进行排序，排序结果：{10,20,30,40,50,60,70,80}

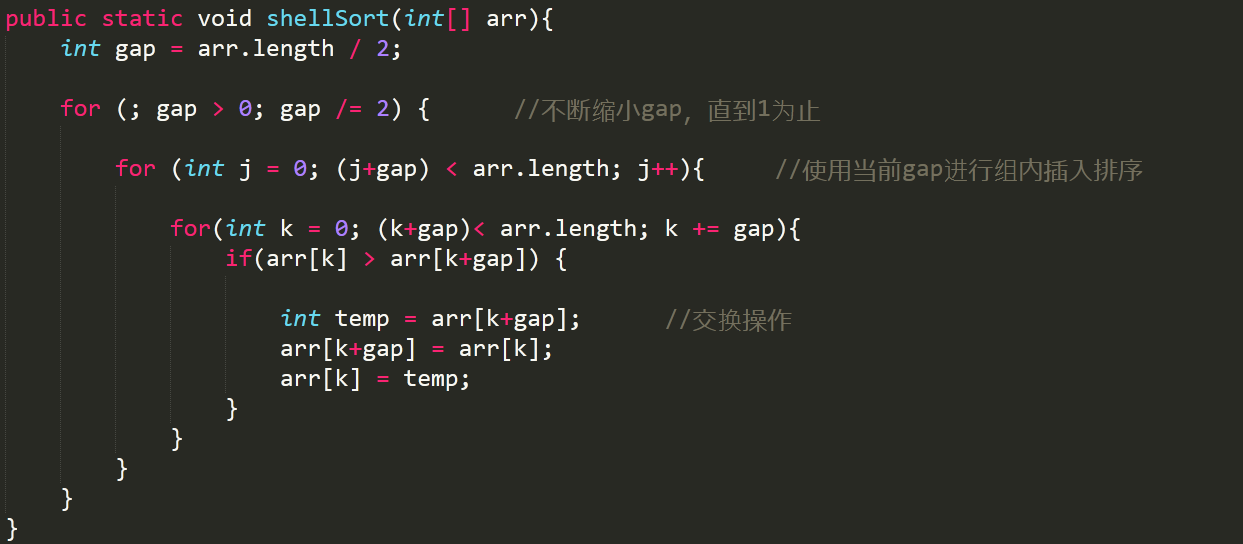
public static void shellSort(int[] arr){
    int gap = arr.length / 2;

    for (; gap > 0; gap /= 2) {      //不断缩小gap，直到1为止

        for (int j = 0; (j+gap) < arr.length; j++){     //使用当前gap进行组内插入排序

            for(int k = 0; (k+gap)< arr.length; k += gap){
                if(arr[k] > arr[k+gap]) {
                    
                    int temp = arr[k+gap];      //交换操作
                    arr[k+gap] = arr[k];
                    arr[k] = temp;
                }
            }
        }
    }
}

三、选择排序

选择排序的基本思想：比较+交换

①、从待排序的序列中，找到关键字最小的元素；

②、如果最小的元素不是待排序序列的第一个元素，将其和第一个元素交换；

③、从余下的N-1个元素中，找出关键字最小的元素，重复1和2，直到排序结束

// 选择排序
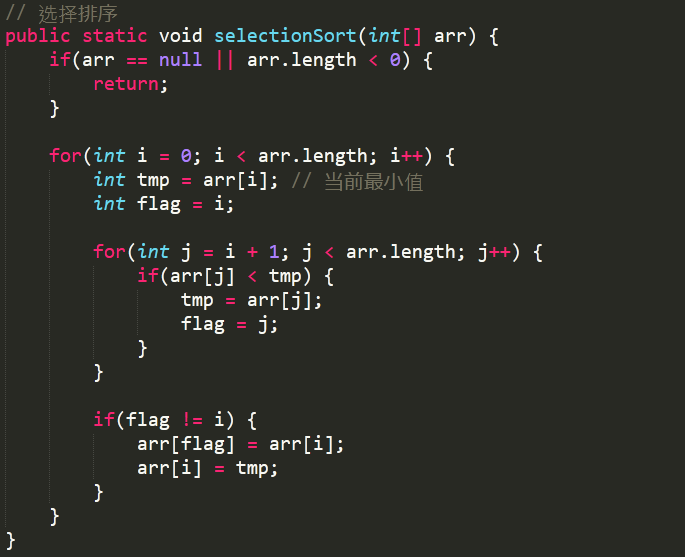
public static void selectionSort(int[] arr) {
    if(arr == null || arr.length < 0) {
        return;
    }

    for(int i = 0; i < arr.length; i++) {
        int tmp = arr[i]; // 当前最小值
        int flag = i;

        for(int j = i + 1; j < arr.length; j++) {
            if(arr[j] < tmp) {
                tmp = arr[j];
                flag = j;
            }
        }

        if(flag != i) {
            arr[flag] = arr[i];
            arr[i] = tmp;
        }
    }
}

四、堆排序

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

　　a.假设给定无序序列结构如下

2.此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

4.找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

此时，我们就将一个无需序列构造成了一个大顶堆。

步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

a.将堆顶元素9和末尾元素4进行交换

b.重新调整结构，使其继续满足堆定义

c.再将堆顶元素8与末尾元素5进行交换，得到第二大元素8.

后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

再简单总结下堆排序的基本思路：

　　a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

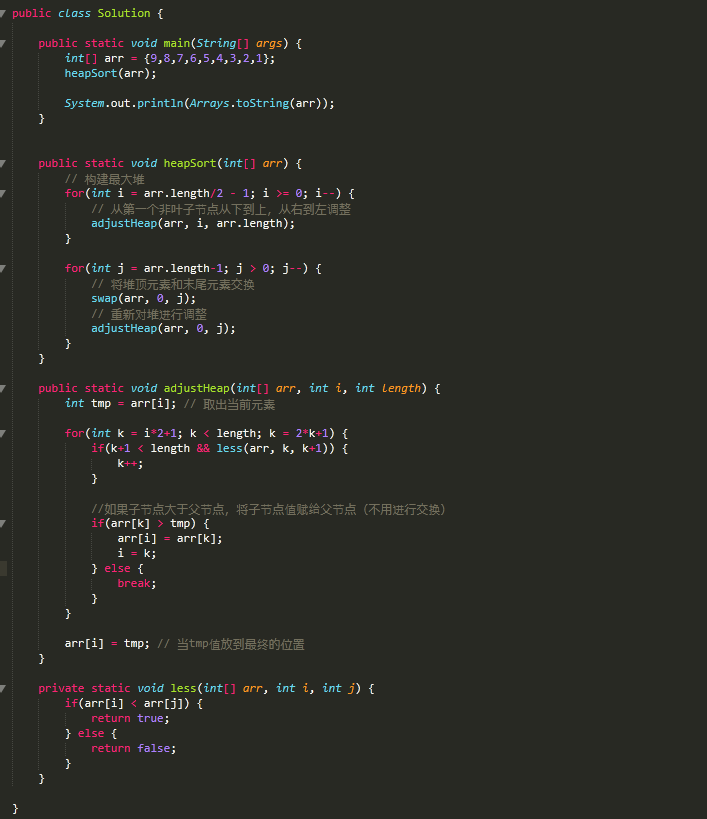
public class Solution {

    public static void main(String[] args) {
        int[] arr = {9,8,7,6,5,4,3,2,1};
        heapSort(arr);

        System.out.println(Arrays.toString(arr));
    }


    public static void heapSort(int[] arr) {
        // 构建最大堆
        for(int i = arr.length/2 - 1; i >= 0; i--) {
            // 从第一个非叶子节点从下到上，从右到左调整
            adjustHeap(arr, i, arr.length);
        }

        for(int j = arr.length-1; j > 0; j--) {
            // 将堆顶元素和末尾元素交换
            swap(arr, 0, j);
            // 重新对堆进行调整
            adjustHeap(arr, 0, j);
        }
    }

    public static void adjustHeap(int[] arr, int i, int length) {
        int tmp = arr[i]; // 取出当前元素
        
        for(int k = i*2+1; k < length; k = 2*k+1) {
            if(k+1 < length && less(arr, k, k+1)) {
                k++;
            }

            //如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
            if(arr[k] > tmp) {
                arr[i] = arr[k];
                i = k;
            } else {
                break;
            }
        }

        arr[i] = tmp; // 当tmp值放到最终的位置
    }

    private static void less(int[] arr, int i, int j) {
        if(arr[i] < arr[j]) {
            return true;
        } else {
            return false;
        }
    }

}

五、快速排序

基本思想：挖坑填数+分治法

①. 从数列中挑出一个元素，称为”基准”（pivot）。
②. 重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
③. 递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。

public static void quickSort(int[] arr, int low, int high) {
    if(arr == null || arr.length <= 0) {
        return;
    }

    int left = low;
    int right = high;
    int tmp = arr[left];

    while(left < right) {
        while(left < right && arr[right] >= tmp) {
            right--;
        }

        arr[left] = arr[right];

        while(left < right && arr[left] <= tmp) {
            left++;
        }
        
        arr[right] = arr[left];
    }

    arr[left] = tmp;
    quickSort(arr, low, left-1);
    quickSort(arr, left+1, high);
}

六、归并排序

基本思想：归并排序算法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

public class Solution {
    public static void mergeSort(int[] nums) {
        int[] tmp = new int[nums.length];

        mergeSort(nums, tmp, 0, nums.length-1);
    }

    private static void mergeSort(int[] nums, int[] tmp, int left, int right) {
        if(left < right) {
            int mid = (left + right) >> 1;
            mergeSort(nums, tmp, left, mid);
            mergeSort(nums, tmp, mid+1, right);
            merge(nums, tmp, left, mid+1, right);
        }
    }

    private static void merge(int[] nums, int[] tmp, int leftPos, int rightPos, int rightEnd) {
        int leftEnd = rightPos-1;
        int tmpPos = leftPos;
        int numElements = rightEnd-leftPos+1;

        while(leftPos <= leftEnd && rightPos <= rightEnd) {
            if(nums[leftPos] <= nums[rightPos]) {
                tmp[tmpPos++] = nums[leftPos++];
            } else {
                tmp[tmpPos++] = nums[rightPos++];
            }
        }

        while(leftPos <= leftEnd) {
            tmp[tmpPos++] = nums[leftPos++];
        }

        while(rightPos <= rightEnd) {
            tmp[tmpPos++] = nums[rightPos++];
        }

        for(int i = 0; i < numElements; i++, rightEnd--) {
            nums[rightEnd] = tmp[rightEnd];
        }
    }
}

七、基数排序

它是这样实现的：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后，数列就变成一个有序序列。

基数排序按照优先从高位或低位来排序有两种实现方案：

• MSD（Most significant digital） 从最左侧高位开始进行排序。先按k1排序分组, 同一组中记录, 关键码k1相等, 再对各组按k2排序分成子组, 之后, 对后面的关键码继续这样的排序分组, 直到按最次位关键码kd对各子组排序后. 再将各组连接起来, 便得到一个有序序列。MSD方式适用于位数多的序列。

• LSD （Least significant digital）从最右侧低位开始进行排序。先从kd开始排序，再对kd-1进行排序，依次重复，直到对k1排序后便得到一个有序序列。LSD方式适用于位数少的序列。

public static void radixSort(int[] arr){
    if(arr.length <= 1) return;

    //取得数组中的最大数，并取得位数
    int max = 0;
    for(int i = 0; i < arr.length; i++){
        if(max < arr[i]){
            max = arr[i];
        }
    }

    // 最大数的位数
    int maxDigit = 1;
    while(max / 10 > 0){
        maxDigit++;
        max = max / 10;
    }

    //申请一个桶空间
    int[][] buckets = new int[10][arr.length];

    int base = 10;

    //从低位到高位，对每一位遍历，将所有元素分配到桶中
    for(int i = 0; i < maxDigit; i++){

        int[] bktLen = new int[10];//存储各个桶中存储元素的数量
        
        //分配：将所有元素分配到桶中
        for(int j = 0; j < arr.length; j++){
            int whichBucket = (arr[j] % base) / (base / 10);
            buckets[whichBucket][bktLen[whichBucket]] = arr[j];
            bktLen[whichBucket]++;
        }

        //收集：将不同桶里数据挨个捞出来,为下一轮高位排序做准备,由于靠近桶底的元素排名靠前,因此从桶底先捞
        int k = 0;
        for(int b = 0; b < buckets.length; b++){

            for(int p = 0; p < bktLen[b]; p++){
                // important here
                arr[k++] = buckets[b][p];
            }
        }

        base *= 10;
    }
}

参考：

https://www.cnblogs.com/skywang12345/p/3597597.html

https://blog.csdn.net/hguisu/article/details/7776068

https://www.cnblogs.com/chengxiao/p/6129630.html