正方形大阵
【问题描述】
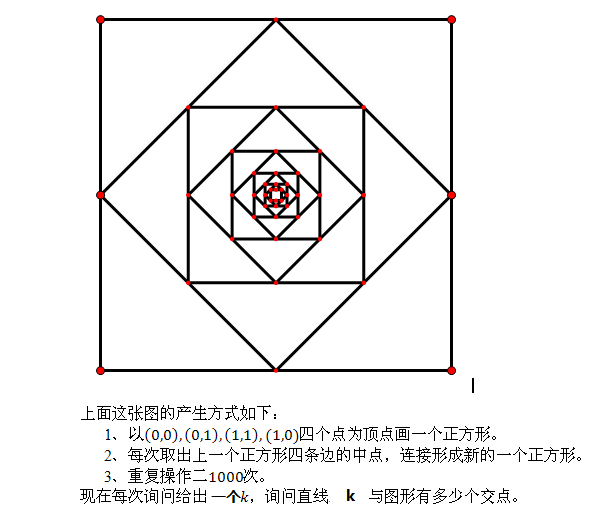
【输入格式】
第一行一个正整数n代表询问次数。
接下来n行每行一个不超过八位的小数k代表一组询问。
【输出格式】
输出共n行,代表每次询问的答案;如果有无数个交点,输出“-1”。
【输入样例】
3 0.375 0.001 0.478
【输出样例】
-1 4 20
【数据规模与约定】
100%的数据满足1<=n<2*1000,0<k<0.5。
【试题分析】
其实这实际上就是一道数学题,我们其实就知道第一个三角形的高、第二个高、第三个高……
由题可判断出:第二个三角形的高*2=第一个三角形的高。
其实我们可以根据勾股定理:0.5^2+0.5^2=0.5(第二个正方形的面积)
那么我们需要用第二个正方形的面积-第三个正方形的面积=4*第一个三角形的面积
第三个正方形的面积:根号(0.5/2)^2*2=1/4
第二个正方形减去第三个正方形:0.5-0.25=0.25
除4:0.25/4=0.0625
三角形面积为0.0625
由此可推出三角形高为0.25
第二个三角形的高:0.125
以此类推……
我们只需要判断输入的数在那个区间内。
我们可以继续数点:第一个区间(0~0.25)交点个数为4,第二个为8……
所以这道题就非常简单喽……
【代码】
#include<iostream>
using namespace std;
double a[2004],A[2004];
int b[2004];
int n;
double k;
void init()
{
a[1]=0.25;
A[1]=0.25;
a[0]=0;
b[0]=4;
for(int i=2;i<=2001;i++) {A[i]=(double)A[i-1]/2;}
for(int i=2;i<=2001;i++) {a[i]=(double)(a[i-1]+(double)A[i]);}
for(int i=1;i<=2001;i++) b[i]=b[i-1]+4;
}
void ans(double k)
{
for(int i=1;i<=2001;i++) if(a[i]==k) {cout<<"-1"<<endl;return ;}
for(int i=1;i<=2001;i++) if(a[i-1]<k&&a[i]>k) {cout<<b[i-1]<<endl;return ;}
}
int main()
{
init();
cin>>n;
while(n--)
{
cin>>k;
ans(k);
}
}