3743. Alice and Bob

题目描述

Sample Input
输入1：

4

1 2 2 3

输入2：

4

1 1 2 3

Sample Output
输出1：

5

输出2：

5

N<=10^5

题解

注意给出的是a

一种神奇的做法

从后往前求max(b[i])，假设b[i+1]~b[n]已经求出，考虑能转移到b[i]的b[j]

设pre[i]表示最后一个a[i]-1的位置（a[0]=0），把(i,a[i])丢到笛卡尔坐标系上，从(i,a[i])向(pre[i],a[pre[i]])连线，则图形成一棵树

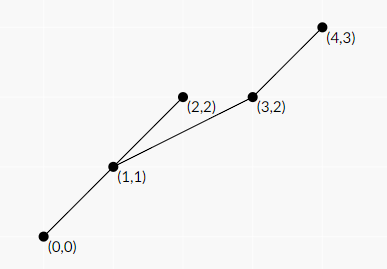
若b[j]能转移到b[i]，那么i向下做一条不经i点的射线，把射线经过的边断开，则必然能把j点与0点分开

如图，则b[2]可以由b[3]和b[4]转移，但b[3]不能由b[4]转移

证明：

线的实质就是x=a时a数组的转移情况，现要使b最大，那么就要把x尽量上移

如果x[i]经过了一条线，则会导致a[i]改变，不满足要求

---

每次可以把一个点以及其后面的点的答案向pre传，同时维护以a为关键字的线段树即可

code

#include <bits/stdc++.h>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define max(a,b) (a>b?a:b)
#define min(a,b) (a<b?a:b)
#define fout
using namespace std;

int tr[500002];
int a[100002];
int f[100002];
int f2[100002];
int ls[100002];
int pre[100002];
int n,i,j,k,l;
long long ans;

void change(int t,int l,int r,int x,int s)
{
	int mid=(l+r)/2;
	
	tr[t]=max(tr[t],s);
	if (l==r) return;
	
	if (x<=mid)
	change(t*2,l,mid,x,s);
	else
	change(t*2+1,mid+1,r,x,s);
}

int find(int t,int l,int r,int x,int y)
{
	int mid=(l+r)/2,s,ans=0;
	
	if (x<=l && r<=y)
	return tr[t];
	
	if (x<=mid)
	s=find(t*2,l,mid,x,y),ans=max(ans,s);
	if (mid<y)
	s=find(t*2+1,mid+1,r,x,y),ans=max(ans,s);
	
	return ans;
}

int main()
{
	freopen("alice.in","r",stdin);
	#ifdef fout
	freopen("alice.out","w",stdout);
	#endif
	
	scanf("%d",&n);
	fo(i,1,n)
	scanf("%d",&a[i]);
	
	fo(i,1,n)
	{
		pre[i]=ls[a[i]-1];
		ls[a[i]]=i;
	}
	
	fd(i,n,1)
	{
		f[i]=find(1,0,n,0,a[i]-1)+1;
		
		f2[i]=max(f2[i],f[i]);
		f2[pre[i]]=max(f2[pre[i]],f2[i]);
		
		change(1,0,n,a[i],f2[i]);
		change(1,0,n,a[pre[i]],f2[pre[i]]);
	}
	
	fo(i,1,n)
	ans+=f[i];
	
	printf("%lld
",ans);
	
	fclose(stdin);
	fclose(stdout);
	
	return 0;
}