疑惑核

2020.10.31

题目描述

求异或和 (1leq a，bleq 2^{63}-1)，答案对 (23333333333333333) （质数）取模

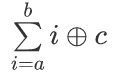
解法

先转换为前缀做差，设 (f(x)) 表示 ([0,x]) 的数的异或和。答案就是 (f(b)-f(a-1))

因为是异或，不同位间不会产生影响，所以考虑把每一位分开算贡献。若 (c) 的第 (i) 位是 (v_i)，那么贡献就是 (a) 到 (b) 的所有数中第 (i) 位是 (v_i xor 1) 的数的出现次数乘上 (1<<i) 。

求 (f(x))。记 (ned=v_i xor 1)，(lim) 表示 (x) 的第 (i) 位是多少，则 (lim=(x>>i)&1)。可以分三种情况快速求出每一位需要的值的个数：

1. (ned=lim)。那么此时第 (i) 位取到上限，若第 (i) 位之前的都取到上界（1种），则后面的数都不能超过上界，贡献为后面的数个个数加一（有0），即 (x-((x>>i)<<i)+1)，总的贡献为 ((x-((x>>i)<<i)+1) imes(1<<i))
2. (ned=1，lim=0)。若前面取到上界，那么当前为就取不到 (1)，那么前面一定不能取上界，因此后面的数就可以随便取。前面的贡献是 ((x>>(i+1)))，后面的贡献是 (1<<i) ，根据乘法原理总的贡献是 ((x>>(i+1)) imes(1<<i) imes(1<<i))
3. (ned=0,lim=1)。前面的只要不超过上界就行了，贡献为 ((x>>(i+1))+1) （有0），因为第 (i) 位要取 (0)，就没有达到上界，后面的可以随便取。总的贡献为 (((x>>(i+1))+1） imes(1<<i) imes(1<<i))。

时间复杂度 (Theta(log n))

Tips

这是一个恶心的模数，边模边乘都会爆，从 (100) 炸到 (10)，需要加上龟速乘。

#include<stdio.h>
#include<string.h>
#define LL long long
#define Mod 23333333333333333LL

int T;
LL a,b,c;

LL Mul(LL x,LL y){
    LL ret=0,len=0;
    while(y>=(1LL<<len)){
        if(y&(1LL<<(len++))) ret=(ret+x)%Mod;
        x=(x+x)%Mod;
    }
    return ret;
}

LL calc(LL x){
    LL ans=0;
    for(int i=0;i<63;i++){
        int lim=(x>>i)&1LL,ned=((c>>i)&1LL)^1LL;
        if(lim==ned){
            LL ret=(x-((x>>i)<<i)+1LL)%Mod;
            ret=(ret+Mul((x>>(i+1))%Mod,(1LL<<i)%Mod))%Mod;
            ans=(ans+Mul(ret,(1LL<<i)%Mod))%Mod;
        }else if(lim){
            LL ret=Mul(((x>>(i+1))+1)%Mod,(1LL<<i)%Mod);
            ans=(ans+Mul(ret,(1LL<<i)%Mod))%Mod;
        }else{
            LL ret=Mul((x>>(i+1))%Mod,(1LL<<i)%Mod);
            ans=(ans+Mul(ret,(1LL<<i)%Mod))%Mod;
        }
    }
    return ans;
}

int main(){
    freopen("sum.in","r",stdin);
    freopen("sum.out","w",stdout);
    scanf("%d",&T);
    while(T--){
        scanf("%lld%lld%lld",&a,&b,&c);
        printf("%lld
",((calc(b)-calc(a-1))+Mod)%Mod);
    }
}
/*
1
30217346 1530633997 1331237392
*/