【简介】
解决LCA问题的Tarjan算法利用并查集在一次DFS(深度优先遍历)中完成所有询问。换句话说,要所有询问都读入后才开始计算,所以是一种离线的算法。
【原理】
先来看这样一个性质:当两个节点(u,v)的最近公共祖先是x时,那么我们可以确定的说,当进行后序遍历的时候,必然先访问完x的所有子树,其中包含u、v,然后才会返回到x所在的节点。这个性质就是我们使用Tarjan算法解决最近公共祖先问题的核心思想。
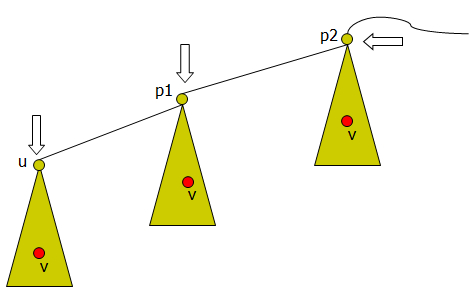
如上图所示,找出根节点到u得关键路径P ,已遍历的点位于路径P中某个点的子树中,当遍历到u时v已遍历过(u的子树已遍历完),那么v必然存在于子树pk中,此时LCA(u,v)就等于现在v所在集合的祖先pk。如果还没有遍历到,则继续遍历,只不过LCA(u,v)要等到遍历到v时才能知道了,原理如上。需要注意的一点是,为了保持上图的性质,如果一个节点的一个子树遍历完了,需要合并该节点的子树集合。
tarjan算法的步骤是(当dfs到节点u时):
(一) 在并查集中建立仅有u的集合,设置该集合的祖先为u
(二) 对u的每个孩子v:
1. tarjan之
2. 合并v到父节点u的集合,确保集合的祖先是u
(三)设置u为已遍历
(四)处理关于u的查询,若查询(u,v)中的v已遍历过,则LCA(u,v)= v所在的集合的祖先
【举例】
 |
假设遍历完10的孩子,要处理关于10的请求了 可以发现集合的祖先便是LCA ! |
【HDU 2586】
换成Tarjan 离线算法来做。

1 #pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include <stdio.h> 3 #include <string.h> 4 #include <vector> 5 #include <cmath> 6 using namespace std; 7 int n,m; 8 struct edge 9 { 10 int d,v,next; 11 edge(){} 12 edge(int _d,int _v,int _next) 13 { 14 d=_d;v=_v;next=_next; 15 } 16 }data[80003]; 17 int map[40003]; 18 int pool; 19 void addedge(int s,int e,int v) 20 { 21 int t=map[s]; 22 data[pool++]=edge(e,v,t); 23 map[s]=pool-1; 24 } 25 int mset[40003]; 26 int find(int k) 27 { 28 if (mset[k]==-1) return k; 29 return mset[k]=find(mset[k]); 30 } 31 void uion(int a,int b) 32 { 33 int aa=find(a); 34 int bb=find(b); 35 mset[aa]=bb; 36 } 37 struct _que 38 { 39 int a,b; 40 _que(int q=0,int w=0){a=q;b=w;} 41 }; 42 vector<vector<_que> > ques; 43 vector<int > ans; 44 int ifv[40003]; 45 int dis[40003]; 46 int anc[40003]; 47 void tar(int cur) 48 { 49 ifv[cur]=1; 50 anc[cur]=cur; 51 int p=map[cur]; 52 while (p!=-1) 53 { 54 if (!ifv[data[p].d]) 55 { 56 dis[data[p].d]=dis[cur]+data[p].v; 57 tar(data[p].d); 58 uion(cur,data[p].d); 59 anc[find(cur)]=cur; 60 } 61 p=data[p].next; 62 } 63 ifv[cur]=2; 64 for (int i=0;i<(int)ques[cur].size();++i) 65 { 66 if (ifv[ques[cur][i].a]==2) 67 ans[ques[cur][i].b]=dis[cur]+dis[ques[cur][i].a]-2*dis[anc[find(ques[cur][i].a)]]; 68 } 69 } 70 int main() 71 { 72 int T; 73 scanf("%d",&T); 74 while (T--) 75 { 76 ques.clear(); 77 pool=0; 78 memset(map,-1,sizeof map); 79 memset(ifv,0,sizeof ifv); 80 memset(mset,-1,sizeof mset); 81 scanf("%d%d",&n,&m); 82 ques.resize(n); 83 int s,e,v; 84 for (int i=0;i<n-1;++i) 85 { 86 scanf("%d%d%d",&s,&e,&v); 87 addedge(s-1,e-1,v); 88 addedge(e-1,s-1,v); 89 } 90 dis[0]=0; 91 ans.resize(m); 92 for (int i=0;i<m;++i) 93 { 94 int u,v; 95 scanf("%d%d",&u,&v); 96 --u;--v; 97 ques[u].push_back(_que(v,i)); 98 ques[v].push_back(_que(u,i)); 99 } 100 tar(0); 101 for (int i=0;i<(int)ans.size();++i) 102 { 103 printf("%d ",ans[i]); 104 } 105 } 106 }
