2019 杭电多校 第一场

2019 Multi-University Training Contest 1

补题链接：2019 Multi-University Training Contest 1

1002 Operation (HDU-6579)

题意

给定包含 (n) 个数的序列，(m) 个询问。询问有两种操作，操作 (0) 表示在数组最后添加一个新元素，操作 (1) 表示查询区间 [l,r] 的子集的异或最大值。

询问强制在线。

题解

线性基 贪心

1004 Vacation (HDU-6581)

题意

一条路上有 (n + 1) 辆车。第 (i) 辆车的长度为 (l_i)，离终点的距离为 (s_i)，最大车速为 (v_i)，(i) 越大越靠近终点。每辆车不能超越前面的车，但车头可以贴在前面车的车尾。每辆车经过了终点，仍继续在路上跑。求第 (0) 辆车 (最后一辆车) 车头通过终点线的最少需多少时间。

题解

贪心 二分

二分时间。判断 (mid = (l + r) / 2) 时间能否最后一辆车到达，若能到达则 (r = mid)，否则 (l = mid)。

接下来是如何判断时间 (t) 内最后一辆车能否到达终点。

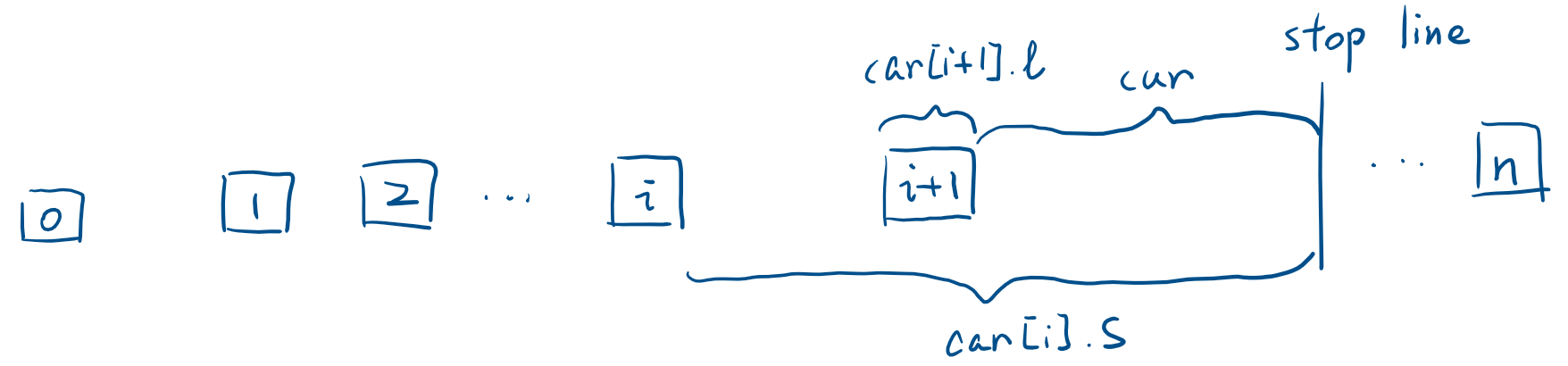
从第一辆车 (最靠近终点) 开始枚举，维护一个 (cur) 表示第 (i) 辆车车头到终点的距离。第 (i) 辆车经过 (t) 时间后可以行驶 (car[i].v * t) 的距离，距离终点 (car[i].s - car[i].v * t)。但是如果前面有车，就要比较前车车尾离终点的距离 (cur + car[i].l) 谁更近。如果 (car[i].s - car[i].v * t le cur + car[i].l)，也就是第 (i) 辆车行驶 (t) 时间后距离终点更近，那么由于不能超过前车，也就是只能贴在前车的车尾，(cur) 更新为前车车尾到终点的距离 (cur + car[i + 1].l)。如果 (car[i].s - car[i].v * t > cur + car[i].l)，也就是不会超过前车，那么 (cur) 就是当前车行驶 (t) 时间后车头距离终点的距离。如果第 (0) 辆车行驶 (t) 时间后 (cur le 0)，说明可以到达。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
const double eps = 1e-8;

struct CAR {
    int l, s, v;
} car[maxn];

int n;

int check(double x) {
    double cur = car[n].s - car[n].v * x;
    for (int i = n - 1; i >= 0; --i) {
        if (car[i].s - car[i].v * x <= cur + car[i + 1].l) cur += car[i + 1].l;
        else cur = car[i].s - car[i].v * x;
        if(cur > eps) return 0;
    }
    return cur <= eps;
}

int main() {
    while (~scanf("%d", &n)) {
        for(int i = 0; i < n + 1; ++i) {
            scanf("%d", &car[i].l);
        }
        for(int i = 0; i < n + 1; ++i) {
            scanf("%d", &car[i].s);
        }
        for(int i = 0; i < n + 1; ++i) {
            scanf("%d", &car[i].v);
        }
        double l = 0, r = 1e18;
        int cnt = 0;
        while (cnt < 100) {
            double mid = (l + r) / 2;
            if (check(mid)) r = mid;
            else l = mid;
            ++cnt;
        }
        printf("%.6lf
", r);
    }
    return 0;
}

1005 Path (HDU-6582)

题意

给定 (n) 个结点，(m) 条边的有向图，现在要删除一些边，使得结点 (1) 到 (n) 的最短路的长度增加，删除边的代价为边的权值，求最少的代价。

题解

最短路 最小割

首先要找出所有的最短路，得到最短路图。对最短路图求最小割就是答案。

所有最短路的求法：先跑一遍单源最短路，可以用 (Dijkstra) 算法。(Dijkstra) 算法得到的是起点到所有点的最短距离，存放在 (d) 数组中。那么遍历所有的边，如果 (d[i] + w_{ij} = d[j]) ((w_{ij}) 表示结点 (i) 到结点 (j) 的边的权值)，那么该条边一定在最短路图上。

至于最小割用 (Dinic) 算法求解即可。

1013 Code (HDU-6590)

题意

给出两类点的坐标，问能否用一条直线将两类点分开。

题解

题目看懂了就很好做了。

就是分别对两类点求凸包，然后判断两个凸包是否相交。若不相交，则能够用一条直线分开两类点，否则不能。

其实就是判断凸包是否相交的模板题。

#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
const double pi = acos(-1.0);
class Point {
public:
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
    Point operator+(Point a) {
        return Point(a.x + x, a.y + y);
    }
    Point operator-(Point a) {
        return Point(x - a.x, y - a.y);
    }
    bool operator<(const Point &a) const {
        if (x == a.x)
            return y < a.y;
        return x < a.x;
    }
    bool operator==(const Point &a) const {
        if (fabs(x - a.x) < eps && fabs(y - a.y) < eps)
            return 1;
        return 0;
    }
    double length() {
        return sqrt(x * x + y * y);
    }
};

typedef Point Vector;

double cross(Vector a, Vector b) {
    return a.x * b.y - a.y * b.x;
}

double dot(Vector a, Vector b) {
    return a.x * b.x + a.y * b.y;
}

bool isclock(Point p0, Point p1, Point p2) {
    Vector a = p1 - p0;
    Vector b = p2 - p0;
    if (cross(a, b) < -eps)
        return true;
    return false;
}

double getDistance(Point a, Point b) {
    return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}

typedef vector<Point> Polygon;
Polygon Andrew(Polygon s) {
    Polygon u, l;
    if(s.size() < 3) return s;
    sort(s.begin(), s.end());
    u.push_back(s[0]);
    u.push_back(s[1]);
    l.push_back(s[s.size() - 1]);
    l.push_back(s[s.size() - 2]);
    for(int i = 2 ; i < s.size() ; ++i) {
        for(int n = u.size() ; n >= 2 && !isclock(u[n - 2], u[n - 1], s[i]); --n) {
            u.pop_back();
        }
        u.push_back(s[i]);
    }
    for(int i = s.size() - 3 ; i >= 0 ; --i) {
        for(int n = l.size() ; n >=2 && !isclock(l[n-2],l[n-1],s[i]); --n) {
            l.pop_back();
        }
        l.push_back(s[i]);
    }
    for(int i = 1 ; i < u.size() - 1 ; i++) l.push_back(u[i]);
    return l;
}

int dcmp(double x)  {
    if (fabs(x) <= eps)
        return 0;
    return x > 0 ? 1 : -1;
}

// 判断点在线段上
bool OnSegment(Point p, Point a1, Point a2) {
    return dcmp(cross(a1 - p, a2 - p)) == 0 && dcmp(dot(a1 - p, a2 - p)) < 0;
}

// 判断线段相交
bool Intersection(Point a1, Point a2, Point b1, Point b2) {
    double c1 = cross(a2 - a1, b1 - a1), c2 = cross(a2 - a1, b2 - a1),
            c3 = cross(b2 - b1, a1 - b1), c4 = cross(b2 - b1, a2 - b1);
    return dcmp(c1) * dcmp(c2) < 0 && dcmp(c3) * dcmp(c4) < 0;
}

// 判断点在凸包内
int isPointInPolygon(Point p, vector<Point> s) {
    int wn = 0, cc = s.size();
    for (int i = 0; i < cc; i++) {
        Point p1 = s[i];
        Point p2 = s[(i + 1) % cc];
        if (p1 == p || p2 == p || OnSegment(p, p1, p2)) return -1;
        int k = dcmp(cross(p2 - p1, p - p1));
        int d1 = dcmp(p1.y - p.y);
        int d2 = dcmp(p2.y - p.y);
        if (k > 0 && d1 <= 0 && d2 > 0) wn++;
        if (k < 0 && d2 <= 0 && d1 > 0) wn--;
    }
    if (wn != 0) return 1;
    return 0;
}

void solve(Polygon s1, Polygon s2) {
    int c1 = s1.size(), c2 = s2.size();
    for(int i = 0; i < c1; ++i) {
        if(isPointInPolygon(s1[i], s2)) {
            printf("Infinite loop!
");
            return;
        }
    }
    for(int i = 0; i < c2; ++i) {
        if(isPointInPolygon(s2[i], s1)) {
            printf("Infinite loop!
");
            return;
        }
    }
    for (int i = 0; i < c1; i++) {
        for (int j = 0; j < c2; j++) {
            if (Intersection(s1[i], s1[(i + 1) % c1], s2[j], s2[(j + 1) % c2])) {
                printf("Infinite loop!
");
                return;
            }
        }
    }
    printf("Successful!
");
}

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        scanf("%d", &n);
        Polygon s1, s2;
        for (int i = 0; i < n; ++i) {
            double x1, x2, y;
            scanf("%lf%lf%lf", &x1, &x2, &y);
            if(y == 1) {
                s1.push_back(Point(x1, x2));
            } else {
                s2.push_back(Point(x1, x2));
            }
        }
        if(n == 1) {
            printf("Successful!
");
            continue;
        }
        if(s1.size()) s1 = Andrew(s1);
        if(s2.size()) s2 = Andrew(s2);
        solve(s1, s2);
    }
    return 0;
}