软工第一次个人作业

软工第一次个人作业

项目	内容
这个作业属于哪个课程	2020春季计算机学院软件工程(罗杰 任健)
这个作业的要求在哪里	个人项目作业
教学班级	006
项目地址	https://github.com/hxh-d2s/IntersectProject

一、PSP

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	10	10
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	60	100
· Design Spec	· 生成设计文档	0	0
· Design Review	· 设计复审 (和同事审核设计文档)	0	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	0	0
· Design	· 具体设计	60	120
· Coding	· 具体编码	180	240
· Code Review	· 代码复审	10	30
· Test	· 测试（自我测试，修改代码，提交修改）	60	80
Reporting	报告
· Test Report	· 测试报告	120	100
· Size Measurement	· 计算工作量	10	10
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	10
-	总计	540	700

二、解题思路描述

读完题目要求后，我决定先完成基础要求，如果顺利的话再继续完成附加题要求的部分
对于基础要求部分即求直线的交点个数，我先思考的是交点的求法和直线与交点的保存办法。一开始我考虑的是用点斜式来保存直线，即再直线（line）类中将k和b作为基础属性，但通过进一步思考发现这样的表示方法在计算垂直于x轴的直线（k无穷大）时不适用，最后查阅资料后决定使用一般式，即ax+by+c=0的表示方法，将a，b，c作为基础属性。
而算法方面我运用dp的思想，每加入一条直线都将其与之前加入的直线进行计算，算出交点后与两条相交直线各自的交点集进行比较，没有重复则加入该直线交点集。这样做虽然没有将复杂度降到O(n^2)以下，但比每次算出交点后要与全部交点集内的点进行比较要快。当然，如果斜率相同则直线平行，考虑题干中不会出现无限的交点所以直线不会重叠，因此跳过斜率相同的情况。
之后思考加入圆后的解题思路，加入圆后又出现了两种新情况，直线与圆相交和圆与圆相交。于是每加入一种图形，都需要将他和圆的集合还有直线的集合进行交点计算，最后将该图形加入所属的方法的图形集合。之后我又去搜索了计算交点，然后准备开始设计实现

三、设计实现过程

这次的在编程上花去了很多时间，主要原因有两个，一是数学不大好，二是经验不足。

• 实现直线交点计算

先说实现的事，我第一阶段就实现了直线之间的交点统计，将直线分为一个类，除了其基础属性（a，b，c）外还存储一个容器map用以存放这个直线的交点。除去垂直于x轴的直线，所有直线上的点每一个x都唯一确定一个y，所以map的key设为x（垂直于x轴的直线将y设为key）

class Line {
private:
    std::map<double, double> intersections;    //存储一条直线与其他图形所有的交点
    std::map<double, double>::iterator sec_iter;
public:
    double a;
    double b;
    double c;
    Line(double a, double b, double c);
    int addIntersection(double x, double y);
};

而计算直线与直线之间交点的方法是先排除斜率相同的情况，因为这种情况下直线必定平行。
对于相交的直线则用推导数学公式的方法解决

• 实现直线与圆交点计算

实现上又将圆单独分一个类（Circle类）这个类与Line类类似，有基础属性x，y，r来表示一个圆和一个map容器来存储圆上的交点，不同的是圆上的交点不能用x或者y坐标唯一标识，所以采用用角度标识交点的方法。
之后除了直线与直线的交点计算外，又多了圆与圆，直线与圆的交点计算，都通过数学方法推导公式求解。

class Circle {
private:
    std::map<double, double> intersections;    //存储个圆与其他图形所有的交点
    std::map<double, double>::iterator sec_iter;

public:
    double x;
    double y;
    double r;
    Circle(double x, double y, double r);
    int addIntersection(double x2, double y2);
};

• 实现上的困难和单元测试

首先就是数学不好导致公式推导错误。其次是由于这次是先写程序再写单元测试，所以第一次写出来是单文件，发现并不适用于单元测试，最后分文件重构了一下，导致这次作业对单元测试的适配程度不是很理想。
单元测试主要测试了一些边界条件，这次作业的边界条件比较多，有直线与直线相交、平行，直线与圆相交、相离、相切，圆与圆内含、外离、相交、相切

四、改进性能程序

运行测试程序包含1000个图形的计算
首先是使用set作为容器的情况

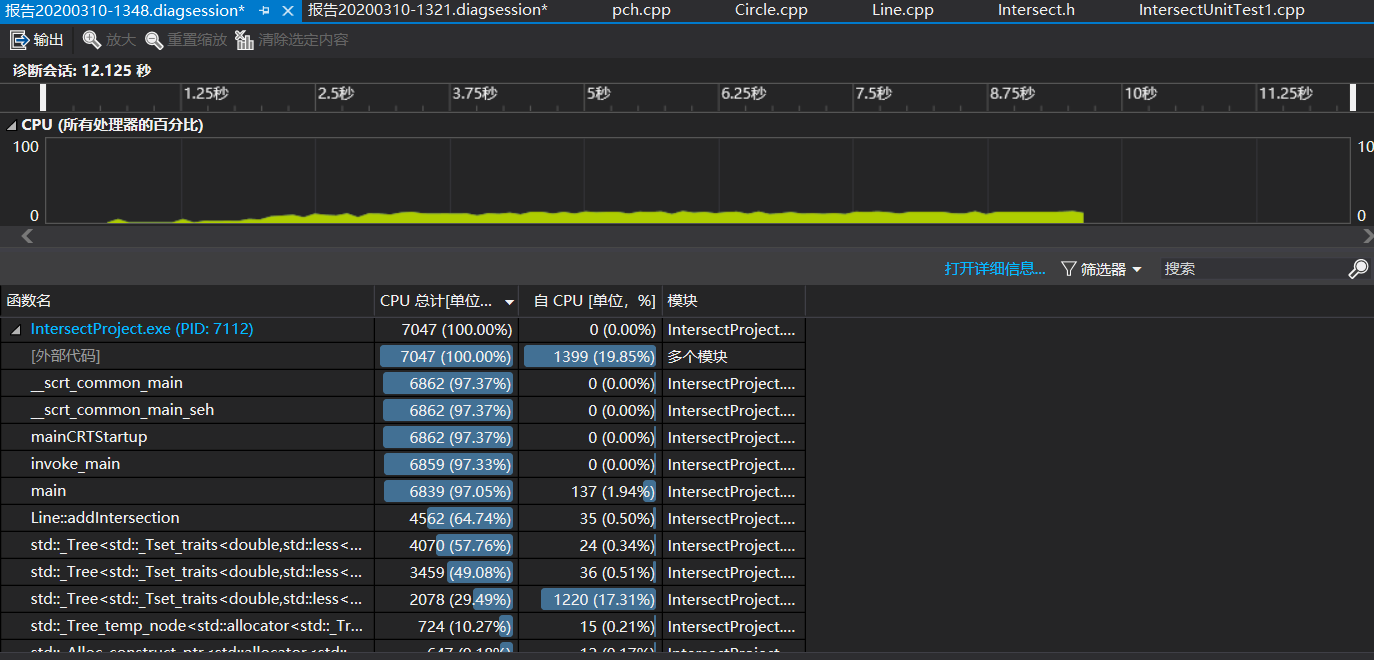
不难看出时间主要消耗在计算交点和往set里插入交点上。
这里考虑改进插入效率，由于每次插入时set都会重新排序消耗很多性能，故尝试将set容器替换为unordered_set容器。同时由于每个图形的交点容器只需要在比较时运用到key的部分，所以将unordered_set改为只存储一个数据而非数据对（pair）。

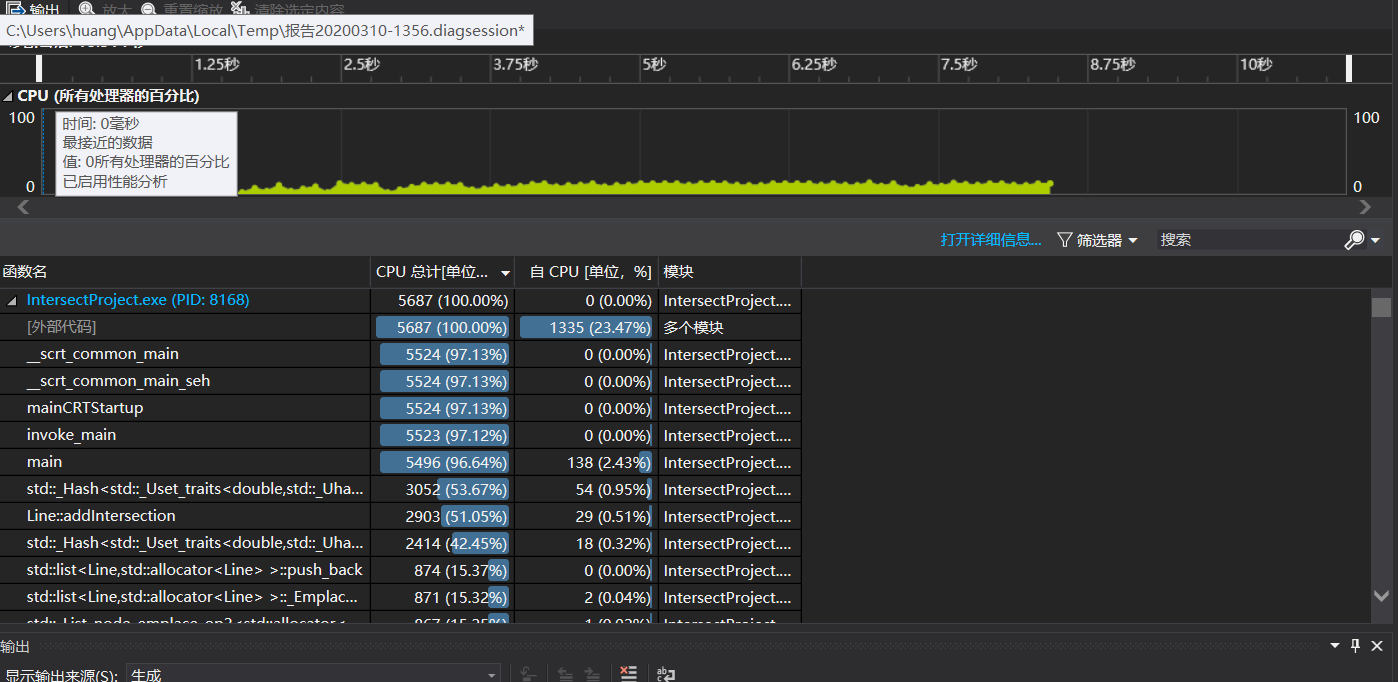
可以看出性能有了很大的提升，这里我又思考map的效果会怎么样，因此又进行了一次尝试

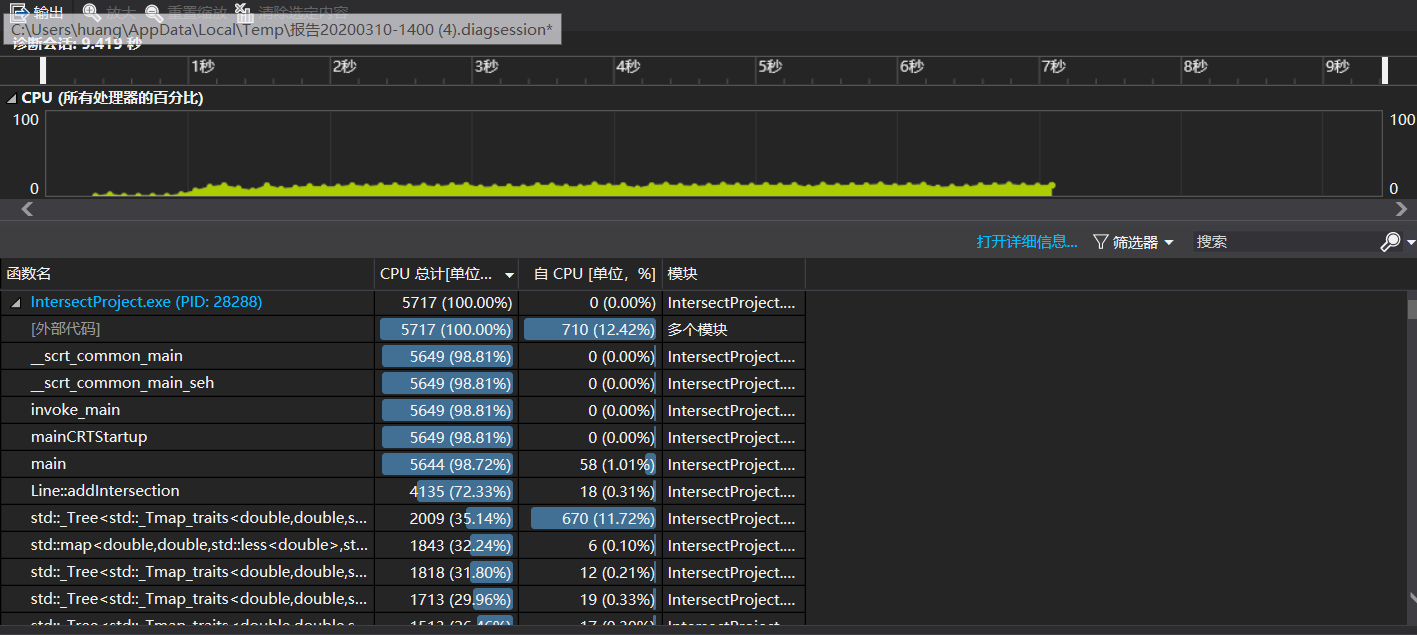
发现map的性能和unordered_set差不多，虽然addintersection的操作变多了但是外部调用变少了，考虑到可能是数据的影响因此试验了不同数据后发现是unordered_set性能更为优秀。因此最终采用了unordered_set的优化方案。

五、代码说明

这次作业中最麻烦的部分就是计算交点的部分，交点计算可以分为三种情况——直线与直线相交、直线与圆相交、圆与圆相交

• 直线与直线相交

if (a * b2 == a2 * b) {     //判断是否平行
    continue;
}
else {
    double m = a * b2 - a2 * b;
    double x = (c2 * b - c * b2) / m;
    double y = (c * a2 - c2 * a) / m;
    int sum = line_iter->addIntersection(x, y) + line.addIntersection(x, y);
    if (sum == 2) {
        count++;
        //cout << x << " " << y << endl;
    }
}

这部分的逻辑比较简单，就是联立解方程组求得交点的坐标。如果斜率相同则证明是平行，跳过计算

• 直线与圆相交

double d = fabs((a * x2 + b * y2 + c) / sqrt(a * a + b * b));
if (d > r)        //不相交
    continue;
else {            //相交或相切
    double m = -a * a - b * b;            //计算垂线与直线交点
    double x = ((a * y2 - b * x2) * b + c * a) / m;
    double y = (c * b - (a * y2 - b * x2) * a) / m;
    double t = sqrt((r * r - d * d) / (a * a + b * b));
    int sum = circle_iter->addIntersection(x+b*t, y-a*t) + line.addIntersection(x+b*t, y-a*t);
    if (sum == 2) {
        count++;
        //cout << x + b * t << " " << y - a * t  << endl;
    }
    sum = circle_iter->addIntersection(x-b*t, y+a*t) + line.addIntersection(x-b*t, y+a*t);
    if (sum == 2) {
        count++;
        //cout << x - b * t << " " << y + a * t << endl;
    }
}

这部分的逻辑是先计算出圆心到直线的距离d，根据d与r的关系判断直线与圆的位置关系，如果不相交则跳过计算。如果相交或相切则计算交点。交点的计算方法是先算出垂线与直线的交点，再根据d与r算出直线与圆交点交点相对垂足的位移计算得出两个交点坐标。如果相切则两个交点坐标相同。

• 圆与圆相交

double d = sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
if (d > r + r2 ||  d < fabs(r - r2))
    continue;
else {
    double t = acos((d * d + r * r - r2 * r2) / (2 * d * r));    //交点与圆心的夹角
    double m = atan2(y2 - y1, x2 - x1);                          //圆心与x轴的夹角
    double x = x1 + r * round(cos(m + t)*10000)/10000;
    double y = y1 + r * round(sin(m + t)*10000)/10000;
    int sum = circle_iter->addIntersection(x, y) + circle.addIntersection(x, y);
    if (sum == 2) {
       count++;
       //cout << x << " " << y << endl;
    }
    x = x1 + r * round(cos(m - t)*10000)/10000;
    y = y1 + r * round(sin(m - t)*10000)/10000;
    sum = circle_iter->addIntersection(x, y) + circle.addIntersection(x, y);
    if (sum == 2) {
       count++;
       //cout << x << " " << y << endl;
    }
}

先计算两个圆心之间的距离，判断两个圆的位置关系，外离或内含则跳过计算，否则算出两个交点。交点的算法为先通过余弦定理算出交点与圆心连线和圆心与圆心连线之间的夹角t，再计算出圆心与圆心连线和x轴之间的夹角m，则可根据角度和半径计算出两个交点的位置。

• 消除警告
  

六、总结

这次作业很好的教育了我要先架构再编程，我因为在直线改进到圆的过程中没有进行单元测试的规划导致后期必须对代码进行修改才能适用于单元测试，这也导致了我单元测试覆盖率不高，是次很好的教训
另一方面由于长久没使用C++导致了一定程度的生疏，在查资料上花费了很多时间，这也需要改进。