优化函数
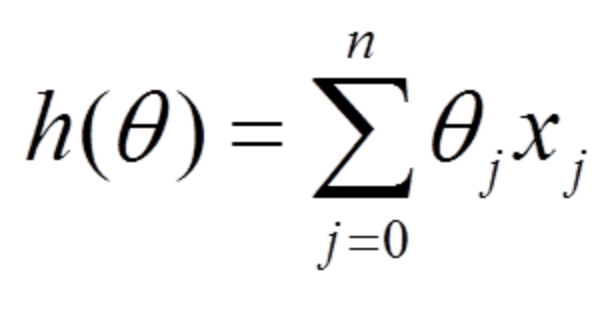
损失函数
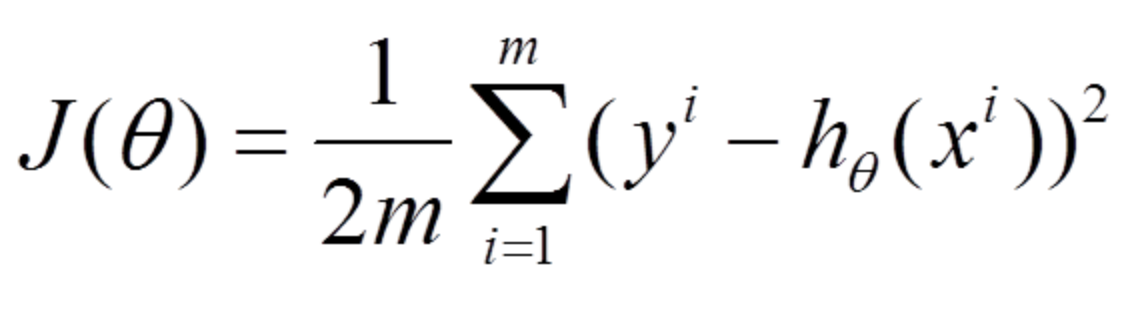
BGD
我们平时说的梯度现将也叫做最速梯度下降,也叫做批量梯度下降(Batch Gradient Descent)。
- 对目标(损失)函数求导
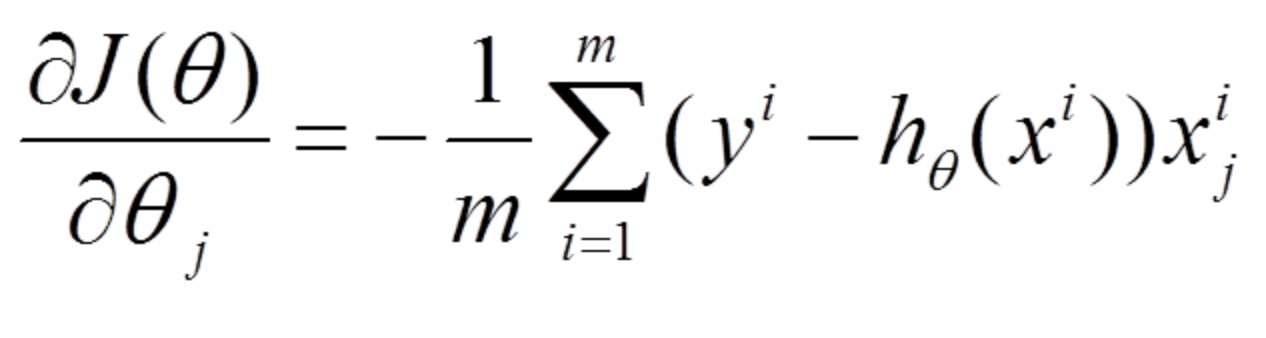
- 沿导数相反方向移动参数
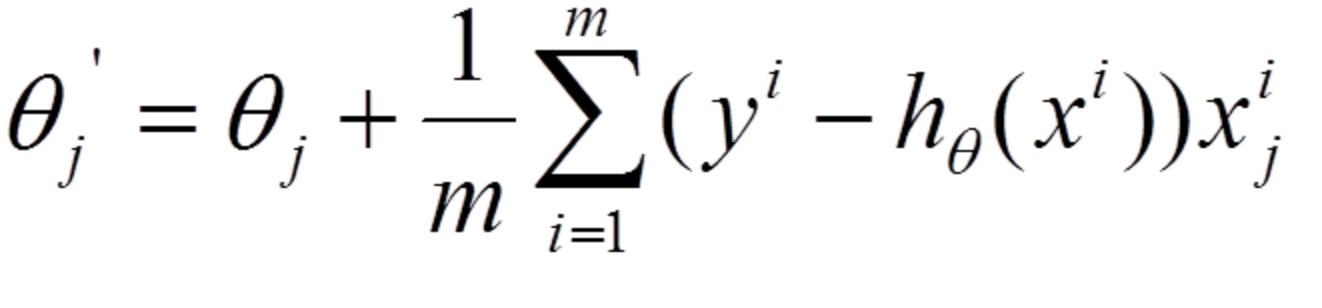
在梯度下降中,对于参数的更新,需要计算所有的样本然后求平均,其计算得到的是一个标准梯度(这是一次迭代,我们其实需要做n次迭代直至其收敛)。因而理论上来说一次更新的幅度是比较大的。
SGD
与BGD相比,随机也就是说我每次随机采用样本中的一个例子来近似我所有的样本,用这一个随机采用的例子来计算梯度并用这个梯度来更新参数,即SGD每次迭代仅对一个随机样本计算梯度,直至收敛。
-
由于SGD每次迭代只使用一个训练样本,因此这种方法也可用作online learning。
-
每次只使用一个样本迭代,若遇上噪声则容易陷入局部最优解。
mini-batch SGD
他用了一些小样本来近似全部的,其本质就是既然SGD中1个样本的近似不一定准,那就用更大的30个或50(batch_size)个样本来近似,即mini-batch SGD每次迭代仅对n个随机样本计算题都,直至收敛。
-
随机在训练集中选取一个mini-batch,每个mini-batch包含n个样本;(n<N,N为总训练集样本数)
-
在每个mini-batch里计算每个样本的梯度,然后在这个mini-batch里求和取平均作为最终的梯度来更新参数;(注意虽然这里好像用到了BGD,但整体整体mini-batch的选择是用到了SGD)
-
以上两步可以看做是一次迭代,这样经过不断迭代,直至收敛