FIR数字滤波器设计(窗函数法) C语言实现

背景介绍：

理想滤波器在物理上是不可实现的，其单位脉冲响应是无限长、非因果的。窗函数法，就是从时域出发，用有限长、因果的单位脉冲响应h(n)去逼近理想滤波器的无限长、非因果的单位脉冲响应的方法。窗函数法又叫傅里叶级数法。
更多背景资料，请看数字信号处理（李永全），P175。

方法简介：

设N-1阶FIR数字滤波器的单位冲击响应为h(n),则传递函数H(z)为：

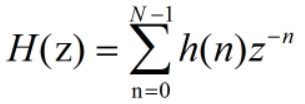
窗函数法的设计步骤如下：

1.根据给定的理想频率响应Hd(e^jw),利用傅里叶反变换，求出单位冲击响应hd(n):

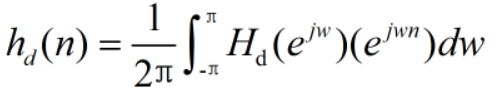
2.将hd(n)乘以窗函数w(n),得到所要求的FIR滤波器系数h(n):

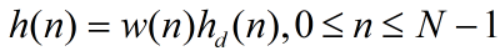
3.求卷积：

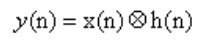
使用说明

1. 子函数语句：

void firwin(int n, int band, int wn, int fs, double h[], double kaiser=0.0, double fln=0.0, double fhn=0.0);

2. 形参说明

n：滤波器的阶数
band：滤波器的类型,取值1-4,分别为低通、带通、带阻、高通滤波器
wn：窗函数的类型，取值1-7，分别对应矩形窗、图基窗、三角窗、汉宁窗、海明窗、布拉克曼窗和凯塞窗
fs：采样频率
h：存放滤波器的系数
kaiser：beta值
fln：带通下边界频率
fhn：带通上边界频率

源代码

void firwin(int n, int band, int wn, int fs, double h[], double kaiser, double fln, double fhn)
{
    int i;
    int n2;
    int mid;
    double s;
    double pi;
    double wc1;
    double wc2;
    double beta;
    double delay;
    beta = kaiser;
    pi = 4.0 * atan(1.0);   //pi=PI;
    
    if ((n % 2) == 0)/*如果阶数n是偶数*/
    {
        n2 = (n / 2) - 1;/**/
        mid = 1;//
    }
    else
    {
        n2 = n / 2;//n是奇数,则窗口长度为偶数
        mid = 0;
    }
    
    delay = n / 2.0;
    wc1 = 2 * pi * fln;
    wc2 = 2 * pi * fhn;
    
    switch (band)
    {
    case 1:
    {
        for (i=0; i<=n2; ++i)
        {
            s = i - delay;
            h[i] = (sin(wc1 * s / fs) / (pi * s)) * window(wn, n+1, i, beta);//低通,窗口长度=阶数+1，故为n+1
            h[n - i] = h[i];
        }
        if (mid == 1)
        {
            h[n / 2] = wc1 / pi;//n为偶数时，修正中间值系数
        }
        break;
    }
    case 2:
    {
        for (i=0; i<=n2; i++)
        {
            s = i - delay;
            h[i] = (sin(wc2 * s / fs) - sin(wc1 * s / fs)) / (pi * s);//带通
            h[i] = h[i] * window(wn, n+1, i, beta);
            h[n-i] = h[i];
        }
        if (mid == 1)
        {
            h[n / 2] = (wc2 - wc1) / pi;
        }
        break;
    }
    case 3:
    {
        for (i=0; i<=n2; ++i)
        {
            s = i - delay;
            h[i] = (sin(wc1 * s / fs) + sin(pi * s) - sin(wc2 * s / fs)) / (pi * s);//带阻
            h[i] = h[i] * window(wn, n+1, i, beta);
            h[n - i] = h[i];
        }
        if (mid == 1)
        {
            h[n / 2] = (wc1 + pi - wc2) / pi;
        }
        break;
    }
    case 4:
    {
        for (i=0; i<=n2; i++)
        {
            s = i - delay;
            h[i] = (sin(pi * s) - sin(wc1 * s / fs)) / (pi * s);//高通
            h[i] = h[i] * window(wn, n+1, i, beta);
            h[n-i] = h[i];
        }
        if (mid == 1)
        {
            h[n / 2] = 1.0 - wc1 / pi;
        }
        break;
    }
    }
}

//n：窗口长度 type：选择窗函数的类型 beta：生成凯塞窗的系数
static double window(int type, int n, int i, double beta)
{
    int k;
    double pi;
    double w;
    pi = 4.0 * atan(1.0);  //pi=PI;
    w = 1.0;

    switch (type)
    {
    case 1:
    {
        w = 1.0;  //矩形窗
        break;
    }
    case 2:
    {
        k = (n - 2) / 10;
        if (i <= k)
        {
            w = 0.5 * (1.0 - cos(i * pi / (k + 1)));  //图基窗
        }
        if (i > n-k-2)
        {
            w = 0.5 * (1.0 - cos((n - i - 1) * pi / (k + 1)));
        }
        break;
    }
    case 3:
    {
        w = 1.0 - fabs(1.0 - 2 * i / (n - 1.0));//三角窗
        break;
    }
    case 4:
    {
        w = 0.5 * (1.0 - cos( 2 * i * pi / (n - 1)));//汉宁窗
        break;
    }
    case 5:
    {
        w = 0.54 - 0.46 * cos(2 * i * pi / (n - 1));//海明窗
        break;
    }
    case 6:
    {
        w = 0.42 - 0.5 * cos(2 * i * pi / (n - 1)) + 0.08 * cos(4 * i * pi / (n - 1));//布莱克曼窗
        break;
    }
    case 7:
    {
        w = kaiser(i, n, beta);//凯塞窗
        break;
    }
    }
    return(w);
}
static double kaiser(int i, int n, double beta)
{
    double a;
    double w;
    double a2;
    double b1;
    double b2;
    double beta1;

    b1 = bessel0(beta);
    a = 2.0 * i / (double)(n - 1) - 1.0;
    a2 = a * a;
    beta1 = beta * sqrt(1.0 - a2);
    b2 = bessel0(beta1);
    w = b2 / b1;
    return(w);
}
static double bessel0(double x)
{
    int i;
    double d;
    double y;
    double d2;
    double sum;
    y = x / 2.0;
    d = 1.0;
    sum = 1.0;
    for (i=1; i<=25; i++)
    {
        d = d * y / i;
        d2 = d * d;
        sum = sum + d2;
        if (d2 < sum*(1.0e-8))
        {
            break;
        }
    }
    return(sum);
}

得到系数之后，与输入信号求卷积即可！