对于判重,我们能想到的方法有什么??
①bool数组
②set(集)
数组与集合的优缺点:
1.因为集合是对数组做的封装,所以,数组永远比任何一个集合要快。
2.数组声明了它容纳的元素的类型,而集合不声明。这是由于集合以object形式来存储它们的元素。
3.一个数组实例具有固定的大小,不能伸缩。集合则可根据需要动态改变大小。
4.数组是一种可读/可写数据结构---没有办法创建一个只读数组。
③map(映射)
④hash
因为数组,set,map的适用范围是比较小的,而且速度很慢,所以今天我们就来研究一下hash!!!
哈希算法
* 回忆八数码问题:判重,给定一个九位数,怎么判断有没有在前面出现过?
* 考虑一种压缩数组的方法:如果我们想要把数组大小变为 N,那么对于一个数 X,存储在 X%N 的位置里面。
* 这样可以完美解决空间问题。

哈希算法 - 冲突
* 但存在一种情况:两个数 X 计算到了同一个位置(X%N = Y%N)
模数的确定: 取比元素个数大的质数
* 该如何解决?

* 第一种解决方式:顺序寻址法。
* 一直往后查询位置,直到有空为止。

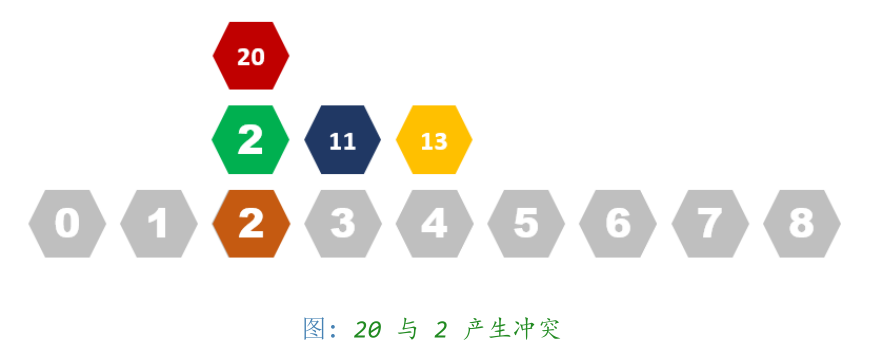

哈希算法 - 判断
* 如何判断这个数是否在之前已经出现过了?
* 类比插入过程,一直往后查询位置,直到出现两种情况之一。
-1 有空位:那就没出现过
-2 查询到一个相等的数:说明已经出现过了
哈希算法 - 顺序寻址法 - 代码实现
int hash_table[N]; // hash_table 哈希表:0 位置代表没有数 void push1(int x) { int y = x % N; // 计算初始位置,N:表的大小 for(; hash_table[y] && hash_table[y]!=x; ) y = (y+1) % N; // 寻找到一个 0 位置,或者找到自己为止 if(hash_table[y]) cout << x << "␣has␣occured␣before!" << endl; // 如果是自己本身,则之前已经出现过了 else { hash_table[y] = x; // 否则,将 x 加入表中 cout << x << "␣inserted." << endl; } }
哈希算法 - 冲突 - 解决的另一种方式
* 但存在一种情况:两个数 X 计算到了同一个位置(X%N = Y%N)
* 另一种解决方案:把所有数堆到一起(也就是用链表将模数相同的都连起来)

哈希算法 - 链地址法 - 代码实现
// 方法二:链地址法 vector<int> hash_array[N]; // hash_array:每个位置用一个 vector 来维护 void push2(int x) { int y = x % N; // 计算初始位置 for(int i=0; i<hash_array[y].size(); i++) if(hash_array[y][i] == x) // 如果之前已经出现过了 { cout << x << "␣has␣occured␣before!" << endl; return; // 标记已经出现过 } // 如果之前没有出现过,将 x 加入表中 hash_array[y].push_back(x); cout << x << "␣inserted." << endl; }
字符串哈希
* 十进制表示法——我需要计算出所有前缀所代表的数字。
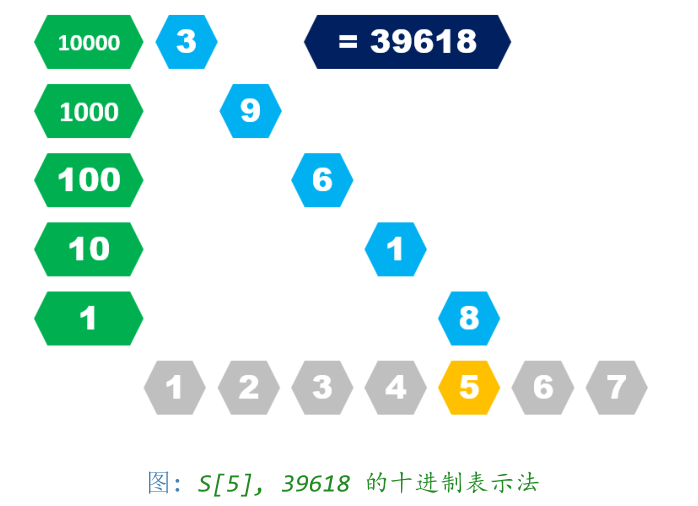
上图,在S[5]存的是39618,S[4]存的是3961,S[3]存的是396,S[2]存的是96,S[1]存的是6
* 假如需要计算区间 [l,r]所代表的数字 X,有
X = S[r] − S[l − 1] × 10r−l+1
字符串哈希 - 联系
* 数字和字符串有什么联系吗?我们可以把一个字符串看作是一个特殊的数字:
* 对于字符串“ABABC”,我们定义它的哈希值 H 为:H = ”A” ∗ D^4 + ”B” ∗ D^3 + ”A” ∗ D^2 + ”B” ∗ D + ”C”
- 其中 D 为一个规定的数。
D在字符串全为大写或者全为小写时,范围是26~27,当字符串中既有大写又有小写时,取52
* 那么我们可以把字符串看作是一个D 进制的数。计算方法和数字是类似的,而且对于相同字符串,得到的结果是相同的。
字符串算法 - 代码实现
string s; // s 为字符串 int f[N], g[N]; // f 为前缀和,g[i] 为 D 的 i 次方 void prehash(int n) // 预处理哈希值 { // 预处理时,注意到数字可能很大,对一个数 MD 取模 f[0] = 0; // f 前缀和预处理 for(int i=1; i<=n; i++) f[i] = (1LL * f[i-1] * D + s[i-1]) % MD; g[0] = 1; // g:D 次方预处理 for(int i=1; i<=n; i++) g[i] = 1LL * g[i-1] * D % MD; } int hash(int l, int r) // 计算区间 [l,r] 的哈希值 { int a = f[r]; int b = 1LL * f[l-1] * g[r-l+1] % MD; // 记得乘上次方 return (a - b + MD) % MD; // 前缀和相减 // 有可能结果小于 0,加上一个 MD 将其变为正数 } if(hash(a, b) == hash(c, d)) // 字符串 [a,b] 与字符串 [c,d] 匹配
字符串算法 - 几点注意事项
* 哈希算法:数组长度 N 用质数,减少冲突的次数,增加效率
* 字符串哈希:因为只是用一个小于 MD 的数来代表一个字符串,也是一种哈希;所以有可能会产生冲突(不同的字符串有相同的数),
- 可以通过前面的方法来解决:设哈希表(但速度很慢)。
- 解决方式:用质数来减少冲突的可能性;用几组不同的 D 与 MD。
// 哈希算法: N 使用质数 const int N = 1000003; // 字符串哈希: 多用质数,不容易产生冲突 const int D = 131; const int MD = 1e9 + 7; // 用几组不同的 D 与 MD const int D2 = 31; const int MD2 = 1e9 + 9;
自己选的路,跪着也要走完!!!