CF734E Anton and Tree

(mathtt{CF734E})

(mathcal{Description})

给一棵(n(nleq200000))个节点的树，每个点为黑色或白色，一次操作可以使一个相同颜色的连通块变成另一种颜色，求使整棵树变成一种颜色的最少操作数。

(mathcal{Solution})

这棵树中每个点为黑点或白点，然后最后也只要求出最小操作数，对于一个联通块，我们选择其中任何一个节点进行染色的效果是一样的（都会把这个联通块变成同一个颜色），于是我们自然而然的可以想到缩点。然后样例中的树就可以是

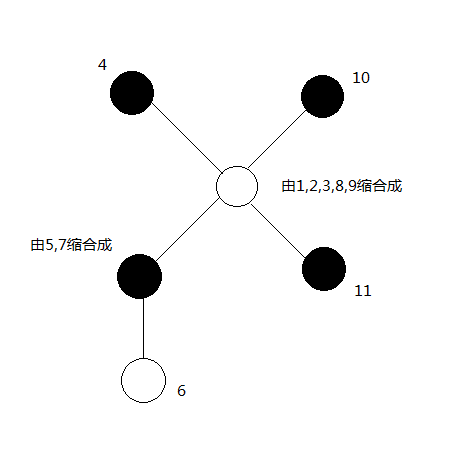
(贺个图(qwq))

可以看出我们把这个树从原先的树变成了一棵异层颜色相异（也就是黑白相间）的树，如果当前是一条链，我们要是最后操作数是最小的，我们一定会选择从中间开始染色，所以对于一棵树，我们只需要选择他的直径进行染色，最后的答案就是((直径+1)/ 2)。

(mathcal{Code})

#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;

int n, color[N];
vector<int> a[N];

inline int read() {
	int x = 0, k = 1; char c = getchar();
	for (; c < 48 || c > 57; c = getchar()) k ^= (c == '-');
	for (; c >= 48 && c <= 57; c = getchar()) x = x * 10 + (c ^ 48);
	return k ? x : -x;
}

pair<int, int> dfs(int x, int fa, int depth) {
    int sz = a[x].size();
    pair<int, int> tmp = make_pair(depth, x);
    for (int i = 0; i < sz; i++) {
        int y = a[x][i];
        if (y == fa)
            continue;
        if(color[y] != color[x])
            tmp = std::max(tmp, dfs(y, x, depth + 1));
        else 
            tmp = std::max(tmp, dfs(y, x, depth));
    }
    return tmp;
}

int main() {
    n = read();
    for (int i = 1; i <= n; i++)
        color[i] = read();
    for (int i = 1; i < n; i++) {
        int x = read(), y = read();
        a[x].push_back(y), a[y].push_back(x);
    }
    pair<int, int> tmp = dfs(1, -1, 0);
    tmp = dfs(tmp.second, -1, 0);
    printf("%d
", tmp.first + 1 >> 1);
}