1.图的遍历
1013 Battle Over Cities (25 分)
一种方法使用dfs求连通块的个数

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <vector> #define ll long long #define inf 0x3f3f3f3f #define pb push_back using namespace std; const int maxn = 1e4+100; int n, m, k, u, v, q; int d[maxn]; bool vis[maxn]; vector<int> g[maxn]; void dfs(int u){ vis[u] = 1; for(int i = 0; i < g[u].size(); i++){ int v = g[u][i]; if(v!=q&&!vis[v]) dfs(v); } } int main(){ scanf("%d%d%d", &n, &m, &k); while(m--){ scanf("%d%d", &u, &v); g[u].pb(v), g[v].pb(u); } while(k--){ scanf("%d", &q); for(int i = 1; i <= n; i++) vis[i] = 0; int cnt = 0; for(int i = 1; i <= n; i++){ if(i!=q&&!vis[i]) dfs(i), cnt++; } printf("%d ", cnt-1); } }
另外一种方法是用并查集,胡凡的做法对每次查询重新构建集合,这样感觉太慢了,没必要,本质都是求连通块的个数
1021 Deepest Root (25 分)
首先判断给定的图是否是颗树,需要知道的是连通、边数为n-1的图一定是棵树。输入的边数是n-1,我们只需要判断连通分量是否为1即可,可以通过并查集或者是dfs计数来判断。接下来只需要记录树的直径的端点,并按照顺序输出。注意不能加入重复的点,有个特殊样例n = 1可以用来测试

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <vector> #define ll long long #define inf 0x3f3f3f3f #define pb push_back using namespace std; const int maxn = 1e4+100; int n, u, v, tot, t, ans, f[maxn], cnt[maxn], s[maxn], node[maxn]; vector<int> g[maxn]; bool vis[maxn]; int find(int x){ if(f[x]!=x) f[x] = find(f[x]); return f[x]; } void merge(int x, int y){ x = find(x), y = find(y); f[x] = y; } void dfs(int u, int fa, int step){ if(ans<step) ans = step, s[1] = u, t = 1; else if(ans==step) s[++t] = u; for(int i = 0; i < g[u].size(); i++){ int v = g[u][i]; if(v!=fa) dfs(v, u, step+1); } } int main(){ scanf("%d", &n); for(int i = 1; i <= n; i++) f[i] = i; for(int i = 1; i <= n-1; i++){ scanf("%d%d", &u, &v); g[u].pb(v), g[v].pb(u); if(find(u)!=find(v)) merge(u, v); } for(int i = 1; i <= n; i++) cnt[find(i)]++; for(int i = 1; i <= n; i++) if(cnt[i]!=0) tot++; if(tot!=1) printf("Error: %d components", tot); else{ dfs(1, 0, 0); int k = 0; for(int i = 1; i <= t; i++) node[++k] = s[i], vis[s[i]] = 1; dfs(s[1], 0, 0); for(int i = 1; i <= t; i++) if(!vis[s[i]]) node[++k] = s[i], vis[s[i]] = 1; sort(node+1, node+1+k); for(int i = 1; i <= k; i++) printf("%d ", node[i]); } }
Reference:
树的直径及其证明:
https://www.cnblogs.com/Khada-Jhin/p/10195287.html
https://bbs.csdn.net/topics/340118243
1034 Head of a Gang (30 分)
题目要求满足条件的联通分量的信息,用并查集模拟即可,写的时候需要注意代码细节。特别提示:节点的total weight可以用和它相连的边权之和来表示。

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <vector> #define ll long long #define inf 0x3f3f3f3f #define pb push_back using namespace std; const int maxn = 1e5+100; int n, wei, val; int t, p[maxn], k, ans[maxn], dig[3]; int f[maxn], d[maxn], cnt[maxn], tot[maxn], u[maxn], v[maxn]; string s1, s2, str[maxn]; bool vis[maxn]; int find(int x){ if(f[x]!=x) f[x] = find(f[x]); return f[x]; } void merge(int x, int y){ x = find(x), y = find(y); d[x] < d[y] ? f[x] = y : f[y] = x; } int get_hash(string s){ int id = (s[0]-'A')*26*26+(s[1]-'A')*26+s[2]-'A'; str[id] = s; return id; } int main(){ scanf("%d%d", &n, &wei); for(int i = 1; i <= n; i++){ cin >> s1 >> s2 >> val; u[i] = get_hash(s1), v[i] = get_hash(s2); if(!vis[u[i]]) p[++t] = u[i], f[u[i]] = u[i], vis[u[i]] = 1; if(!vis[v[i]]) p[++t] = v[i], f[v[i]] = v[i], vis[v[i]] = 1; d[u[i]] += val, d[v[i]] += val; } for(int i = 1; i <= n; i++){ if(find(u[i])!=find(v[i])) merge(u[i], v[i]); } for(int i = 1; i <= t; i++) { int head = find(p[i]); cnt[head]++, tot[head] += d[p[i]]; } for(int i = 1; i <= t; i++){ int head = find(p[i]); if(cnt[head]<=2||tot[head]<=wei*2) continue; if(vis[head]) ans[++k] = head, vis[head] = 0; } sort(ans+1, ans+1+k); printf("%d ", k); for(int i = 1; i <= k; i++) printf("%s %d ", str[ans[i]].c_str(), cnt[ans[i]]); }
1076 Forwards on Weibo (30 分)
给出每个用户关注的人的id,和最多转发的层数,求一个id发了条微博最多会有多少个人转发
当时第一想法是DFS,最后还是AC了,不过过程相当曲折。
开始有几个点WA掉了,发现是因为用了vis标记访问过的id后就不再访问了,这显然是错误的,因为可能同一个节点可能会有不同的路径,对应的转发层数也不同。改掉之后,最后一个点TLE,于是开始剪枝,这里的方法是用vis记录节点转发的最小层数,只有源点到该节点的路径更短才会被遍历,这样保证每个节点转发的距离最远。另外在循环里面写递归出口比在外面写确实要更加省时些,关于DFS更详细的讨论参见Reference下的牛客链接

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <vector> #include <set> #define ll long long #define inf 0x3f3f3f3f #define pb push_back using namespace std; const int maxn = 1e4+100; int n, l, m, k, v, q, cnt; int t, head[maxn]; int vis[maxn]; vector<int> g[maxn]; void dfs(int u, int dep){ for(int i = 0; i < g[u].size(); i++){ int v = g[u][i]; if(dep+1>l||(vis[v]!=-1&&dep+1>=vis[v])) continue; if(vis[v]==-1) cnt++; vis[v] = dep+1; dfs(v, dep+1); } } int main(){ scanf("%d%d", &n, &l); for(int u = 1; u <= n; u++){ scanf("%d", &m); while(m--){ scanf("%d", &v); g[v].pb(u); } } scanf("%d", &k); while(k--){ scanf("%d", &q); for(int i = 1; i <= n; i++) vis[i] = -1; cnt = 0, vis[q] = 0, dfs(q, 0); printf("%d ", cnt); } }
写完后发现还是BFS更加适合,毕竟题目确实符合这种模型

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <vector> #include <set> #include <queue> #define ll long long #define inf 0x3f3f3f3f #define pb push_back #define pii pair<int,int> using namespace std; const int maxn = 1e4+100; int n, l, m, k, v, q, cnt; int t, head[maxn]; bool vis[maxn]; vector<int> g[maxn]; void bfs(){ queue<pii> que; que.push({q, 0}), vis[q] = 1; while(!que.empty()){ pii now = que.front(); que.pop(); int u = now.first, step = now.second; if(step==l) break; for(int i = 0; i < g[u].size(); i++){ int v = g[u][i]; if(vis[v]) continue; vis[v] = 1, cnt++; que.push({v, step+1}); } } } int main(){ scanf("%d%d", &n, &l); for(int u = 1; u <= n; u++){ scanf("%d", &m); while(m--){ scanf("%d", &v); g[v].pb(u); } } scanf("%d", &k); while(k--){ scanf("%d", &q); for(int i = 1; i <= n; i++) vis[i] = 0; cnt = 0, bfs(); printf("%d ", cnt); } }
Reference:
https://www.nowcoder.com/questionTerminal/920f0f6ad2b94d44b929e2d7f0afdc80
2.最短路径
1003 Emergency (25分)
大意是求最短路径的条数及路径的最大点权和,可能阅读理解能力有限,看完别人博客才知道题目要求的是路径的最大点权和
复习了下邻接表存图和Dijkstra找最短路,以下可以帮助理解Dijkstra算法:
大概是这样一个场景:往源点S注水,队列代表水目前能够流到的节点,队列里面标记了水流到节点的时刻。我们用优先队列模拟水流动的过程, 队头表示就是当前水流到的节点,这时与它相邻的节点也会被流到,更新节点被流到的时刻即可。显然点p第一次被水流到的时刻,就是S到p的最短路径(水的流速为1)。d[v]<p.first表示已经被水流过的节点不用进行处理了(已经处理过)

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <map> #include <queue> #include <vector> #include <cmath> #define ll long long #define pb push_back #define inf 0x3f3f3f #define pii pair<int, int> using namespace std; const int maxn = 1e4+100; struct edge{ int to, cost; }; vector<edge> g[maxn]; int n, m; int u, v, val, w[maxn]; int s, t, d[maxn], num[maxn], tot[maxn]; void dijkstra(){ for(int i = 1; i <= n; i++) d[i] = inf; priority_queue<pii, vector<pii>, greater<pii> >que; que.push({0, s}), d[s] = 0, num[s] = 1, tot[s] = w[s]; while(!que.empty()){ pii p = que.top(); que.pop(); int u = p.second; if(d[u]<p.first) continue; int cnt = g[u].size(); for(int i = 0; i < cnt; i++){ edge e = g[u][i]; int v = e.to, cost = e.cost; if(d[u]+cost<d[v]){ d[v] = d[u] + cost; tot[v] = tot[u] + w[v]; num[v] = num[u]; que.push({d[v], v}); } else if(d[u]+cost==d[v]){ tot[v] = max(tot[v], tot[u]+w[v]); num[v] += num[u]; } } } } int main(){ scanf("%d%d%d%d", &n, &m, &s, &t); for(int i = 0; i <= n-1; i++) scanf("%d%", &w[i]); while(m--){ scanf("%d%d%d", &u, &v, &val); g[u].pb({v, val}), g[v].pb({u, val}); } dijkstra(); //for(int i = 0; i <= n-1; i++) printf("%d ", d[i]); printf("%d %d", num[t], tot[t]); }
https://www.zhihu.com/question/68753603/answer/608934658
https://blog.csdn.net/CV_Jason/article/details/80891055
https://blog.csdn.net/u012161251/article/details/104151880
1018 Public Bike Management (30 分)
这题的意思看了半天发现还是有误差:
行驶路线是单向无往返的,也就是从管理中心出发,每到一个车站就要将该车站的单车数量调整为半满,不能利用返程调整。
例如:总容量为 10,S1为 2,S2为 8,路线 PBMC->S1->S2,不能从S2取 3 辆调度到 S1,需要从管理中心派送 3 辆,并带回 3 辆。
这样一来,就是求解S到T的最短路径。如果最短路径有多个,求能带的最少的自行车数目的那条。如果还是有很多条不同的路,那么就找一个从车站带回的自行车数目最少的(带回的时候是不调整的)。由于求解最短路的过程中,对于距离相同的路径的最优解并不是简简单单的判断,因此选择先求出所有的最短路,再从中挑选最优路径。
为了方便统计各车站的自行车是否需要派送/带走,输入数据是将节点的值处理成val[i] - c/2,方便之后的判断。
最后敲得时候出现了很多细节性问题,比如少了个%d、把u写成i、没有初始化minNeed和minRemain导致值未更新,写的时候需要多加考虑和细心

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <vector> #include <set> #include <queue> #define ll long long #define inf 0x3f3f3f3f #define pb push_back #define pii pair<int,int> using namespace std; const int maxn = 1e4+100; int c, n, t, m, val[maxn], d[maxn]; int minNeed = inf, minRemain = inf; vector<pii> g[maxn]; vector<int> pre[maxn], tmpPath, path; void dfs(int u){ if(u==0){ int remain = 0, need = 0; for(int i = tmpPath.size()-1; i >= 0; i--){ int v = tmpPath[i]; if(val[v]>0) remain += val[v]; else remain+val[v]<0 ? need += -val[v]-remain, remain = 0 : remain += val[v]; } if(need<minNeed){ minNeed = need, minRemain = remain; path = tmpPath; } else if(need==minNeed&&remain<minRemain){ minRemain = remain; path = tmpPath; } return; } tmpPath.pb(u); for(int i = 0; i < pre[u].size(); i++) dfs(pre[u][i]); tmpPath.pop_back(); } void dijkstra(){ for(int i = 1; i <= n; i++) d[i] = inf; priority_queue<pii, vector<pii>, greater<pii> >que; que.push({0, 0}); while(!que.empty()){ pii p = que.top(); que.pop(); int u = p.second; if(d[u]<p.first) continue; for(int i = 0; i < g[u].size(); i++){ int v = g[u][i].first, cost = g[u][i].second; if(d[u]+cost<d[v]){ d[v] = d[u] + cost; que.push({d[v], v}); pre[v].clear(), pre[v].pb(u); } else if(d[u]+cost==d[v]){ pre[v].pb(u); } } } } int main(){ scanf("%d%d%d%d", &c, &n, &t, &m); for(int i = 1; i <= n; i++) scanf("%d", &val[i]), val[i] -= c/2; while(m--){ int u, v, cost; scanf("%d%d%d", &u, &v, &cost); g[u].pb({v, cost}), g[v].pb({u, cost}); } dijkstra(); dfs(t); printf("%d 0", minNeed); for(int i = path.size()-1; i >= 0; i--) printf("->%d", path[i]); printf(" %d", minRemain); }
Reference:
https://lokka.me/2020/07/15/pat-a-1018/
https://blog.csdn.net/liuchuo/article/details/52316405
https://blog.csdn.net/zhang35/article/details/104153985
关于Dijkstra的理解,摒弃了之前照搬别人的想法:
在一棵树中,一个结点到另一个结点的路径是唯一的,但在图中,结点之间可能有多条路径,其中哪条路最近呢?这一类问题称为最短路径问题。最短路径问题也是 BFS 的典型应用,而且其方法与层序遍历关系密切。
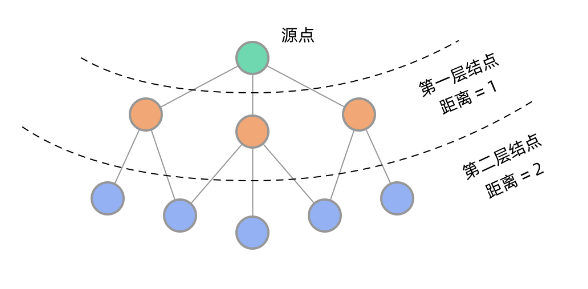
在二叉树中,BFS 可以实现一层一层的遍历。在图中同样如此。从源点出发,BFS 首先遍历到第一层结点,到源点的距离为 1,然后遍历到第二层结点,到源点的距离为 2…… 可以看到,用 BFS 的话,距离源点更近的点会先被遍历到,这样就能找到到某个点的最短路径了。
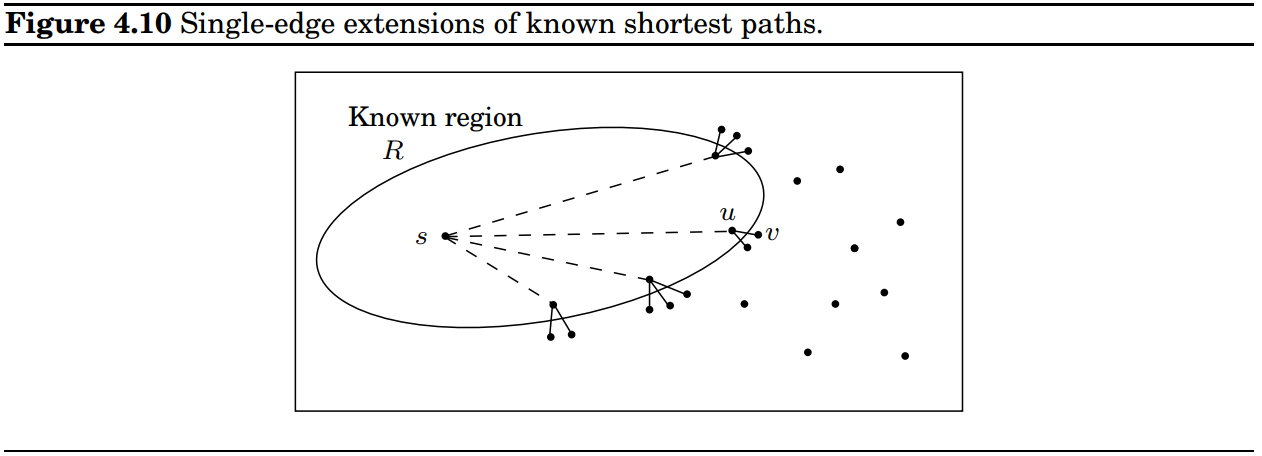
我们在原图的节点间中添加若干个节点使得它们的间距都为1,这时可以把Dijkstra看作成BFS。像蜻蜓点水一样,由近及远,层层往远处遍历,遍历到的点即是最短距离。但是很明显中间的若干节点不需要遍历到,模拟这个过程只需要保证水波边缘处于最近的层数即可。
参考自:
Algorithms - Sanjoy Dasgupta, Christos H. Papadimitriou, and Umesh V. Vazirani
https://segmentfault.com/a/1190000008235554
https://www.cnblogs.com/sbb-first-blog/p/13259728.html
严谨且生动的理解算法并不是一件容易的事情,特别是在认知和资源有限的情况下,但无疑这对学习帮助是巨大的,而且不仅仅只是对算法而言,细想其他课程也皆是如此。别人认为很好的理解方式放在自己这里并不一定能给自身同样的体会,这点是需要知道的,学完之后能用自己的语言表达出来才是真正清楚的。不过他人的思想和思考方式总会给你带来帮助
1072 Gas Station (30 分)
按照要求模拟求解即可,但是有个坑点就是:对于数据的数据应当使用字符串读入,不管是加油站G#还是房子#都应当用stoi转化成数字,因为你不知道后面会有几位数。测试样例4一开始是段错误,加油站的读入改成stoi转化后变为WA,这个bug害的我找了一下午,改了加油站的但没有改房子的数字转化,这就很要命了。

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <vector> #include <set> #include <queue> #define ll long long #define inf 0x3f3f3f3f #define pb push_back #define pii pair<int,int> using namespace std; const int maxn = 1e5+100; int n, m, k, ds; int mind = -1, id, d[maxn], sumd = inf; string s1, s2; struct node{ int to, cost; }; vector<node> g[maxn]; void dijkstra(int s){ priority_queue<pii, vector<pii>, greater<pii> >que; for(int i = 1; i <= n+m; i++) d[i] = inf; d[s] = 0, que.push({0, s}); while(!que.empty()){ pii p = que.top(); que.pop(); int u = p.second; if(d[u]<p.first) continue; for(int i = 0; i < g[u].size(); i++){ int v = g[u][i].to, cost = g[u][i].cost; if(d[v]>d[u]+cost){ d[v] = d[u] + cost; que.push({d[v], v}); } } } int mintmp = inf, sumtmp = 0; for(int i = 1; i <= n; i++){ if(d[i]>ds) return; mintmp = min(mintmp, d[i]); sumtmp += d[i]; } if(mintmp>mind) mind = mintmp, sumd = sumtmp, id = s; else if(mintmp==mind&&sumtmp<sumd) sumd = sumtmp, id = s; else if(mintmp==mind&&sumtmp==sumd) id = min(id, s); } int main(){ scanf("%d%d%d%d", &n, &m, &k, &ds); while(k--){ int u, v, w; cin >> s1 >> s2 >> w; s1[0]=='G'?u=stoi(s1.substr(1))+n:u=stoi(s1), s2[0]=='G'?v=stoi(s2.substr(1))+n:v=stoi(s2); g[u].pb({v, w}), g[v].pb({u, w}); } for(int i = n+1; i <= n+m; i++) dijkstra(i); if(mind==-1) printf("No Solution"); else printf("G%d %d.0 %.1lf", id-n, mind, 1.0*sumd/n); }
1087 All Roads Lead to Rome (30 分)
求满足条件的最短路径并回溯,和1018差别不大,甚至更加简单。不需要对路径用dfs进行筛选,满足最优子结构的求最短路的过程中就能搞定。唯一改正的bug就是最短路径的数目应当用数组迭代记录,而不是简单的使用一个变量,这点在脑海里面模拟一下便知。

#include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <iostream> #include <vector> #include <set> #include <map> #include <queue> #define ll long long #define inf 0x3f3f3f3f #define pb push_back #define pii pair<int,int> using namespace std; const int maxn = 2e6+100; int n, m, val, cost; int place[maxn], hp[maxn]; int d[maxn], sum[maxn], cnt[maxn], pre[maxn], num[maxn]; string scity, city, c1, c2; struct node{ int to, cost; }; vector<node> g[maxn]; map<int, string> mp, tmp; int citynum(string s){ return s[0]*26*26+s[1]*26+s[2]; } void dijkstra(){ for(int i = 2; i <= n; i++) d[place[i]] = inf; priority_queue<pii, vector<pii>, greater<pii> >que; que.push({0, place[1]}), num[place[1]] = 1; while(!que.empty()){ pii p = que.top(); que.pop(); int u = p.second; if(d[u]<p.first) continue; for(int i = 0; i < g[u].size(); i++){ int v = g[u][i].to, cost = g[u][i].cost; if(d[v]>d[u]+cost){ d[v] = d[u] + cost; que.push({d[v], v}); num[v] = num[u], pre[v] = u; sum[v] = sum[u] + hp[v], cnt[v] = cnt[u] + 1; } else if(d[v]==d[u]+cost){ num[v] += num[u]; if(sum[u]+hp[v]>sum[v]) pre[v] = u, sum[v] = sum[u] + hp[v], cnt[v] = cnt[u] + 1; else if(sum[u]+hp[v]==sum[v]&&cnt[u]+1<cnt[v]) pre[v] = u, cnt[v] = cnt[u] + 1; } } } } int main(){ cin >> n >> m >> scity; place[1] = citynum(scity), mp[place[1]] = scity; for(int i = 2; i <= n; i++) { cin >> city >> val; int now = citynum(city); place[i] = now, hp[now] = val, mp[now] = city; } while(m--){ cin >> c1 >> c2 >> cost; int u = citynum(c1), v = citynum(c2); g[u].pb({v, cost}), g[v].pb({u, cost}); } dijkstra(); int t = citynum("ROM"); printf("%d %d %d %d ", num[t], d[t], sum[t], sum[t]/cnt[t]); int now = t, k = 0; while(now!=0) tmp[++k] = mp[now], now = pre[now]; for(int i = k; i >= 2; i--) cout << tmp[i] << "->"; cout << "ROM"; }
Reference: