- 一、概念介绍
- 1.1、激光雷达传感器
- 1.2、Lidar数学模型
- 1.3、运动畸变
- 二、畸变去除
- 2.1、纯估计（ICP）
- 2.2、里程计辅助法(外部传感器辅助)
一、概念介绍
1.1、激光雷达传感器
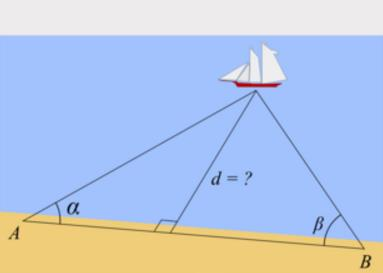
三角测距，例如：类似于双目测距原理，对于lidar，A是激光发射器，B是接收器
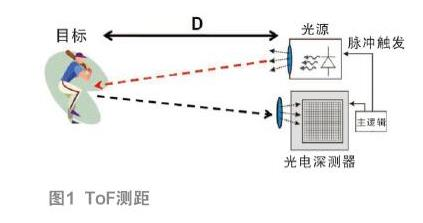
飞速时间差，没啥好说
三角测距 飞行时间(TOF)
- 中近距离精度较高(测距范围受基线距离限制) 测距范围广
- 价格便宜 （400-3000） 测距精度高
- 远距离精度较差 抗干扰能力强
- 易受干扰 价格昂贵(几万级别)
- 一般在室内使用 室内室外皆可
室内场景中，测距范围小于15m的时候，可以选用左边三角测距类型雷达；
如果是室外场景，选用TOF雷达（300线雷达 约等于 深度相机）
三角测距原理：
已知基线L(线段AB)、alpha、beta(这三个参数都是标定好的)，求解d，过于简单，不多BB
TOF测距原理：
略
1.2、激光雷达数学模型
前言：
我们知道目前的激光SLAM算法主要分为两种：基于滤波的SLAM和基于图优化的SLAM。而基于滤波的SLAM问题又是基于贝叶斯滤波的框架。因此我们不仅要问为什么需要使用贝叶斯来做滤波？
概念：什么是滤波？
滤波，即滤除噪声。我们知道在估计状态的过程中，控制引入运动噪声和观测引入传感器测量噪声。而滤波的实现是通过控制和观测获得的对同一状态不同的冗余信息（控制的预测信息和观测的测量信息）来减小位姿状态的不确定度，从而滤除控制和观测过程中的噪声。例如：若控制和观测的噪声都服从高斯分别，那么控制和观测得到的对状态估计也都是服从高斯分布。将两个高斯估计相乘得到后验分别的不确定度就会下降，从而达到滤波的效果。
原因：为什么用贝叶斯做滤波？
首先，从逻辑上讲，机器人SLAM的过程是：先控制机器人到达一个位姿，然后再进行观测。但是问题出现在了我们是由控制数据和观测数据来求机器人位姿，这就出现了一个逆向的过程即：我们是先有位姿再得到观测数据却变成了先得到观测数据再来求位姿的过程。通俗来讲就是我们需要由结果（观测数据）来反推原因（位姿）；因此这里就引入了贝叶斯公式，贝叶斯公式的存在就是为了求解这种由结果反推原因的问题；不懂的小伙伴可以看一下贝叶斯公式的由来。
这里参考：https://blog.csdn.net/liuyanpeng12333/article/details/81003340
1.2.1 光束模型(beam model)
激光的观测值的概率分布公式：
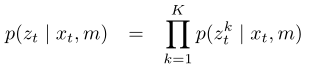
上式中，xt表示基线位置（好像不太对），m表示地图，zt表示观测到的距离值；p(zt | xt, m):已知地图，雷达基线位置，得到zt值的概率。（可参考书籍《概率机器人》）注：等式右边是连乘，我猜应该是为了求解极大似然，求解方法应该就是取负对数，转为求极小值。（概率可理解为：什么样的位姿xt，地图m才能导致现在的观测值是zt）
上述的距离观测概率值p(zt | xt, m)的分布有如下四种形式：
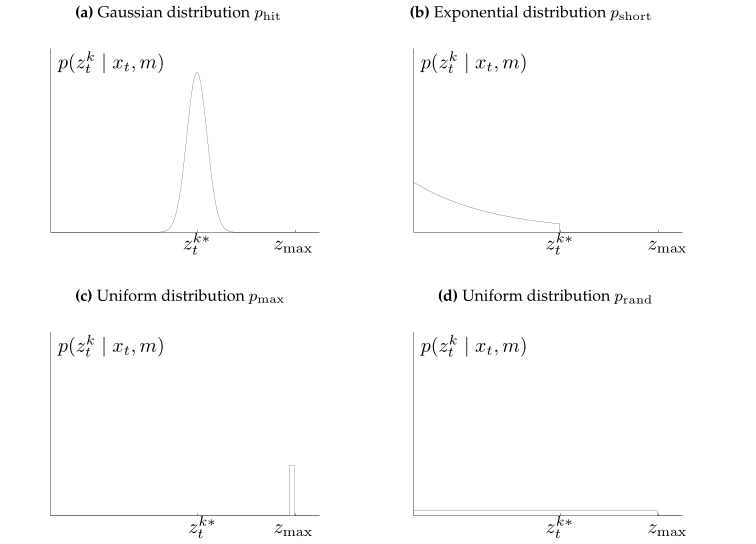
对上图的解释：
- a、常规测距的概率分布
- b、有遮挡物的时候的概率分布（讲课真尼玛水，几百的课程，也就这B样了）
- c、忽略不计
- d、忽略不计
p(zt | xt, m)也就是置信度得分（ score(zt) ），表示的是：当前这一束激光测距与地图重合程度，其实就是目标函数，作评价、优化用。
光束模型(beam model)缺点：
- 期望值的计算需要用raytracing,每一个位姿需要进行N次raytracing,N为一帧激光的激光束数量（计算量大，raytracing：光线追踪）。
- 在非结构化环境中(clutter),位姿微小的改变会造成期望值的巨大变化,从而导致得分进行突变。
- （假如机器人在t时刻，雷达的一帧点云中的某一束激光刚好观测到空间中的一个点，score = 1；在t+1时刻，机器人动了一点点，很可能没“看到”刚才那个点，这时候score = 0）
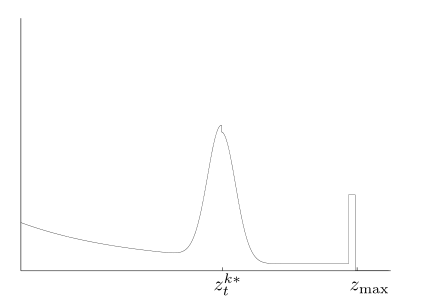
混合模型p(zt | xt, m)示意图
1.2.2 似然场模型(likelihood model)（劳资是没听懂讲的沙JB玩意）
- 对图像(如下右图，应该是深度图)进行高斯平滑,在任何环境中期望值对于位姿都是平滑的。
- 得分的计算不需要经过raytracking,直接通过查表即可得到,计算量低
- 同时适合结构化环境和非结构环境中
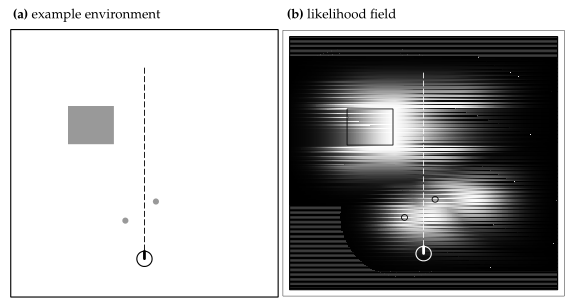
1.2、激光雷达运动畸变
雷达一般有运动畸变不变性的假设，如果你的雷达有50Hz，这种假设是很逼真的，但是如果只有5-10Hz，这种假设前提带来的误差就比较大，也就是运动畸变很大。
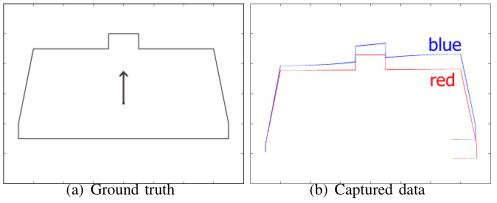
如上图(b)中，蓝色地图就是运动畸变导致的跑偏，原因有：
- 一帧数据激光点数据不是瞬时获得
- 激光测量时伴随着机器人的运动（所以严格意义上：只要机器人拖着雷达动，雷带采集一贞数据中的每一个点，都对应不同的机器人位姿；如果雷达帧率足够高，机器人运动幅度足够小，可以近似认为所有点对应同一个位姿，很多算法也是这样假设的）
- 激光帧率较低时,机器人的运动不能忽略
下一章节，说说怎么去除运动畸变
二、激光雷达运动畸变去除
2.1 基于纯估计法的畸变去除
这里用ICP算法去除畸变。
ICP算法懒得BB。
简单介绍下EM算法(马尔科夫）：
例如，我们要求解优化变量A、B，步骤：
- 1、固定A，优化B，直到损失函数最小化，
- 2、固定B，优化A，直到损失函数最小化，
- 不断重复过程1、2，直到收敛为止。
ICP算法可以看作EM算法的一个特例，在ICP算法中，R|t相当于A， 两帧点云中3D点对匹配关系相当于B；上图中，蓝色、红色两条线是一个ICP配准的过程。
ICP算法用在去除运动畸变的缺陷有：
- 没有考虑激光的运动畸变
- 当前激光数据的是错误的，则会导致算法误差很大(这好像是废话)
这里介绍ICP的变种算法VICP(velocity ICP)算法，没有忽略雷达的运动，但是假定雷达是匀速直线运动（比假定不动好一点）
上述机器人速度公式中，对于齐次矩阵T少写了一个ln(李群 -> 李代数)，T应该表示：当前帧 到 world 的变换，Vi是一个向量。 假定雷达采集一帧数据过程中，采样周期是Δt，所以有上述时刻表。
如何依据时刻 i 的位姿 Ti，得到时刻(ti - (n - j) Δt) 的位姿 T(ti - (n - j) Δt) ，如下公式，这两个时刻的时间差为 (n - j) *Δt，这里自然底数e表示：李代数 -> 李群。
所以可得运动矫正公式：
Note：速度Vi带了负号，因为当前时刻到历史时刻，方向是反的。
VICP算法流程和效果图如下图：
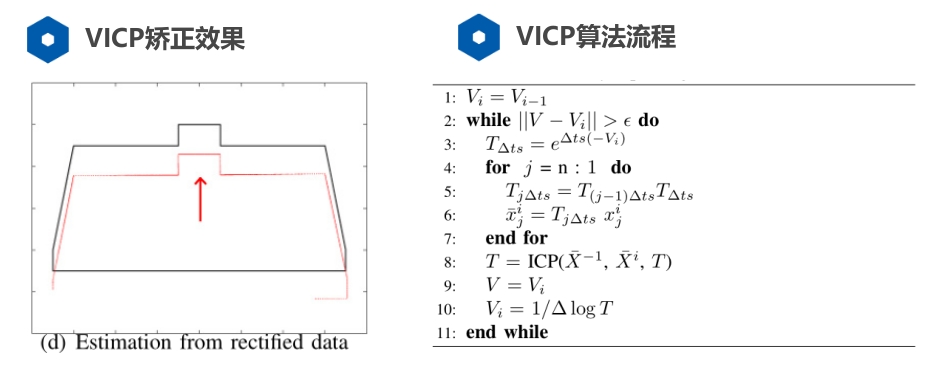
在 1.2、激光雷达运动畸变中，有个ICP矫正后的，通过对比，可以发现：VICP还是具有更好的效果的。
2.2、里程计辅助法(外部传感器辅助)
用IMU进行位姿估计，而不是雷达，IMU帧率足够高！
当然也可以使用其他传感器辅助去除Lidar运动畸变，例如：论速计
轮速计效果好一点。
任意时间点的位姿如果不能直接得到，可以通过插值得到，如下公式。
还可以进行二次多项式差值，懒得写了，简单，不多BB。
严格意义上，一帧点云中，每个点都应一个独特的机器人位姿，其对应的位姿都可以通过上述插值得到，这样就得到一帧矫正后的点云。
