Problem Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.
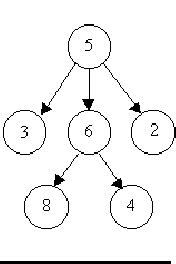
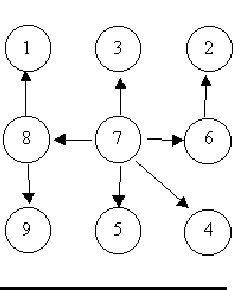
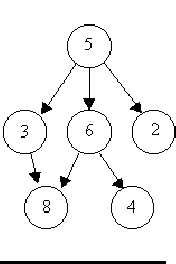
In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
There is exactly one node, called the root, to which no directed edges point.
Every node except the root has exactly one edge pointing to it.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not.



In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not.
Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero.
Output
For each test case display the line ``Case k is a tree." or the line ``Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1).
Sample Input
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1
Sample Output
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
题意很明确了就不解释了。之所以写这题,是因为同样的题目poj过了,hdu却没有过- -。。一直不知道是个什么原因,代码写的太弱了啊。后来看别人写的blog的思想
又写了一遍才a的。。这题时有向图,其中判断是否为树的条件有三:
 View Code
View Code
1. 肯定满足只有一个树根
2. 一个点不会被指向两次或两次以上。
3. 不能出现环
根据这个思想来写代码的话,就可以a了。。好囧
 View Code
View Code
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 const int N=1010; 6 int father[N],vis[N],degree[N]; 7 void init() 8 { 9 int i; 10 for(i=0;i<=N-10;i++) 11 { 12 father[i]=i; 13 vis[i]=0; 14 degree[i]=0; 15 } 16 } 17 int find(int x) 18 { 19 if(x!=father[x]) 20 father[x]=find(father[x]); 21 return father[x]; 22 } 23 int merge(int x,int y) 24 { 25 x=find(x),y=find(y); 26 if(x==y) return 0; 27 father[y]=x; 28 return 1; 29 } 30 int main() 31 { 32 int a,b,flag,maxx,cnt,i,cas=1; 33 while(scanf("%d%d",&a,&b)) 34 { 35 if(a<0||b<0) break; 36 printf("Case %d is ",cas++); 37 maxx=-1; 38 init(); 39 flag=1; 40 if(a==0&&b==0){printf("a tree.\n");continue;} 41 if(a>maxx) maxx=a; 42 if(b>maxx) maxx=b; 43 if(!merge(a,b)) flag=0; 44 vis[a]=vis[b]=1; 45 degree[b]++; 46 while(scanf("%d%d",&a,&b)&&(a+b)) 47 { 48 if(a>maxx) maxx=a; 49 if(b>maxx) maxx=b; 50 if(!merge(a,b))//此处判断是否出现环 51 flag=0; 52 vis[a]=vis[b]=1; 53 degree[b]++; 54 } 55 cnt=0; 56 for(i=1;i<=maxx&&flag;i++) 57 { 58 if(vis[i]&&father[i]==i) 59 cnt++; 60 if(cnt>1)//此处判断有几个根 61 flag=0; 62 if(degree[i]>1)//此处判断被指向几次 63 flag=0; 64 65 } 66 if(flag) printf("a tree.\n"); 67 else printf("not a tree.\n"); 68 } 69 return 0; 70 }
