粒子群优化算法

粒子群优化算法(Particle Swarm optimization,PSO)又翻译为粒子群算法、微粒群算法、或微粒群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。通常认为它是群集智能 (Swarm intelligence, SI) 的一种。它可以被纳入多主体优化系统(Multiagent Optimization System, MAOS)。粒子群优化算法是由Eberhart博士和kennedy博士发明。

场景假设

一群鸟随机的寻找食物，在这个区域里面只有一块食物，所有的鸟，都不知道食物在哪里，但他们都知道当前的位置距离食物还有多远，那么寻找到食物的最优策略是什么？

最简单有效的就是搜寻目前离食物最近的鸟的周围区域。

鸟群在整个搜寻的过程中，通过相互传递各自的信息，让其他的鸟知道自己的位置，通过这样的协作，来判断自己找到的是不是最优解，同时也将最优解的信息传递给整个鸟群，最终，整个鸟群都能聚集在食物源周围，即找到了最优解。

PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

基本原理

PSO初始化为一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解称为个体极值。另个一是整个种群目前找到的最优解，这个解称为全局极值。

算法定义

在n维连续搜索空间，对粒子群中的第i（1，2，3，…，m）进行定义。

如果每个粒子经历过的最优位置（pbest）记作

群体经历过的最优位置（gbest）记作

这样可以得到基本的POS算法为：

其中ω是惯性权重因子φ1,φ2是加速度常数，均为非负值。

rand(0,a1)和 rand(0,a2)为[0,a1]、[0,a2]范围内的具有均匀分布的随机数，a1与a2为相应的控制参数。

• 第一部分：是粒子在前一刻的速度；

• 第二部分：为个体“认知”分量，表示粒子本身的思考，将现有的位置和曾经经历过的最优位置相比。

• 第三部分：是群体“社会”分量，表示粒子间的信息共享和互相合作。
• φ1,φ2分别为控制个体认知分量和群体社会分量的相对贡献的学习率。
• 随机系数增加了搜索方向的随机性和算法的多样性。

PSO模型

• φ1 > 0, φ2 > 0; 为PSO全模型
• φ1 > 0, φ2 = 0; 为PSO认知模型
• φ1 = 0, φ2 > 0; 为PSO社会模型
• φ1 = 0, φ2 > 0 && g ≠ i; 为PSO无私模型

算法执行过程

1. 初始化每个粒子。在允许范围内随机设置每个粒子的初始位置和速度。
2. 评价每个粒子的适应度。计算每个粒子的目标函数。
3. 设置每个粒子的Pi。对于每个粒子，将其适应度与其经历的最好位置Pi进行比较，维持Pi最优。
4. 设置全局最优值Pg。对于每个粒子，将其适应度与群体经历的最好位置Pg进行比较，位置Pg最优。
5. 更新粒子的速度和位置。通过上面的公式。
6. 检查终止条件。没有达到预设条件则重新从第二步开始。

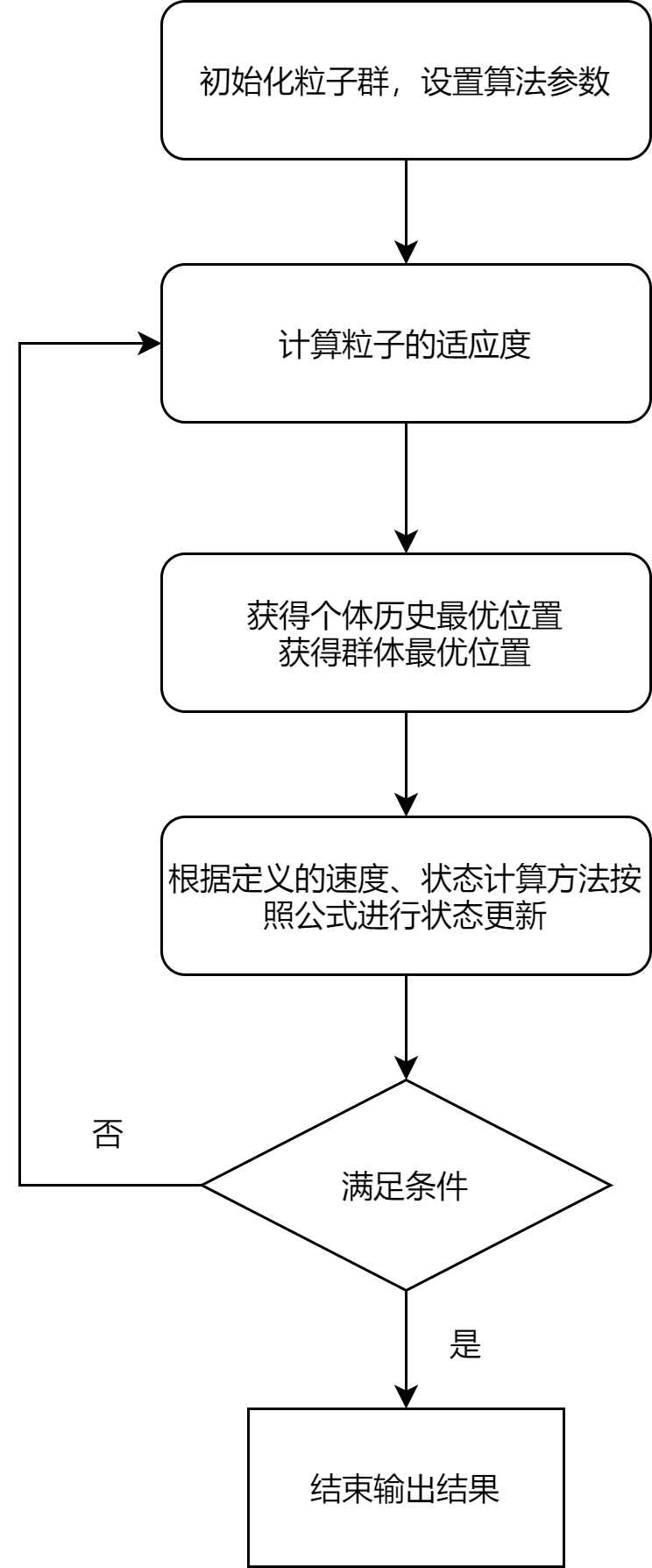
算法流程图