
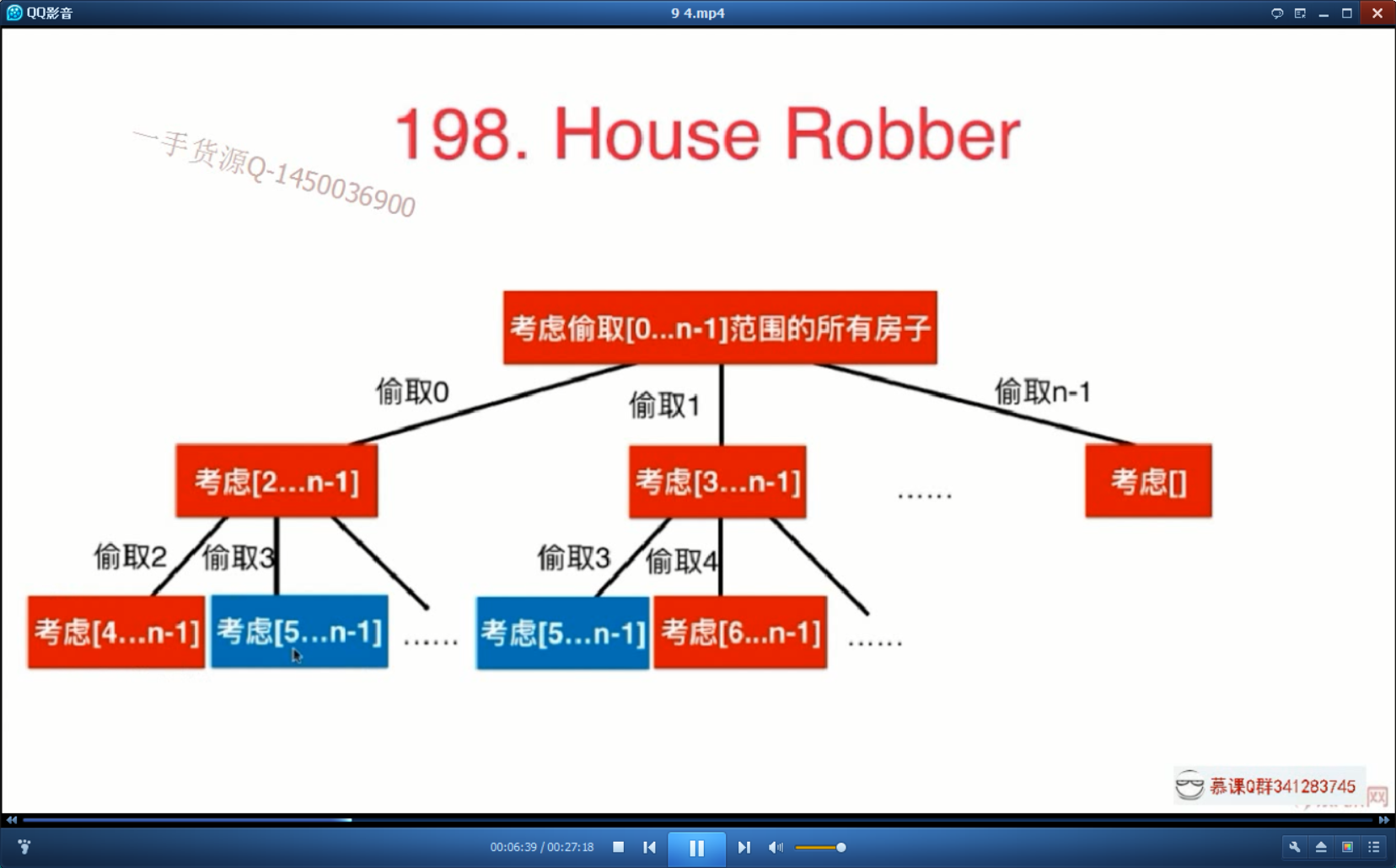
这个是上图的表达式

一个动态规划问题,最重要的就是他的状态转移方程。
递归实现

记忆化搜索

动态规划
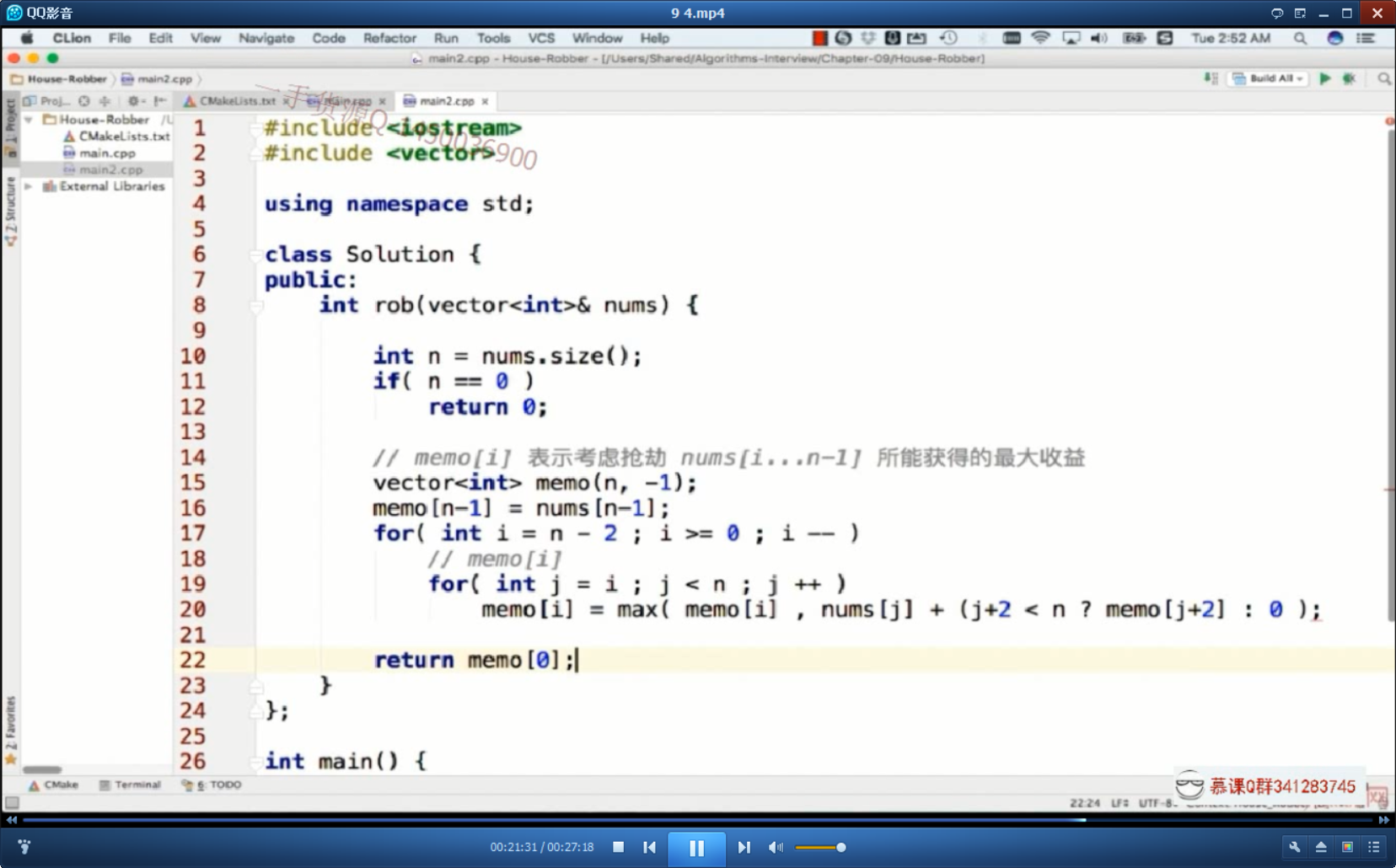
不同的状态,解法也是不同的

视频里的状态转移有点过于复杂,我也想到了另一种方法,也AC了。
也侧面反映了,状态转移方程的不同,可以一提多解。

就是选第一个,和不选第一个,这样方程更简洁更好懂。
public static int memo[]; public static int robber(int[] nums,int begin){ int len = nums.length; //这个递归要三个及三个元素以上才成立 //别计算nums的长度。。。因为肯定是一样的 //如果还有一个元素,begin是最后一个元素 if(begin==len-1) return nums[begin]; //begin,begin+1,两个元素 if(begin==len-2){ return nums[begin]>nums[begin+1]?nums[begin]:nums[begin+1]; } if(begin>=len-2) return nums[begin]; if(memo[begin]!=-1) return memo[begin]; //选第一个和后面的 int state1 = nums[begin]+robber(nums,begin+2); //不选第一个,直接选后面的 int state2 = robber(nums,begin+1); if(state1>state2) memo[begin]=state1; else memo[begin]=state2; return memo[begin]; } public int rob(int[] nums) { int len = nums.length; if (len==0) return 0; memo = new int [len]; for(int i=0;i<len;i++) memo[i]=-1; return robber(nums,0); }

还是犯了很多错误啊。。。。。
213
337
309