学习的速度有些慢,脑袋转动的频率有些不是很高。不过今天的效率我觉得还是可以,应该不能称效率吧,就是整个感觉不错,感觉自己补充了很多的知识。其实G家和F家败了之后不知道看看算法题对接下来的找工作帮助是否会很大,但是看算法题目也是提高解决问题能力的一种方式吧,锻炼思维。僵化的思维实在有些不能忍受。
另外今天更是遇到之前leetcode之中的一些题目,当时那个题目第一时间没有思路,想了良久有了思路,有种灵机一动的感觉,今天碰到的时候竟然没有回想起来,即使自己的灵机一闪也无法依赖。那种灵机一动的时候人的状态可能提升了,正常的状态没办法恢复到那个效果了-_-。也许不断提高自己的正常状态,或者增加灵机一动的几率,也许只有靠不断的锻炼和不断的温故而知新了~。废话这么多,直接进入正题吧,今天的题目当中还是有很多非常值得期待(百思不得其解)的题目。
1.荷兰国旗问题。朴素的解释就是只含有0,1,2的数组进行排序,要求时间复杂度O(n),空间复杂度O(1)。(Leetcode)
扩展问题:如果数组含有0,1,2,3四个数值进行排序又需要如何排序?
类似快速排序的partition,但是快排的partition过程关于相等的部分未进行处理。思路就是保持一个尾部其后方均大于partition元素,保持一个头部指针其前方均小于partition元素。中间自然就是等于partition的元素。
void sorted(int A[],int i) {
//quick sort partition is not right
int start = 0;
int end = Alen - 1;
int partition = A[i];
for(int i = start;i <= end;i++) {
if( A[i] == partition ) {
continue;
}
else if( A[i] > partition ) {
swap(A[i--],A[end--]);
}
else {
swap(A[i--],A[start++]);
}
}
}
关于扩展问题4个元素的排序,我的想法是首先利用第二个数利用上述的方法进行partition会得到一个相对有序的数组,但是end -- 数据结尾这部分未排序,包含后两个元素的乱序,重新在进行一下partition,即调用两次partition的过程应该可以完成任务。不知道是不是还有更好的思路,欢迎留言~
2.设计一个方法,读&写一个未初始化的数组可达到O(1)的时间复杂度,可以利用额外的O(n)的空间,如果读到未初始化的单元需要返回false。
这个题目在《编程珠玑》中也出现过,但是只是简单的描述下思路,没有理解这个解题的过程,趁这个时间了解到了这个解题过程,非常有技巧的一个方法。
首先想到的利用额外的数组标示是否初始化...但是却被额外的数组如何初始化困扰-_-。 好吧,自己确实想不出什么好办法。
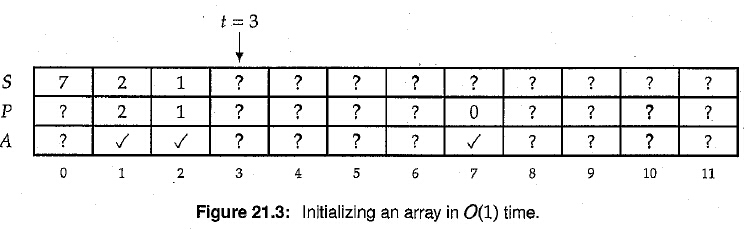
解决方案额外引入O(2n)的空间和一个整型变量。 思路如下图所示~
初始化操作:t=0,需要O(1)的时间复杂度。辅助数组P,S均是未初始化。
判断A[i]是否初始化利用:P[i] < t && S[P[i]] == i ( 可以这么理解,如果第i个未初始化,则P[i]随机数。如果不在0-t之间,直接返回未初始化。如果刚好是0-t的随机数,但是S[P[i]] == i这个随机数又无法保证,所以这里就能得出未初始化的结论)
插入一个元素的时候将P[i]对应的地方写入t,S[t] = i,然后t++,就能一直保证上面的验证了~。
图例表示的首先插入7,然后插入2,然后插入1后的状态。
3.一个数组A,求满足i < j的情况下,max(A[j] - A[i]),时间复杂度O(n)。
扩展问题:求满足 i 0 < j 0 < i 1 < j 1 的情况下,max( A[j0] - A[i0] + A[j1] - A[i1] ),时间复杂度O(n)。
更复杂的扩展问题:如果将上面的问题,1,2,扩展至n又应该如何解题目?即 max(A[j0] - A[i0] + A[j1] - A[i1] + .... + A[jk-1] - A[ik-1])。如何解决该普适性的问题呢?
这些题目刚好对应leetcode中的 股票I II III三个问题,其中更复杂的扩展为普适性解法。
4.设计一个高效的求n-sum子集模0的问题。问题具体描述,给定一个数组A,数组A的长度为n,设计一个高效的方法求出数组中模n为0的子集。
题目意思比较理解,当时没有理解透彻,以为和leetcode中的2-sum On,3-sum On2,4-sum On3 是一个类型的问题。所以就没有仔细思考。
解题思路如下:预先处理数组A,计算出prefixsum[i]为从0-i的A数组的和,根据i可以从0-n-1的属性,一共有n个前缀和,模n的结果为0-n-1刚好也n个鸽子,如果n个鸽子放进n个笼子,只有两种结果,每个笼子都有鸽子或是一个笼子放进了至少两个鸽子,如果第一种情况,则模为0的结果直接返回。 如果是一个笼子至少放进了两个鸽子,则可知prefixsum[x] == prefixsum[y],且假设x < y,则x 至 y 这段的和为0,模为0的和返回即可。~
题目中还有鸽巢原理的意味。
5.设计一个求出数组A中最长连续递增子串的算法。
理解题意之后就是连续增长的子串,扫描一遍就可以得到了,保存一个最长的长度,和最长长度开始的位置,扫描完毕直接截取子串就可以了。
EPI中描述了一种稍微优化的方法,稍微优化是因为最快情况的时间复杂度依然是O(n),这样相比之前,常数时间内没有得到提高。而且平均时间复杂度不像快速排序那样容易分析,不过优化的思路还是很有技巧的。
假设遍历中的一个场景,遍历至数组A[i]得到A[i-1]>=A[i],依照之前暴力的方法,这里需要在A[i]的位置重新开始计算一个子数组。这里假设在A[i]之前已经找到一个最长长度为L的连续递增子串,此时可以直接从A[i+L]的位置向A[i]遍历,如果出现一次非递减的数对,可以直接将i的位置调整至这个非递减的位置。
6.题目描述有些长,看起来是一个非常像考查并查集的题目。
并查集数据结构如何实现呢?
7.题意没有理解透彻,所以先不更新上来。
8.利用字符串模拟高精度的大整数乘法。
算是一个比较基础的题目了,实现的时候注意细节,如果利用string的话因为每个char的上限是255,实现乘法的时候我一般利用的是vector<int>这样没有一个溢出的问题。
9.给出一个数组A,和一个针对数组A的置换,利用常数的空间复杂度完成该置换对数组A的操作。
非常数空间复杂度的计算非常容易,重新开辟一个数组A,针对每个置换的位置直接将A的元素放置在置换后的位置即可。
置换可以分为不同的环,不同的环进行一次置换的时候不需要空间复杂度。但是分环的过程呢?其实这个问题在O(1)进行置换的时候存在一个问题是无法知道停止条件,这里有一个特殊的小技巧,每次利用完一个置换元素置换之后,将其减去置换数组的长度,这样它就变成了负数,再遇到这个时你就能够了解到它已经被访问过了。事后再将这些元素还原即可。
10.利用常数空间复杂度求一个置换的逆。
思路和上面题目的技巧类似,
11.求排列的下一个排列,及实现next_permutation。
扩展问题:求n个数字排列的第k个排列。
扩展问题:求排列的前一个排列,及实现pre_permutation.
组合数学中的一个很常见的算法~
第一个扩展问题,可以首先利用dfs求取全排列的模板,统计到k的时候完成,但是这样效率比较低,所以可以利用实现存储好的阶乘表进行剪枝操作,不断的剪去无效的搜索。
12.针对字符串进行原地的循环移位。
进行3次reverse操作即可完成操作。
13.将一个正方形矩阵旋转90度操作。
a.首先最直观的思路就是单个元素单个元素的进行置换。一层一层的向里进行,代码有些类似矩形的螺旋输出算法。
b.可以进行两次反转完成旋转90度的操作。如下图:
