衡量回归算法的标准
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets
波士顿房产数据
boston = datasets.load_boston()
x = boston.data[:, 5] # 只使用房间数量这个特征
x.shape
(506,)
y = boston.target
y.shape
(506,)
plt.scatter(x, y)
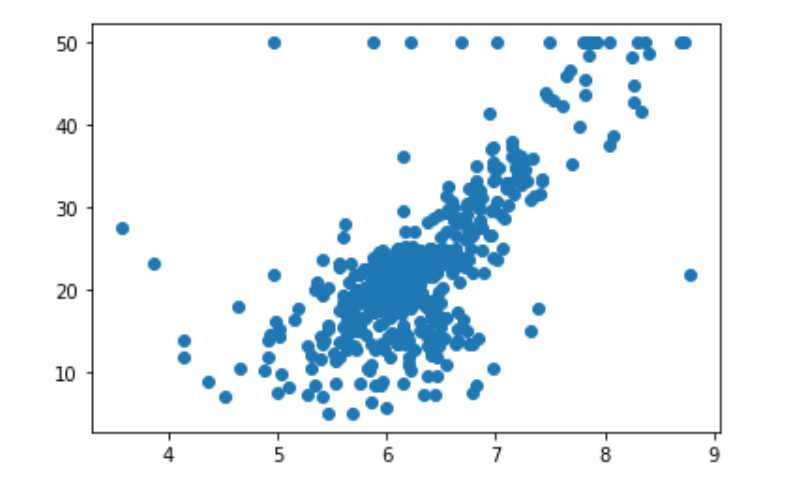
np.max(y)
50.0
去除干扰数据
x = x[y < 50.0] y = y[y < 50.0] x.shape, y.shape
((490,), (490,))
plt.scatter(x, y)
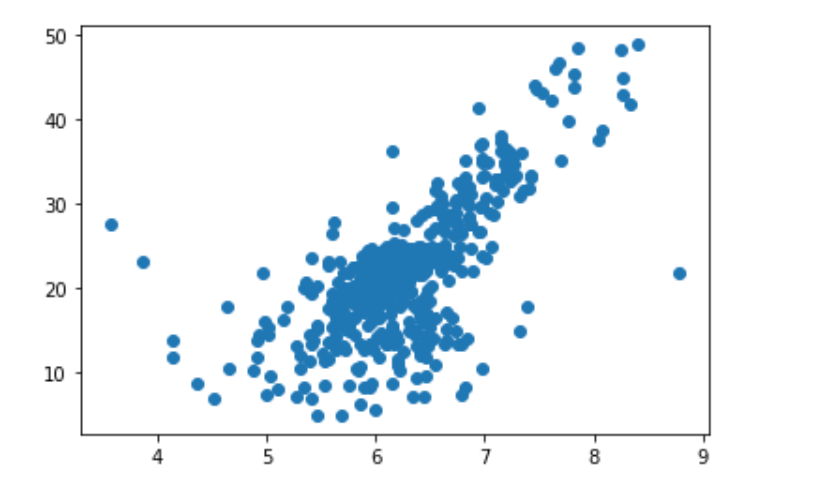
使用简单线性回归
# 数据分割为训练集和测试集 from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=666)
x_train.shape, y_train.shape
((367,), (367,))
# 使用训练集求归回方程 x_mean = np.mean(x_train) y_mean = np.mean(y_train) num = (x_train - x_mean).dot(y_train - y_mean) d = (x_train - x_mean).dot(x_train - x_mean) a = num / d b = y_mean - a * x_mean y_hat = a * x_train + b
x_train.shape, y_train.shape
((367,), (367,))
y_hat.shape
(367,)
plt.scatter(x_train, y_train)
plt.plot(x_train, y_hat)

衡量回归算法的标准
# 在回归方程下求测试集的预测值 y_predict = a * x_test + b
# MSE 预测值与真实值误差衡量 mse_test = np.sum((y_predict - y_test)**2) / len(y_test) mse_test
28.215949368640807
# RMSE from math import sqrt rmse_test = sqrt(mse_test) rmse_test
5.311868726600913
# MAE mae_test = np.sum(np.absolute(y_predict - y_test)) / len(y_test) mae_test
3.9489046062737834
sklearn 中的MSE MAE
from sklearn.metrics import mean_squared_error from sklearn.metrics import mean_absolute_error
mean_squared_error(y_test, y_predict)
28.215949368640807
mean_absolute_error(y_test, y_predict)
3.9489046062737834
R Square
rsquare = 1 - mean_squared_error(y_test, y_predict) / np.var(y_test)
rsquare
0.5682464825049472
from sklearn.metrics import r2_score r2_score(y_test, y_predict)
0.5682464825049472