DFT(Discrete Fourier Transform):离散傅立叶变换
直观的计算DFT算法复杂度为O(N*N)。
FFT(Fast Fourier Transformation):快速傅立叶变换,DFT的快速算法。凡将DFT算法复杂度降至O(N*logN)的算法,均可称为FFT。
最常用的FFT为奇偶分治法,要求输入点个数N为2的幂。下文中均假设N为2的幂。
N个点的DFT处理器定义:
N个点的DFT处理器有N个输入和N个输出,输入N个点的值,输出各点的变换结果值。
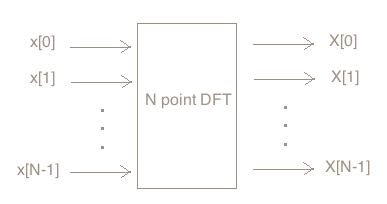 (注意左边x为小写,右边X为大写)
(注意左边x为小写,右边X为大写)
黑箱内逻辑为:
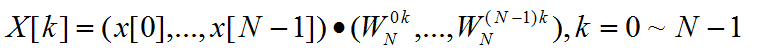
其中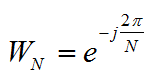 。
。
根据N个点的DFT处理器的定义,可以推得N/2个点的DFT处理器的定义。
N/2个点的DFT处理器定义:
N/2个点的DFT处理器有N/2个输入和N/2个输出,输入N/2个点的值,输出各点的变换结果值。

黑箱内逻辑为:
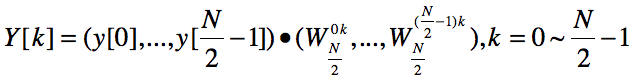
考虑下面问题:
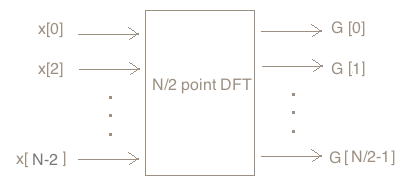
问题一:将N/2个偶点x[0],x[2],x[4],...,x[N-2]输入N/2个点的DFT处理器,设输出为G[0],G[1],...,G[N/2-1],那么G[k](k=1~N/2-1)等于多少?
解:根据N/2个点的DFT处理器定义,得:
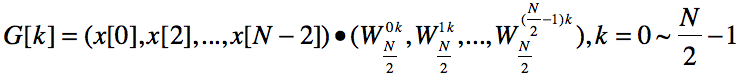
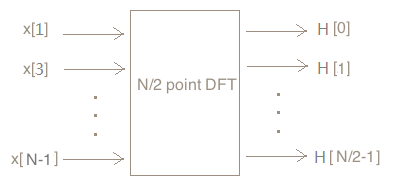
问题二:将N/2个奇点x[1],x[3],x[5],...,x[N-1]输入N/2个点的DFT处理器,设输出为H[0],H[1],...,H[N/2-1],那么H[k](k=1~N/2-1)等于多少?
解:根据N/2个点的DFT处理器定义,得
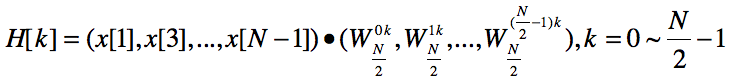
考虑下面问题:
假设我现在想计算N个点x[0]~x[N-1]的DFT的结果X[0]~X[N-1],但是凑巧学前班没毕业不会算数儿,所以只能借助一个现成的N个点的DFT处理器来完成计算,但凑巧手头没有N个点的DFT处理器,却凑巧有两个N/2个点的DFT处理器,那么我还能不能完成计算呢?
解:
能完成计算,可以用两个N/2个点的DFT处理器DIY一个N个点的DFT处理器,然后用这个DIY的DFT处理器完成计算。
那么,如何DIY呢?
首先可验证恒等式:
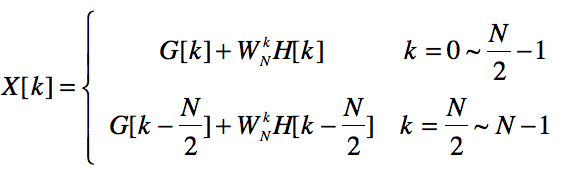
然后据此恒等式连电路,连好结果如下:
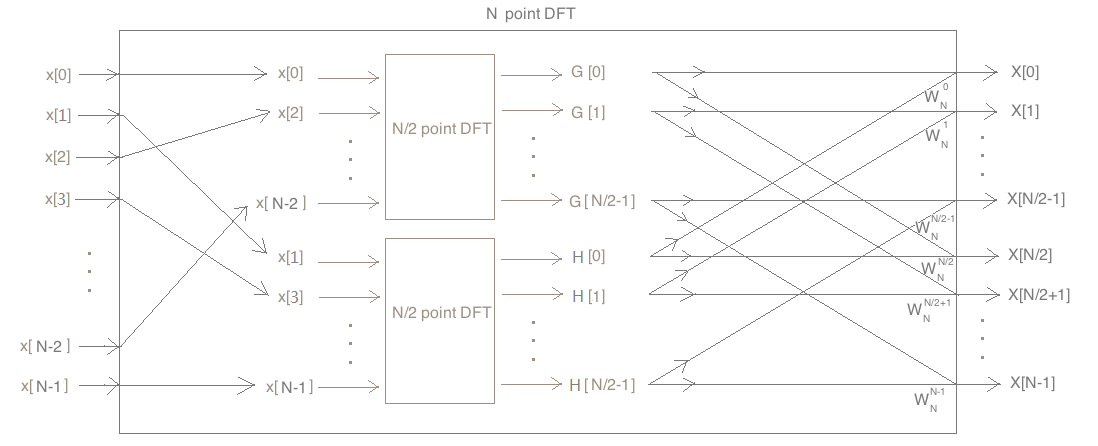
由此可见,可以用两个N/2个点的DFT处理器组装成N个点的DFT处理器。重复这一思想,那两个N/2个点的DFT处理器每个都可以由两个N/4个点的DFT处理器组成,由于N为2的幂,所以此过程可反复进行,直到分解为1个点的DFT处理器为止。
此即基于奇偶分治的FFT算法。
算法复杂度分析:
设使用上述FFT算法的情况下N point DFT所需乘法次数为C(N),则根据上面电路图显然有:
C(N)=2C(N/2)+N
又由于1个点的FFT所需乘法次数为1(即输入值x乘以![]() ),即
),即
C(1)=1
求解此递推公式,得
![]()
所以算法复杂度为O(N*logN)
参考:
https://www.youtube.com/watch?v=EsJGuI7e_ZQ
https://www.youtube.com/watch?v=1mVbZLHLaf0
----补充
一,
因为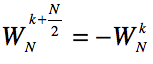 ,所以前面电路图可等价地优化为:
,所以前面电路图可等价地优化为:
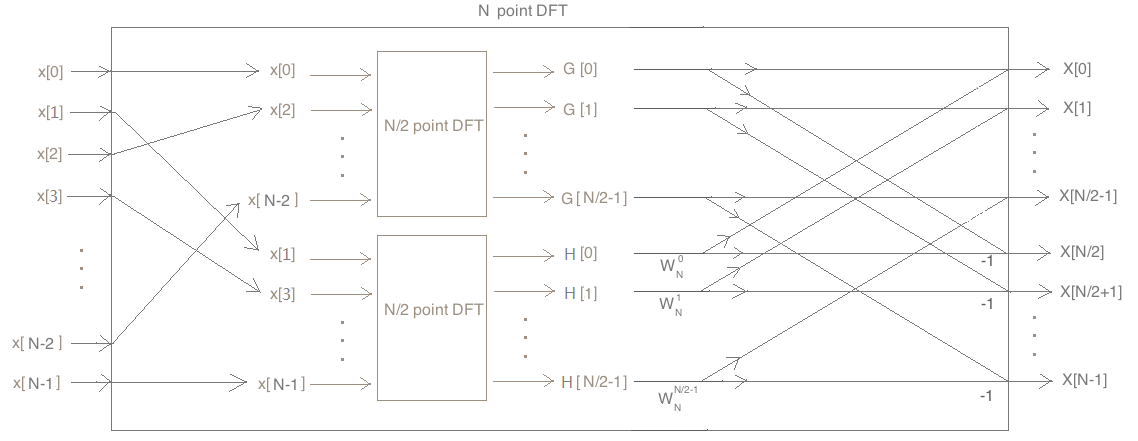
参考:https://cnx.org/contents/zmcmahhR@7/Decimation-in-time-DIT-Radix-2 (其中Additional Simplification一节)。
二,
递推公式
C(N)=2C(N/2)+N
C(1)=1
求解过程如下:
令
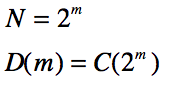
则
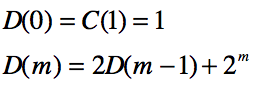
用累加法求解D(m),写:
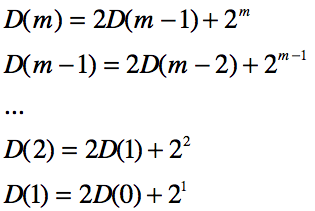
将第二式乘以2,将第三式乘以4,将第四式乘以8...然后累加,得:
![]()
所以
![]()
即
![]()