关于多分类
我们常见的逻辑回归、SVM等常用于解决二分类问题，对于多分类问题，比如识别手写数字，它就需要10个分类，同样也可以用逻辑回归或SVM，只是需要多个二分类来组成多分类，但这里讨论另外一种方式来解决多分类——SoftMax。
SoftMax模型
Softmax回归模型是logistic回归模型在多分类问题上的推广，当分类数为2的时候会退化为Logistic分类。.在多分类问题中，类标签 可以取两个以上的值。 Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的，该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的。
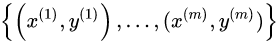，，由于logistic回归是针对二分类问题的，因此类标记 。
假设函数如下：
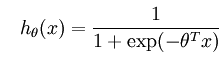
训练模型参数 ，使其能够最小化代价函数：
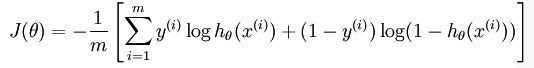
对于给定的测试输入 ，用假设函数针对每一个类别
估算出概率值
，即，估计
的每一种分类结果出现的概率。假设函数将要输出 一个
维的向量来表示这
个估计的概率值。假设函数
形式如下：
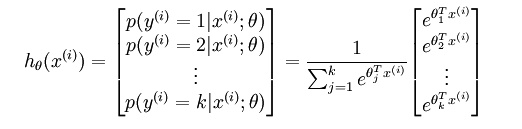
代价函数
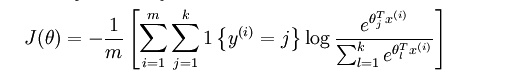
上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为：
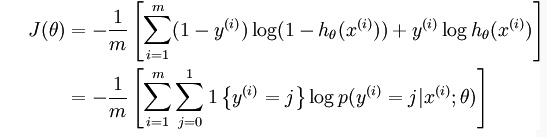
Softmax代价函数与logistic 代价函数在形式上非常类似，只是在Softmax损失函数中对类标记的 个可能值进行了累加。注意在Softmax回归中将
分类为类别
的概率为：
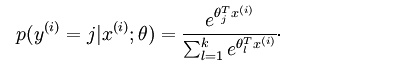
一般使用梯度下降优化算法来最小化代价函数，而其中会涉及到偏导数，即，则对求偏导，得到代价函数对参数权重的梯度就可以优化了。
例子
从下图看，神经网络中包含了输入层，然后通过两个特征层处理，最后通过softmax分析器就能得到不同条件下的概率，这里需要分成三个类别，最终会得到y=0、y=1、y=2的概率值。
继续看下面的图，三个输入通过softmax后得到一个数组[0.05 , 0.10 , 0.85]，这就是soft的功能。
计算过程直接看下图，其中即为，三个输入的值分别为3、1、-3，的值为20、2.7、0.05，再分别除以累加和得到最终的概率值，0.88、0.12、0。
可以看到它有多个值，所有值加起来刚好等于1，每个输出都映射到了0到1区间，可以看成是概率问题。
为多个输入，训练其实就是为了逼近最佳的。
使用场景
在多分类场景中可以用softmax也可以用多个二分类器组合成多分类，比如多个逻辑分类器或SVM分类器等等。该使用softmax还是组合分类器，主要看分类的类别是否互斥，如果互斥则用softmax，如果不是互斥的则使用组合分类器。
参考文献：
https://www.cnblogs.com/hellcat/p/7220536.html?utm_source=itdadao&utm_medium=referral