Logistic回归
Logistic回归的一般过程
(1)收集数据:采用任意方法收集数据
(2)准备数据:由于需要进行距离计算,因此要求数据类型为数值型。另外,结构化数据格式最佳
(3)分析数据:采用任意方法对数据进行分析
(4)训练算法:大部分时间用于训练,训练的目的是为了找到最佳的分类回归系数
(5)测试算法:一旦训练步骤完成,分类将会很快
(6)使用算法:首先,我们需要输入一些数据,并将其转化成对应的结构化数值;接着,基于训练好的回归系数就可以对这些数值进行
简单的回归计算,判定他们属于哪个类别;在这之后,我们就可以在输出的类别上做一些其他的分析工作
Logistic回归的优缺点
优点:计算代价不高,易于理解和实现
缺点:容易欠拟合,分类精度可能不高
适用数据类型:数值型和标称型数据
Sigmoid函数的计算公式:

1 import os 2 os.getcwd() 3 os.chdir('F:machine_learninglogistic回归') 4 5 #加载数据集 6 def loadDataSet(): 7 dataMat=[]#用于存放数据集 8 labelMat=[]#用于存放标签集 9 fr=open('test.txt','r')#打开测试数据集 10 for line in fr.readlines():#逐行读取 11 lineArr=line.strip().split(' ')#将数据集按照标准格式划分 12 dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])#在dataMat中添加数据集 13 labelMat.append(lineArr[2])#在labelMat中添加标签数据 14 return dataMat,labelMat 15 16 dataMat,labelMat=loadDataSet() 17 18 from math import exp 19 from math import log 20 #建立sigmoid函数 21 def sigmoid(inX): 22 return 1/(1+exp(-inX))#返回sigmoid函数值 23 from numpy import * 24 #Logistic回归梯度上升优化算法 25 def stocGradAscent0(dataMatrix,classLabels): 26 dataMatrix=array(dataMatrix) 27 m,n=shape(dataMatrix)#计算数据集的行和列 28 classLabels=array(classLabels).astype('float64') 29 alpha=0.01#阈值设定为0.01 30 weights=ones(n)#初始化权重矩阵 31 for i in range(m): 32 h=sigmoid(sum(dataMatrix[i]*weights))#计算在sigmoid函数作用下的标签值 33 error=classLabels[i]-h#计算误差 34 weights=weights+alpha*(error*dataMatrix[i].transpose())#更新权重 35 return weights.tolist() 36 weights=stocGradAscent0(dataMat,labelMat)

1 import matplotlib.pyplot as plt 2 plt.rcParams['font.sans-serif']=['SimHei']#解决中文显示问题 3 plt.rcParams['axes.unicode_minus']=False#解决中文显示问题 4 def plotBestFit(weights): 5 dataMat,labelMat=loadDataSet()#加载数据集 6 dataArr=mat(dataMat)#将数据集转化成矩阵 7 n=shape(dataMat)[0]#求出数据集的行数 8 xcord1=[];ycord1=[]#用于存放标签是1的数据集 9 xcord2=[];ycord2=[]#用于存放标签是2的数据集 10 for i in range(n): 11 if int(labelMat[i])==1: 12 xcord1.append(dataArr[i,1])#将标签是1对应的x1的值存放在xcord1中 13 ycord1.append(dataArr[i,2])#将标签是2对应的x2的值存放在ycord1中 14 elif int(labelMat[i])==0: 15 xcord2.append(dataArr[i,1]) 16 ycord2.append(dataArr[i,2]) 17 fig=plt.figure() 18 ax=fig.add_subplot(111) 19 ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')#绘制对应数据集是1的点,s代表点的大小,c代表颜色,marker代表线型,默认是原型 20 ax.scatter(xcord2,ycord2,s=30,c='green') 21 x=arange(-3.0,3.0,0.1) 22 y=(-weights[0]-weights[1]*x)/weights[2]#线性方程y=ax+b 23 ax.plot(x,y) 24 plt.xlabel('X1') 25 plt.ylabel('Y1') 26 plt.show() 27 plotBestFit(weights)
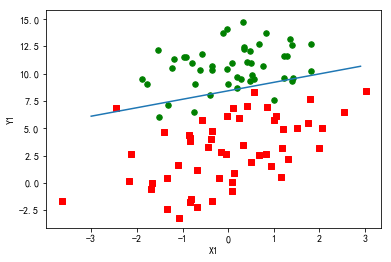
得出的最佳拟合直线如图:

1 #改进的随机梯度上升法 2 def stocGradAscent1(dataMatrix, classLabels, numIter=150): 3 dataMatrix=array(dataMatrix) 4 m,n = shape((dataMatrix)) 5 weights =ones(n) #initialize to all ones 6 classLabels=array(classLabels).astype('float64') 7 for j in range(numIter): 8 dataIndex = range(m) 9 for i in range(m): 10 alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not 11 randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant 12 h = sigmoid(sum(dataMatrix[randIndex]*weights)) 13 error = classLabels[randIndex] - h 14 weights = weights + alpha *error *(dataMatrix[randIndex].transpose()) 15 # del(dataIndex[randIndex]) 16 return weights.tolist() 17 weights=stocGradAscent1(dataMat,labelMat)
示例:从疝气病症预测病马的死亡率

1 ###预测算法,用Logistic回归进行分类 2 def ClassifyVector(inX,weights): 3 prob=sigmoid(sum(inX*weights))#计算在sigmoid函数作用下的函数值 4 if prob>0.5:return 1 5 else:return 0 6 7 8 #计算错误率 9 def colicTest(): 10 frtrain=open('horseColicTraining.txt')#打开训练数据集 11 frtest=open('horseColicTest.txt')#打开测试数据集 12 trainingSet=[]#用于存放训练数据集 13 trainingLabels=[]#用于存放标签数据集 14 for line in frtrain.readlines(): 15 currLine=line.strip().split(' ')#将每行数据以四个空格分割 16 lineArr=[] 17 for i in range(21):#共有20个特征,1个类别数据 18 lineArr.append(float(currLine[i])) 19 trainingSet.append(lineArr) 20 trainingLabels.append(float(currLine[21])) 21 trainWeights=stocGradAscent1(trainingSet,trainingLabels)#求出训练数据的权重 22 errorCount=0.0;numTestVec=0.0#记初始错误数据为0个 23 for line in frtest.readlines(): 24 numTestVec+=1 25 currLine=line.strip().split(' ') 26 lineArr=[] 27 for i in range(21): 28 lineArr.append(float(currLine[i])) 29 if int(ClassifyVector(array(lineArr),trainWeights))!=int(currLine[21]): 30 errorCount+=1 31 errorRate=(float(errorCount))/numTestVec 32 print('错误率为:%f'%(errorRate)) 33 return errorRate 34 #errorRate=colicTest() 35 def multiTest1(): 36 errorSum=0;numTests=10 37 for i in range(10): 38 errorSum+=colicTest() 39 print('average rate ratio is:%f'%(errorSum/float(numTests)))
结果如下:
错误率为:0.313433
错误率为:0.328358
错误率为:0.417910
错误率为:0.298507
错误率为:0.283582
错误率为:0.283582
错误率为:0.298507
错误率为:0.253731
错误率为:0.283582
错误率为:0.313433
average rate ratio is:0.307463
全部代码
1 # -*- coding: utf-8 -*- 2 """ 3 Created on Fri May 11 18:51:10 2018 4 5 @author: wangmengzhu 6 """ 7 8 '''logistic回归''' 9 10 import os 11 os.getcwd() 12 os.chdir('F:machine_learninglogistic回归') 13 14 #加载数据集 15 def loadDataSet(): 16 dataMat=[]#用于存放数据集 17 labelMat=[]#用于存放标签集 18 fr=open('test.txt','r')#打开测试数据集 19 for line in fr.readlines():#逐行读取 20 lineArr=line.strip().split(' ')#将数据集按照标准格式划分 21 dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])#在dataMat中添加数据集 22 labelMat.append(lineArr[2])#在labelMat中添加标签数据 23 return dataMat,labelMat 24 25 dataMat,labelMat=loadDataSet() 26 27 from math import exp 28 from math import log 29 #建立sigmoid函数 30 def sigmoid(inX): 31 return 1/(1+exp(-inX))#返回sigmoid函数值 32 from numpy import * 33 #Logistic回归梯度上升优化算法 34 def stocGradAscent0(dataMatrix,classLabels): 35 dataMatrix=array(dataMatrix) 36 m,n=shape(dataMatrix)#计算数据集的行和列 37 classLabels=array(classLabels).astype('float64') 38 alpha=0.01#阈值设定为0.01 39 weights=ones(n)#初始化权重矩阵 40 for i in range(m): 41 h=sigmoid(sum(dataMatrix[i]*weights))#计算在sigmoid函数作用下的标签值 42 error=classLabels[i]-h#计算误差 43 weights=weights+alpha*(error*dataMatrix[i].transpose())#更新权重 44 return weights.tolist() 45 weights=stocGradAscent0(dataMat,labelMat) 46 47 48 #改进的随机梯度上升法 49 def stocGradAscent1(dataMatrix, classLabels, numIter=150): 50 dataMatrix=array(dataMatrix) 51 m,n = shape((dataMatrix)) 52 weights =ones(n) #initialize to all ones 53 classLabels=array(classLabels).astype('float64') 54 for j in range(numIter): 55 dataIndex = range(m) 56 for i in range(m): 57 alpha = 4/(1.0+j+i)+0.0001 #apha decreases with iteration, does not 58 randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constant 59 h = sigmoid(sum(dataMatrix[randIndex]*weights)) 60 error = classLabels[randIndex] - h 61 weights = weights + alpha *error *(dataMatrix[randIndex].transpose()) 62 # del(dataIndex[randIndex]) 63 return weights.tolist() 64 weights=stocGradAscent1(dataMat,labelMat) 65 #画出数据集和Logistic回归最佳拟合直线的函数 66 import matplotlib.pyplot as plt 67 plt.rcParams['font.sans-serif']=['SimHei']#解决中文显示问题 68 plt.rcParams['axes.unicode_minus']=False#解决中文显示问题 69 def plotBestFit(weights): 70 dataMat,labelMat=loadDataSet()#加载数据集 71 dataArr=mat(dataMat)#将数据集转化成矩阵 72 n=shape(dataMat)[0]#求出数据集的行数 73 xcord1=[];ycord1=[]#用于存放标签是1的数据集 74 xcord2=[];ycord2=[]#用于存放标签是2的数据集 75 for i in range(n): 76 if int(labelMat[i])==1: 77 xcord1.append(dataArr[i,1])#将标签是1对应的x1的值存放在xcord1中 78 ycord1.append(dataArr[i,2])#将标签是2对应的x2的值存放在ycord1中 79 elif int(labelMat[i])==0: 80 xcord2.append(dataArr[i,1]) 81 ycord2.append(dataArr[i,2]) 82 fig=plt.figure() 83 ax=fig.add_subplot(111) 84 ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')#绘制对应数据集是1的点,s代表点的大小,c代表颜色,marker代表线型,默认是原型 85 ax.scatter(xcord2,ycord2,s=30,c='green') 86 x=arange(-3.0,3.0,0.1) 87 y=(-weights[0]-weights[1]*x)/weights[2]#线性方程y=ax+b 88 ax.plot(x,y) 89 plt.xlabel('X1') 90 plt.ylabel('Y1') 91 plt.show() 92 plotBestFit(weights) 93 94 95 96 ###预测算法,用Logistic回归进行分类 97 def ClassifyVector(inX,weights): 98 prob=sigmoid(sum(inX*weights))#计算在sigmoid函数作用下的函数值 99 if prob>0.5:return 1 100 else:return 0 101 102 103 #计算错误率 104 def colicTest(): 105 frtrain=open('horseColicTraining.txt')#打开训练数据集 106 frtest=open('horseColicTest.txt')#打开测试数据集 107 trainingSet=[]#用于存放训练数据集 108 trainingLabels=[]#用于存放标签数据集 109 for line in frtrain.readlines(): 110 currLine=line.strip().split(' ')#将每行数据以四个空格分割 111 lineArr=[] 112 for i in range(21):#共有20个特征,1个类别数据 113 lineArr.append(float(currLine[i])) 114 trainingSet.append(lineArr) 115 trainingLabels.append(float(currLine[21])) 116 trainWeights=stocGradAscent1(trainingSet,trainingLabels)#求出训练数据的权重 117 errorCount=0.0;numTestVec=0.0#记初始错误数据为0个 118 for line in frtest.readlines(): 119 numTestVec+=1 120 currLine=line.strip().split(' ') 121 lineArr=[] 122 for i in range(21): 123 lineArr.append(float(currLine[i])) 124 if int(ClassifyVector(array(lineArr),trainWeights))!=int(currLine[21]): 125 errorCount+=1 126 errorRate=(float(errorCount))/numTestVec 127 print('错误率为:%f'%(errorRate)) 128 return errorRate 129 #errorRate=colicTest() 130 def multiTest1(): 131 errorSum=0;numTests=10 132 for i in range(10): 133 errorSum+=colicTest() 134 print('average rate ratio is:%f'%(errorSum/float(numTests)))
