【剑指offer】11--旋转数组的最小数字（二分查找）

原创博文，转载请注明出处！

# 本文是牛客网《剑指offer》刷题笔记

1.题目

     旋转数组的最小数字：输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。

     注意：给出的所有元素都大于0，若数组大小为0，请返回0。

2.思路

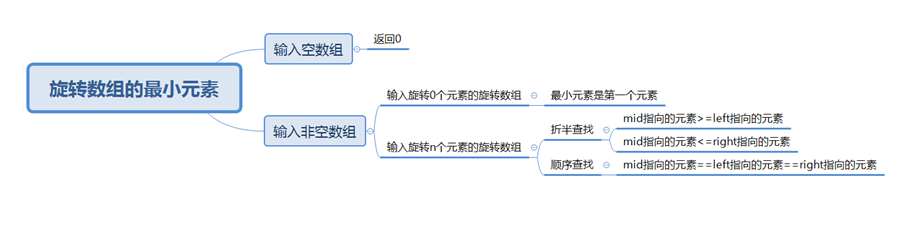
• 空数组查找最小元素：      

        输出0

• 非空数组查找最小元素：

# 如果输入旋转0个元素的旋转数组，则第一个元素即最小元素     

# 如果输入旋转n个元素的旋转数组，则按二分查找和顺序查找的思路查找最小元素

二分查找过程：

        旋转数组特性：旋转数组将原有序数组分成递增子数组1和递增子数组2，递增子数组1的元素>=递增子数组2，最小元素是两个子数组的分界线。设置辅助变量：指针left指向旋转数组的第一个元素；指针mid指向旋转数组中间位置的元素；指针right指向旋转数组最后一个元素。

      如果mid指向的元素>=left指向的元素，则mid位于递增子数组1，数组中最小元素位与中间元素的后面，将left指向mid后，缩小一半的寻找范围

      如果mid指向的元素<=right指向的元素，则mid位于递增子数组2，数组中最小元素位与中间元素的前面，将right指向mid后，缩小一半的寻找范围

      如果mid指向的元素==left指向的元素==right指向的元素，则无法确定mid位于哪个递增子数组，无法折半查找，只能顺序查找

二分查找结束标志：

      left指针始终指向递增子数组1，right指针始终指向递增子数组2，最终left指针指向递增子数组1的最后一个元素，right指针指向递增子数组2的第一个元素。当left+1=right时结束循环，right位置的元素即为最小元素。7  

3.code

#include <iostream>
#include <vector>
using namespace std;

class Solution {
public:
    int minNumberInRotateArray(vector<int> rotateArray)
    {
        // 空数组
        int size = rotateArray.size();							//数组长度
        if(size == 0)
        {
            return 0;
        }

        // 非空数组
        int left = 0;											//左指针
        int right = size - 1;									//右指针
        int mid = 0;											//中间指针（未旋转时直接输出rotateArray[0]）

        while(rotateArray[left] >= rotateArray[right])
        {
            // 循环结束标志(左右指针相邻)
            if(left+1 == right)
            {
                mid = right;
                break;
            }

            // 计算中间指针位置
            mid = left + (right - left) / 2;

            //特殊情况：如果无法确定中间元素是属于前面还是后面的递增子数组，只能顺序查找
            if(rotateArray[left] == rotateArray[right] && rotateArray[mid] == rotateArray[left]){
                return MinInOrder(rotateArray, left, right);
            }
            //中间元素位于前面的递增子数组，此时最小元素位于中间元素的后面
            if(rotateArray[mid] >= rotateArray[left]){
                left = mid;
            }
            //中间元素位于后面的递增子数组，此时最小元素位于中间元素的前面
            else{
                right = mid;
            }
        }
        return rotateArray[mid];
    }
private:
    //顺序寻找最小值
    int MinInOrder(vector<int> &num, int left, int right){
        int result = num[left];
        for(int i = left + 1; i <= right; i++){
            if(num[i] < result){
                result = num[i];
            }
        }
        return result;
    }
};
int main()
{
    Solution solution;
    vector<int> rotateArray = {4,5,1,2,3,4};
    cout<<solution.minNumberInRotateArray(rotateArray)<<endl;
    return 0;
}

4.复杂度

       时间复杂度O(logn)

5.测试用例

• 空指针
• 一个元素的数组
• 未旋转的数组
• 旋转的数组（无重复数字和有重复数字）