1.Boosting方法简介
Boosting是集成学习的一种,与之相对的就是Bagging。Boosting是一种将多个弱学习器组合在一起提升为一个强的学习器,多个弱学习器之间采用串行的方式进行连接(即上一个弱学习器的学习结果会对下一个学习器有影响),而Bagging则是采用并行的方式将多个弱学习器组合在一起。对于Boosting而言,主要存在两个核心问题
1.在每一轮学习弱学习器时,如何改变训练数据样本的权值?
由于Boosting是一种串行的方式连接这些弱分类器,那么上一轮的学习会对下一轮产生影响。我们通过上一轮的学习,可以将上一轮中被弱学习器分类错误的样本提高它的数据样本权重,而分类正确的样本我们减小它的数据样本权重,也就是在下一轮的学习中,我们更加重视对于分类错误样本的学习。
2.通过什么样的方式来将这些弱的学习器组合在一起呢?
采用加法模型将弱学习器进行加权的线性组合,如:对于训练效果比较好的弱学习器我们给与更多的权重,对于那些效果比较差的弱学习器我们给与的权重就小一些。
以上的这些关于样本权重的数值量化,以及学习器给与的权重的量化,对于具体的Boosting学习方法都会有各自的数学推导,这里不要太纠结。
常见的Boosting学习算法有:Adaboost、GBDT、XgBoost以及LightGBM(其实AdaBoost单独作为一支,GBDT就是一个一阶导数,Xgboost和LghtGBM就是二阶导数的,但LightGBM的运行速度会比Xgboost要快很多,但有时候Xgboost的效果要好一些)
2.AdaBoost
AdaBoost就是一个典型的Boosting的学习器。它的核心思想也就是来解决上文提到的两个问题(1.如何改变训练数据权重,2.通过什么方式将弱学习器组合在一起)
算法流程:

(1)初始化训练数据的权重分布(一开始也就是按照等权重,来分配样本权重1/n)

(2) 对于每一个弱分类器,假设弱分类器个数为M,则m = 1,2,...,M
(2.1) 使用权值分布Dm训练数据集,得到基分类器(也就是在Dm这样的一个分布下,我们去找一个使得分类误差最小的基分类器,因为你的误差计算离不开样本的权重,看下一步式子)
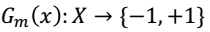
(2.2)计算Gm(x)在训练集上的分类误差率(I函数就是不等为1,相等为0)

(2.3)计算Gm(x)的系数,也就是计算核心问题中的2,关于每一个弱分类器的权重的给与(后面给出这个式子的推到过程,严格的数学推导)

(2.4)使用上面的分类误差em和权重am来更新数据权重分布,(本来是两个变量,我们先验的给了一个变量,然后推导另一个变量,在用推导的变量来更新先验的变量的值,是不是有点贝叶斯的感觉)
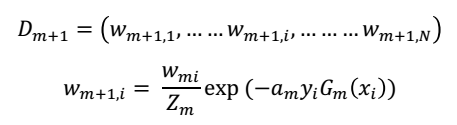
上式中,对于分类正确的样本,指数上的值为负的,那么指数结果小于1,也就是相对于上一轮的样本权重而言变小了,也就是弱化了分类正确样本。
对于分类错误的样本,指数上的值为正的,指数结果大于1,相对于上一轮的样本权重变大了,加强了对分类错误样本的重视程度。
这里面加了一点数学技巧,规范化因子Zm:(说白了机器学习就是一个概率问题,这样规范化之后,所有权重之后相加等于1,也防止出现权重两极化太大了)

(3)构建基本分类器的线性组合(基本上算是完成整个过程了)
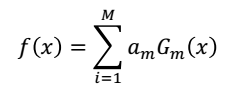
上式中,am也就是每一个基分类器的权重,仔细观察式子,可以看出am和em成反比,也就是说如果分类误差小,那么这个分类器的权重我就给多一点,反映出它的效果好。
得到最终的分类器
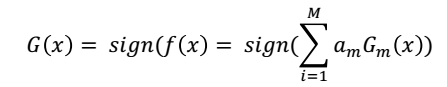
通过最终的分类效果。然后使用sign函数划分到-1,1上去
Adaboost数学推导:
首先损失函数选用指数函数,其形式为:
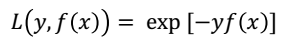
假设经过m-1轮迭代之后,得到的学习器为:
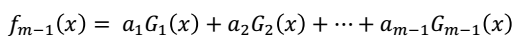
那么,在第m轮是,得到的学习器为:
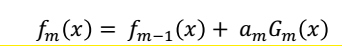
第m轮迭代的目标是这一轮得到的系数和基分类器在训练集上的损失函数最小,即:
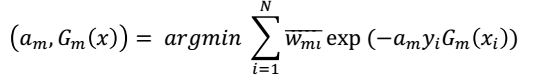
其中,对于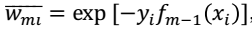 ,也就是我们对于样本进行加权时的分子项,没有进行归一化处理。仔细看
,也就是我们对于样本进行加权时的分子项,没有进行归一化处理。仔细看
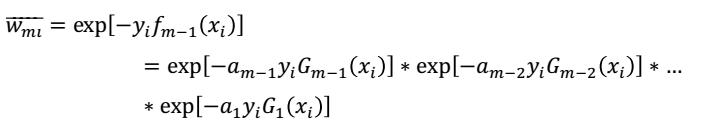
对于上式,我们首先求解Gm,当然这个比较好求,在Dm-1的权重分布下,我们求解出使得损失最小化的弱学习器。
对于am的求解

上式对a求导等于0,即可得:
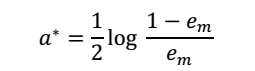
看到没,这就是之前的a更新的数学推导