c语言数字图像处理（十）：阈值处理

定义

全局阈值处理

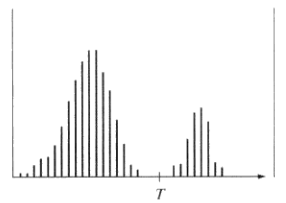
假设某一副灰度图有如下的直方图，该图像由暗色背景下的较亮物体组成，从背景中提取这一物体时，将阈值T作为分割点，分割后的图像g(x, y)由下述公式给出，称为全局阈值处理

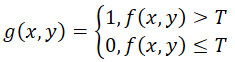
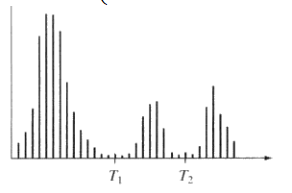
多阈值处理

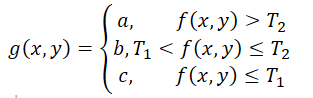
本文仅完成全局阈值处理的算法实现

基本全局阈值处理方法

1. 为全局阈值T选择一个初始的估计值

2. 用T分割图像，产生两组像素：G1由大于T的像素组成，G2由小于T的像素组成

3. 对G1和G2的像素分别计算平均灰度值m1和m2

4. 计算新的阈值T = 1/2 * (m1 + m2)

5. 重复步骤2-4，直到连续迭代中的T值差小于一个预定义的参数ΔT

算法实现

void threshold(short** in_array, short** out_array, long height, long width, int delt_t)
{
    double T = 0xff / 2.0;
    double m1 = 0.0, m2 = 0.0;
    int m1_num = 0, m2_num = 0;

    while(dabs(T, 0.5*(m1 + m2)) > delt_t){
        T = 0.5 * (m1 + m2);
        m1 = 0.0;
        m2 = 0.0;
        m1_num = 0;
        m2_num = 0;

        for (int i = 0; i < height; i++){
            for (int j = 0; j < width; j++){
                if (in_array[i][j] <= T){
                    m1 += in_array[i][j];
                    m1_num++;
                }
                else{
                    m2 += in_array[i][j];
                    m2_num++;
                }            
            }
        }
        if (m1_num != 0)
            m1 /= m1_num;
        if (m2_num != 0)
            m2 /= m2_num;
        printf("%lf
", T);
    }
    for (int i = 0; i < height; i++){
        for (int j = 0; j < width; j++){
            if (in_array[i][j] <= T)
                out_array[i][j] = 0xff;
            else
                out_array[i][j] = 0x00;
        }
    }
}

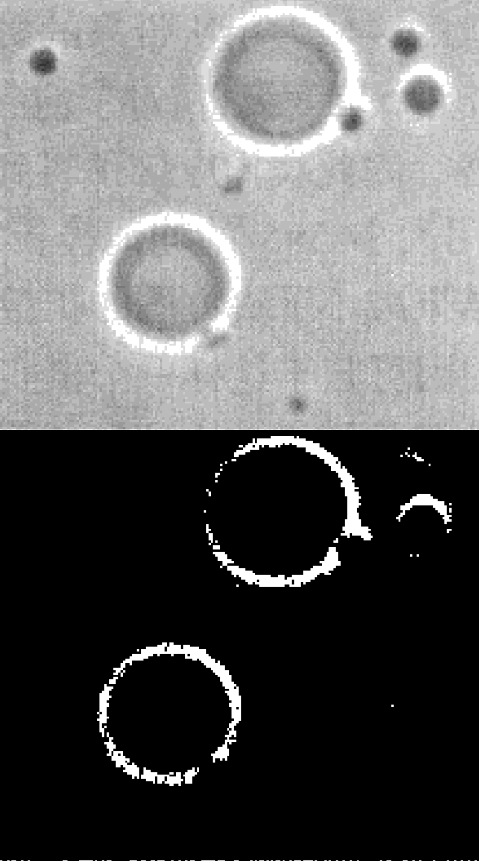
测试结果

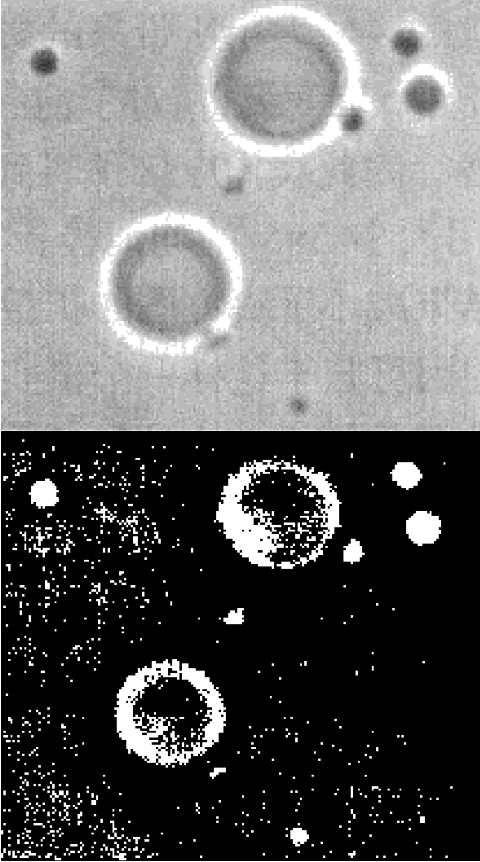
 从实验结果看出，第二组阈值处理的效果并不好，因此考虑更优的算法实现

Otsu方法进行最佳全局阈值处理

阈值处理可视为一种统计决策理论问题，其目的是在把像素分配给两个或多个组的过程中引入的平均误差最小。这一问题有个闭合形式的解，称为贝叶斯决策规则。

Otsu方法在类间方差最大的情况下是最佳的

算法执行流程

代码实现

double dabs(double a, double b)
{
    if (a < b)
        return b-a;
    else
        return a-b;
}

void calculate_histogram(long height, long width, short **image, unsigned long histogram[])
{
    short k;
    for(int i=0; i < height; i++){
        for(int j=0; j < width; j++){
            k = image[i][j];
            histogram[k] = histogram[k] + 1;
        }
    }
}

void calculate_pi(long height, long width, unsigned long histogram[], double pi[])
{
    for (int i = 0; i < GRAY_LEVELS; ++i){
        pi[i] = (double)histogram[i] / (double)(height * width);
    }
}

double p1(int k, double pi[])
{
    double sum = 0.0;

    for (int i = 0; i <= k; i++){
        sum += pi[i];
    }

    return sum;
}

double m(int k, double pi[])
{
    double sum = 0.0;

    for (int i = 0; i <= k; i++){
        sum += i * pi[i];
    }

    return sum;
}

double calculate_sigma(int k, double mg, double pi[])
{
    double p1k = p1(k, pi);
    double mk = m(k, pi);

    if (p1k < 1e-10 || (1 - p1k) < 1e-10)
        return 0.0;
    else
        return pow(mg * p1k - mk, 2) / (p1k * (1 - p1k));
}

void otsu(short** in_array, short** out_array, long height, long width)
{
    unsigned long histogram[GRAY_LEVELS] = {};
    double pi[GRAY_LEVELS] = {};
    double sigma[GRAY_LEVELS] = {};
    double mg;
    short max_count = 0;
    short k = 0;
    double max_value = 0.0;
    double k_star;

    calculate_histogram(height, width, in_array, histogram);
    calculate_pi(height, width, histogram, pi);
    mg = m(GRAY_LEVELS-1, pi);

    for (int i = 0; i < GRAY_LEVELS; i++)
        sigma[i] = calculate_sigma(i, mg, pi);

    max_value = sigma[0];
    max_count = 1;
    k = 0;
    for (int i = 1; i < GRAY_LEVELS; i++){
        if (dabs(sigma[i], max_value) < 1e-10){
            k += i;
            max_count++;
        }
        else if (sigma[i] > max_value){
            max_value = sigma[i];
            max_count = 1;
            k = i;
        }
    }
    k_star = k / max_count;

    printf("%lf
", k_star);
    for (int i = 0; i < height; i++){
        for (int j = 0; j < width; j++){
            if (in_array[i][j] <= k_star)
                out_array[i][j] = 0x00;
            else
                out_array[i][j] = 0xff;
        }
    }
}

结果